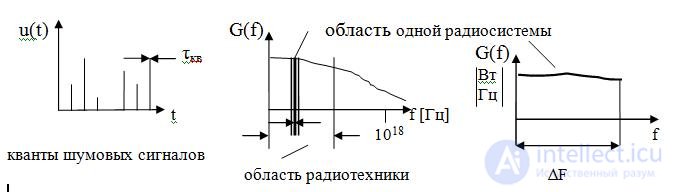
For objects conducting current include metals and semiconductors. In addition, there are a number of media with a different type of conductivity, such as ionic, plasma, etc. These objects and media are sources of electrical noise with a thermal cause. So, in metals, the cause of electrical noise is the spontaneous movement of electrons. In this case, a Poisson flux of ultrahigh-time electrical quanta τ q ≡ 10-18 s is formed , as shown in Fig. 1.1.
rice 1.2. Thermal Electrical Noise Characteristics
The spectrum of noise electrical quanta extends far beyond the area where radio engineering devices operate. With a total noise power p ∑ [W], the spectral density of the power of the noise flux g ( f ) is measured in W / Hz and can be calculated using the Boltzmann constant k b and the conditional temperature in Kelvin degrees T c . Accordingly, the total power is calculated by integrating the power spectral density within the entire noise band, and the power at the output of the radio engineering device - within their frequency bandwidth ∆ F.
G ( f ) = k b T to k b = 1.38 10 -23 T to T to = 273 + t o C
∞
p ∑ = ∫ G ( f ) df , p w = ∫ G ( f ) df (one)
about ∆ F
where the conditional coefficient of the radio device is equal to 1, k b has the dimension [W / Hz Grad].
Often, within one radio device, the envelope of the noise spectrum changes little. Then they say that this is “white noise”, and the spectral density of the noise is designated as n W 2 = G W ( f ). The box is marked in order to emphasize that this is a scale of capacities. It is known that engineers using a spectrum analyzer, on the monitor screen see the spectrum on a voltage scale. Then the same indicator can be written as n sh , and the voltage spectrum is like U ( f ) [ B / Hz]. We remind that on the conditional load 1 Ohm, power and voltage are related as follows: p = u eff 2 = σ u 2 . Here u ef Is the effective stress value, and σ u 2 - process variance, if we are talking about stochastic processes.


Comments
To leave a comment
Radio Engineering Systems
Terms: Radio Engineering Systems