Radar equation

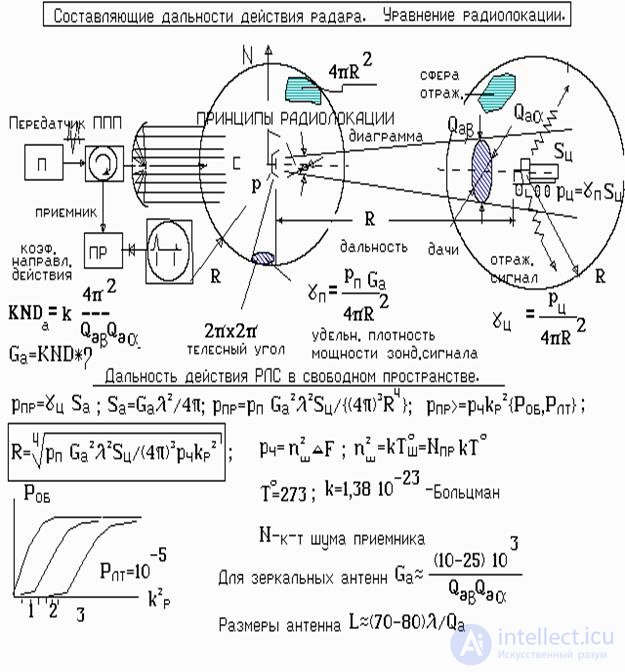
The transmitter radiates into space some microwave power _pp . If the antenna is omnipotent , then all power will be distributed over a sphere of radius R. The power coming to 1 m ^{2 the} area of ​​the sphere is called the power flux density g _{p .} If the antenna mirror is positioned at the radiation point, the power flux density will increase by the antenna gain G _a .

The target, moving at a distance R from the radar, intercepts some power p _{c .} Its value is equal to the flux density multiplied by the EPR of the target s .

In turn, the target radiates the intercepted power diffuse in all directions of the space , including in the direction of the radar. Density of signal power from the target at the radar antenna g _C calculated similarly to g _p . Only that part of the power that is intercepted by the antenna area S a is _received. But the area of ​​the antenna is related to its gain coefficient G _a and long wave l . Taking into account the above considerations, the power of the reflected signal at the input of the receiver can be calculated . The final form-la will be the first form of the radar equation.

The first form of the radar equation allows you to calculate the power of the reflected signal . However, it does not make it possible to calculate the range of the radar, since it does not take into account the power of the intrinsic noise of the receiving path. From lecture 2.4. It is known that the reflected signal can be detected with certain probabilities of correct detection of P _о and false alarm P _LT . To calculate the need to know the power of noise and signals and the level of the threshold in the automatic detector. As was shown earlier, it is enough to know their values ​​at the receiver input. How to calculate the level of noise brought to the receiver input is given in Lecture 2.3. The calculated noise power at the receiver input can be interpreted as its “technical” sensitivity r _h .

The specific calculation of the automatic detector is not always necessary. To simplify the calculation , the concept of a generic receiver with an auto detector is introduced, where the threshold level is optimized for given detection probabilities and false alarms. For given values ​​of P _lt , curves of dependences of P _on on the signal-to-noise ratio are plotted . This ratio is often called the “discriminability coefficient” to _p The resulting curve family is called the “performance” of the generic receiver. For given P _about and P _Lt and curves generalized receiver, you can find the coefficient of distinction to _r .

now we We took into account the receiver's own noise at the input and know that the signal must exceed them by k _times , so that it can be detected with given probabilities.

Solving the first radar equation with respect to R , and taking into account the above considerations , one can obtain the second form of the radar equation for calculating the radar range.