Lecture
How does a person differ from an animal? “Man is a decision making animal” (I.Bross). A decision is a choice, it is a person’s awareness that he can perform actions D 1 , D 2 , ..., D n , a comparison of these possibilities and a conclusion about the expediency of performing precisely actions D i and not others.
The use of mathematical quantitative methods to justify decisions in all areas of targeted human activity is called operations research.
The need for decision making is as old as humanity itself (the hunt for a mammoth).
In everyday life, we constantly make decisions. But, as a rule, justification, optimization of these solutions is not required.
More complex decisions made during various technological operations. This is where an assessment of the consequences of the actions that science, called “operations research” (IO), studies is required.
Historical excursion.
In 1938, a twenty-five year old professor at Leningrad University, Leonid Vitalyevich Kantorovich (1912 - 1986), was tasked with how best to distribute the work of 8 plywood trust machines, provided that the performance of each machine is known for each of the five types of materials being processed? The scientist found a general method for solving this problem, which was called “linear programming” (LP).
In 1975, together with T. Kupmans (USA), L. Kantorovich was awarded the Nobel Prize in economics for his contribution to the theory of optimizing the distribution of resources, and in 1986 - the Big Silver Medal of the Society for Operations Research for the role of pioneer in linear programming.
On the other hand, the methods of LP and other mathematical methods were used and simultaneously developed during the Second World War to plan military transfers and military operations. Special units were established in the USA and Canada to analyze military operations. In 1938, the term “operation research” was introduced in Great Britain as a characteristic of the type of activity of a special group that solves the problem of optimal use of radars in the general defense system.
Later, the principles and methods of IO began to be applied in the industrial and financial sphere, trade, transport, and communications. The scope of operational research, the range of tasks and methods of new science expanded.
There was a need for training of specialists in operations research - tellers. For the first time in the leading universities of the USA and England, the systematic teaching of the course of IO began.
The basic concept and principles of IO.
In the broad sense of the word, an operation is any purposeful action. The nature of operations can be different - it can be military actions, production processes, commercial events, administrative decisions, etc., etc., etc., etc. ... What is interesting is that these operations (completely dissimilar in nature ) can be described by the same mathematical models (!), moreover, the analysis of these models makes it possible to better understand the essence of a particular phenomenon and even predict its further development. The world, as it turned out, is built unusually compact (in the information sense), since the same information scheme is implemented in a variety of physical (and not only physical) manifestations. This is called "model isomorphism."
If it were not for the isomorphism of models, for each specific situation it would be necessary to look for its own, unique method of solution, and IO as a scientific direction would not have been formed. Fortunately, the situation is different; due to the presence of common patterns in the development of various systems, it is possible to study them by mathematical methods. IO as a mathematical tool that supports the decision-making process in various areas of human activity, as a set of tools to provide the decision maker with the necessary quantitative information obtained by scientific methods, was formed at the junction of mathematics and various socio-economic disciplines; representatives of various fields of science have contributed to its development.
We will call the operation any event (set of actions), united by a single plan and directed towards the achievement of some goal. An operation is always a managed event, i.e. it depends on us how to choose the parameters characterizing its course. The purpose of the operation is considered given and, as a rule, the only one.
The combination of those individuals and automata who in this operation are striving towards the goal set is called the operating party. Usually, there are individuals or natural forces in the operation whose behavior is by no means aimed at achieving the goal of the operation (football match: team, coaches, fans, active opponent, judges).
The operating party is the subject of the operation, and the operation itself is the object. To the operating side belongs and the investigator of the operation. It acts in the interests of the operating party, and its task is to find a way for the capabilities of the operating party to achieve the goal.
The investigator of the operation, as a rule, does not make decisions on the choice of methods of action, but only helps in this operating side. Thus, despite the researcher’s belonging to the operating side, he occupies a definite place in it, exploring the operation as a whole, but being often deprived of all the fullness of information about the operation and not making final decisions.
To achieve the goal, the operating side has at its disposal a certain stock of active funds, using, and, as a rule, spending that, it achieves a goal. This stock is called a resource.
A resource may be material resources, energy, information, finance, labor, a computer resource.
Modes of action, i.e. methods of using active funds will be called the strategies of the operating side.
The results of operations to achieve goals depend, on the one hand, with a given amount of active funds on the choice of strategies, i.e. from factors at the disposal of the operating party. Such factors are called controlled. However, the results may also depend on factors that are not controlled by the operating party. These factors usually form what is called the setting for the operation.
Any choice of strategy, in the form of factors depending on us, is called a decision. Optimal solutions are solutions that, for one reason or another, are preferable to others. Decision making itself is beyond the scope of the Oncological Institute and is the function of a person or group of persons who have been granted the right of final choice and who are responsible for making a decision (the decision maker is the decision maker).
Exploring the operation, we strive to make it the most effective. The effectiveness of the operation is understood as the degree of its fitness to achieve the goal. To compare the effectiveness of different solutions, you need to have a quantitative measure of efficiency. The degree of compliance of the course of the operation with the goal is characterized by the criterion of efficiency (objective function) W. When choosing solutions, we prefer one that turns W into a maximum (or a minimum). For definiteness, we assume that we minimize the criterion.
The desire to increase the efficiency criterion is a mathematical description of the purpose of the operation: Wmax.
Stages of operations research.
In the task of research operations there are always stages:
Stage 1.
Construction of the model, that is, the formalization of the process or phenomenon under study. It boils down to describing the process in the language of mathematics. Using the same model, various operations can be studied. The mathematical model should reflect the most important features of the phenomenon, all the essential factors on which the success of the operation depends. Since an operation is a purposeful action, the operation model must be a combination of:
- the subject (the operating party), formulating the purpose of the operation;
- stock of active funds (resources) for the operation;
- a set of strategies, that is, how to use these resources;
- the criterion, that is, the method of comparing different strategies pursuing the achievement of a goal.
Do not confuse purpose and criterion. Building a model is a certain art, and the experience in it comes gradually. The originator of the model faces two dangers:
1. get bogged down in details (“not seeing the forest because of the trees”);
2. too coarsen the phenomenon ("throw out the child with water").
The quality of the decision is greatly influenced by the certainty of our knowledge of the model. Any decision made under conditions of uncertainty is worse than a decision made under previously known conditions. A bad or good decision must be made. Our business is to make this decision more reasonable.
T. Saati said not without irony: “IO is an art of giving bad answers to practical questions, to which even worse answers are given by other methods.”
The set of mathematical models of IO can be divided into two groups.
The first group includes deterministic models: LP, integer programming, graph theory, flows in networks, geometric programming, nonlinear programming, programming for the case of large-dimension problems, optimal control theory.
The second group includes stochastic models: random processes, queuing theory, utility theory, control decision analysis, game theory, search theory, simulation modeling, and dynamic programming.
Stage 2.
Description of the operation - statement of the problem. The task of the investigator of the operation at this stage is to analyze the uncertainties and limitations, to formulate, ultimately, some optimization task:
W (x) max, xG,
x is the vector of parameters (factors);
G is a set that can have an arbitrarily complex nature.
Thus, after this stage, the task of the IO is treated as an optimization problem. To solve it, a number of mathematical methods have been developed: linear, nonlinear, dynamic programming, etc. Note that the word “programming” is bad here, but the well-established translation of the word programming is programming, planning (progress), and has no relation to the compilation of computer programs. Language optimization is not the only possible (game theory).
Stage 3.
Solving an optimization problem. Of great importance at this stage is the human factor.
Stage 4.
Check the adequacy of the model.
Stage 5.
The implementation of the solution.
The principle of guaranteed results.
We have already said that there are uncontrollable factors in the operation.
With a given performance criterion, the evaluation of strategies (options) and their selection should occur on the basis of obtaining a guaranteed value of the efficiency criterion in an uncontrolled (uncontrolled) environment of the operation. This means that the investigator of the operation should be guided by the worst values of uncontrolled factors. Such behavior is natural if only because it does not have the right to take a decision that puts the entire operating party at risk. Moreover, the operating party usually does not grant such rights to the investigator.
When conducting an EI, the researcher must be careful. If, however, this caution leads in some sense to unsatisfactory results, he informs the operating side, which will make a decision, which in turn may be risky. The operating party takes the risk quite often, but this should not be done independently by the investigator of the operation.
Multi-criteria task research operations.
Unfortunately, when planning complex operations, their effectiveness, as a rule, cannot be fully characterized by one criterion W. These tasks of the Oncological Institute are called multicriteria. (Production - output, incomemax, costs, costmin). Typical for a large-scale task is multicriteriality - the presence of a number of quantitative indicators W 1 , W 2 , ..., W n , some of which should be turned into a minimum, and others into a maximum (“the wolves are fed and the sheep are safe”).
Frankly, it is impossible to carry out such an operation. The phrase “achieve maximum results at minimum cost” is an unscientific concept.
There are methods for converting a multicriteria task to a single-criterion (the so-called convolution of criteria). Often such a generalized criterion has the form of a fraction, in the numerator of which are all the indicators that it is desirable to maximize, and in the denominator - to minimize (income, production - in the numerator; consumption, costs - in the denominator). This method has a big disadvantage: it is based on the assumption that the lack of one indicator can be compensated at the expense of another (price / quality). As a rule, this is unfair.
The construction of any IO task is always associated with the need to fulfill two essentially contradictory requirements:
a) to reflect the studied phenomena as accurately as possible (the adequacy of the model);
b) to build a fairly simple mathematical model that allows you to solve the original problem and get the results.
As a rule, this is achieved within the framework of the operating party through the cooperation of the operations researcher and the decision maker.
Let there be a multicriteria task of the Oncological Institute with criteria W 1 , W 2 , ..., W n , which should be maximized. Suppose that in the set of all possible solutions there are two solutions x 1 and x 2 such that all criteria W 1 , W 2 , ..., W n for the first solution are greater than or equal to the corresponding criteria of the second solution: W i (x 1 ) ≥ W i (x 2 ), i =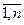 
, (*) and at least one of many is really more. Obviously, as part of the solution set X, there is no point in preserving the solution x 2 . It is supplanted or dominated by solution x 1 . You can discard the solution x 2 and go to the consideration of the remaining solutions by comparing all criteria. Throwing away all unfavorable solutions, we will leave only those that satisfy the inequality. As a result, we obtain the set of additive solutions X * or the Pareto set (1904) (Wilfredo Pareto, 1843-1923). This set is characterized by the fact that for all its elements there is no dominant solution. The Pareto set is also called the set of unimproved alternatives, the negotiating set, the set of compromises. Graphically, for two criteria, the Pareto set can be represented as follows:
The Pareto set (set of additive solutions) belong only to the points on the right upper (north-east) boundary.
The Pareto principle in the theory of solutions is that you only need to choose the vector X as the solution, which belongs to the Pareto set. The Pareto principle does not single out a single solution; it only narrows down the many alternatives. Further, already within the additive set, the decision maker seeks a compromise.
The upper section of the Pareto set R p is empty. For elements of the Pareto set, one of the alternatives cannot be improved without deteriorating the other.
If inequality holds
W i (x 1 )> W i (x 2 ), i = ,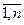
then it is similarly possible to form a set of weakly effective solutions or a set optimal for Slater, solutions which cannot be improved by all criteria at once.
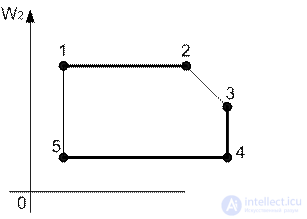
Points 1,2,3,4 belong to Slater's set. Obviously, the Pareto set is a subset of the Slater set: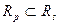 
Comments
To leave a comment
Mathematical methods of research operations. The theory of games and schedules.
Terms: Mathematical methods of research operations. The theory of games and schedules.