Game evaluation function

The evaluation function returns a prediction of the expected utility of the game from this particular position, by analogy with the way the heuristic functions described in return the predicted value of the distance to the target. The idea of ​​such an "appraiser" at the time when Shannon offered to use it was not new. For centuries, chess players (and fans of other games) have developed ways to make judgments about the value of a position, because people are even more limited in the amount of search that can be performed by them than computer programs.

It should be obvious that the performance of any gaming program depends on the quality of the evaluation function used. An inaccurate assessment function will lead the agent to positions that are losing. Therefore, an important question arises - how exactly should good evaluation functions be designed?

First, the evaluation function must order the terminal states in the same way as the real utility function; otherwise, the agent using it can choose non-optimal moves, even having the ability to calculate all the moves until the end of the game. Secondly, the calculations should not take too much time! (In the evaluation function, we could call Minimax-Decision as a procedure and calculate the exact cost of this position, but this would call into question what we are striving for - time saving.) Thirdly, for non-terminal states, the values ​​of this evaluation function must be strictly correlated with the actual chances of winning.

The expression "odds of winning" at first glance may seem strange. In the end, chess is not a game with elements of chance: it certainly knows the current state and does not need to draw lots to determine the next move. But if the search should stop in non-terminal states, then this algorithm will necessarily have uncertainty about the final outcomes for these states. Uncertainty of this kind is caused by computational rather than informational constraints. Because of the limited amount of computation that is allowed to be performed in the evaluation function for a given specific state, the best thing it can do is to accept some assumption regarding the final result.

Consider this idea a little more specifically. The evaluation functions most often act on the principle of calculating various characteristics of a given state, for example, in chess, one of such characteristics is the number of pawns belonging to each side. These characteristics, taken together, define different categories, or equivalence classes of states: states from each category have the same values ​​for all their characteristics.

Generally speaking, any particular category includes some conditions that lead to victory, draw or defeat. The evaluation function does not allow one to determine what certain states are, but is capable of returning a single value that reflects the percentage of these states in each result.

For example, suppose the experience obtained shows that 72% of the states encountered in this category go to victory (utility +1); 20% to defeat (-1) and 8% to a draw (0). In this case, an acceptable estimate for the states of this category is the weighted average, or the waiting value: (0.72x + 1) + (0.20x - 1) + (0.08x0) = 0.52

In principle, the expected value can be determined for each category, resulting in a final evaluation function applicable to any state. As in the case of terminal states, the evaluation function is not required to return the actual expected values, provided that the ordering of the states remains the same.

In practice, this kind of analysis requires taking into account too many categories and therefore accumulating too much experience in order to evaluate all the probabilities of gain. Instead, in the majority of functions, estimates are calculated for individual numerically presented contribution values ​​depending on each characteristic, after which these values ​​are combined to find the total value.

For example, in chess books for beginners, you can find approximate estimates of the cost of material for each piece: for example, such that a pawn has a value of 1, a knight or an bishop is 3, a rook is 5, and a queen is 9. Other characteristics such as "good The pawn structure and the king’s security can be assessed as equal to, say, half the value of a pawn. After that, the cost of such characteristics simply add up to obtain an estimate of the position. A reliable advantage, equivalent to the value of a pawn, is regarded as a significant probability of winning, and a reliable advantage of three pawns should almost certainly ensure victory, as shown in the figure.

In mathematics, an evaluation function of this type is called a weighted linear function, since it can be represented as follows:

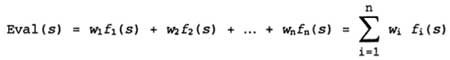where each coefficient w _i is a weight, and each function f _i evaluates some position characteristic. In chess, the function f _i can determine the number of pieces of each type on the board, and the coefficient w _i estimate the values ​​of these pieces A per pawn, 3 per bishop, etc.).

Two slightly different chess positions: Black has an advantage of one knight and two pawns and must win the game (a); Black loses after White takes the queen (b)

At first glance, the method of calculating the sum of the characteristics of the characteristics may seem acceptable, but in reality it is based on the very radical assumption that the contribution of each characteristic does not depend on the value of the other characteristics. For example, by assigning cost 3 to an elephant, we ignore the fact that elephants become more powerful at the end of the game when they have a large amount of room to maneuver. For this reason, non-linear combinations of characteristics are also used in modern programs for chess and other games. For example, a pair of elephants can cost a little more than double the cost of an elephant, and an elephant costs a little more at the end of the game than at the beginning.

The attentive reader should have noticed that all these characteristics and weights are not part of the chess rules! They were developed over the centuries based on the experience of people playing chess. The use of these characteristics and weights on the basis of the described linear form of estimation allows us to achieve the best approximation with respect to the true ordering of states in terms of value. In particular, experience shows that a reliable material advantage of more than one point in all likelihood leads to gain, all other things being equal; a three point advantage is enough for almost unconditional victory. In such games, where the experience of the specified type is absent, the weights of the evaluation function can be obtained using machine learning methods. It is encouraging that the application of these methods to chess has confirmed that the bishop really has a value approximately equal to three pawns.