By analogy with minimax values, an obvious approach to using the expected minimax values is to stop the search at some point and apply the evaluation function to each sheet. At first glance, it may seem that the evaluation functions for such games as backgammon should be completely similar to the evaluation functions for chess, since all they need to do is to assign higher marks to better positions. But in reality, the presence of drawing lots means that a more thorough analysis of the meaning of such estimated values is required.
The figure shows what happens in games with elements of randomness — when using the evaluation function, which assigns the values [1,2,3,4] to leaves, the best move is A
1 and if the values are assigned [1,20,30,400], the best becomes move A
2 . Therefore, the program behaves completely differently if changes are made to the scale of some estimated values! As it turned out, such sensitivity to change of the scale can be avoided, provided that the evaluation function is a positive linear transformation of the probability of winning from a certain position (or, more generally, the expected utility of this position). This is an important and common property of situations associated with the presence of uncertainty.
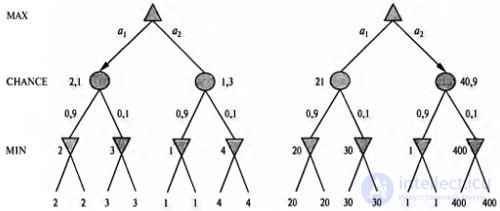 |
| An example of the fact that as a result of the transformation of the estimated values of the leaves, at which the ordering of these values does not change, the best move becomes different |

Comments
To leave a comment
Mathematical methods of research operations. The theory of games and schedules.
Terms: Mathematical methods of research operations. The theory of games and schedules.