Alpha beta cut

In the case of a minimax search, the problem is that the number of game states that should be investigated during the search process depends exponentially on the number of moves. Unfortunately, such an exponential relationship cannot be eliminated, but in fact there is the possibility of reducing it by half. The whole secret is that the calculation of the correct minimax solution is possible without checking each node in the game tree. This means that you can borrow the idea of ​​clipping to exclude large parts of the tree from consideration.

The specific method discussed in this chapter is called alpha-beta pruning. Being applied to a standard minimax tree, this method returns the same moves that the minimax method would return, but cuts off branches that are most likely incapable of affecting the final decision. Again we will consider a game tree with two half-moves and once again we will carry out the calculation of the optimal solution, this time paying special attention to what is known at each stage of this process. Explanations for these stages of calculation are shown in the figure. The result is that the minimax solution can be revealed without even starting to calculate the values ​​of two leaf nodes.

This approach can also be viewed from a different angle - as a simplification of the formula for obtaining the minimax Minimax-Value value. Suppose that two successors of node C in fig. 6.4, not yet processed in the calculation process, have the values ​​x and y, and assume that z is the minimum value among x and y. In this case, the value of the root node can be found as follows:

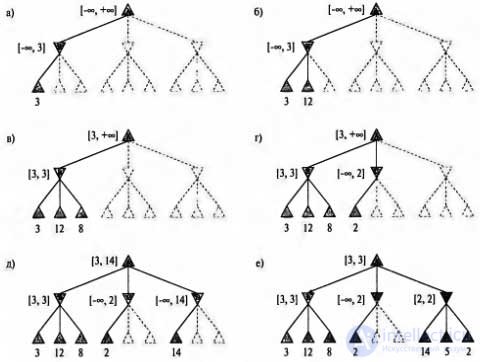
In other words, the value of the root node, and hence the minimax solution, does not depend on the values ​​of the cut-off leaf nodes x and y. Alpha-beta pruning can be applied to trees of any depth; moreover, it is often possible to cut off entire subtrees, and not just leaves. The general principle is as follows: consider a node l, located somewhere in the tree, that a participant in the game from the observer’s side (let's call him the Player) has the opportunity to choose the move leading to this node. But if the Player has the best choice t either at the parent node of the node n, or at any other choice point,
located even higher in the tree, then with node n will never be achieved in a game that takes place in reality. Therefore, after obtaining sufficient information about the node n (by examining some of its descendants) in order to arrive at this conclusion with complete confidence, it is possible to cut it off.

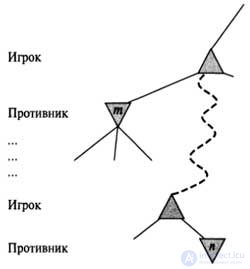
Fig. 6.5. Alpha Beta Clipping: The General Case. If for Player a node m is better than n, then a node n will never occur in the game.

Recall that the minimax search is carried out in depth, so at any time it is enough to consider the nodes along the only path in the tree. The alpha-beta cut-off algorithm got its name from the following two parameters, which represent the limits in the reserved values ​​present at all nodes along this path:

• a = the value of the best option (i.e. the option with the highest value), which has so far been found at any point of choice along the path for the player MAX;
• P = the value of the best option (i.e. the option with the lowest value) that has been found so far at any point of choice along the path for the player MIN.

The alpha-beta search algorithm, in the course of its work, updates the values ​​of a and P, and also cuts off the remaining branches in the node (that is, stops recursive calls) as soon as it becomes known that the value of the current node is worse than the current value of a or P for player MAX or MIN respectively. The full algorithm is shown in the listing. We recommend the reader to follow his behavior in relation to the tree shown in the figure.

---

Alpha beta search algorithm. Note that the procedures used here remain the same as the Minimax algorithm procedures shown in the listing, with the exception of two lines entered both in the Min-Value procedure and in the Max-Value that accompany the values ​​of wasps and C ( and also perform appropriate actions for the further transfer of these parameters)

function Alpha-Beta-Search (state) returns action action
inputs: state, current state of the game
v <- Max-Value (state, - “>, + oo)
Return action action from the set of Successors (state) with the value v

function Max-Value (state, a, C) returns utility value
inputs: state, current state of the game
a, the value of the best alternative for player MAX along
state paths
C, the value of the best alternative for the player MIN along
state paths
if Terminal-Test (state) then return Utility (state)
v <- -oo
for a, s in successors (state) do
v <- Max (y, Min-Value (s, a, C))
if v> C then return v
a <- max (a, v)
return v

function Min-Value (state, a, | 3) returns utility value
inputs: state, current state of the game
a, the value of the best alternative for player MAX along
state paths
C, the value of the best alternative for the player MIN along
state paths
if Terminal-Test (state) then return Utility (state)
for a, s in successors (state) do
v if v then return v
P return v

---

The effectiveness of the alpha-beta clipping algorithm is highly dependent on the order in which the successors are tested. For example, in the figure, it would not be possible to cut off any successors of the node d at all, since the worst successors would be formed first (from the point of view of the MIN player). And if, first of all, a third successor was formed, but there would be an opportunity to cut off the other two. Based on this, we can conclude that it makes sense to strive to investigate, first of all, such successors who, in all likelihood, may become the best.

If we assume that this can be done, it turns out that in the alpha-beta-clipping algorithm, to determine the best move, it is enough to examine only 0 (lf / 2) nodes, and not O (If1) nodes, as when using the minimax algorithm. This means that the effective branching ratio becomes equal to - \ / 5, and not b; for example, for chess it is equal to b, not 35. In other words, during the same time, the alpha-beta search allows you to look into the game tree approximately two times farther than the minimax search. And if the study of successors occurs in a random order, and not according to the principle of first choice of the best options, then at moderate values ​​of L, the total number of nodes studied will be approximately 0 (L3TF). In the case of chess, the use of a fairly simple ordering function (for example, one in which the capture of pieces is first considered, then the threats, then the moves ahead, and then the moves back) allows you to stay within the limits not exceeding twice the value
a result of 0 (if / 2), which can be obtained in the best case. The addition of the dynamic moves ordering schemes, in particular, those in which the moves designated as the best at the previous stage are checked first of all, make it possible to come very close to this theoretical limit.

As noted, the presence of recurring states in the search tree can cause an exponential increase in the search cost. In games, repetitive states are often found due to the occurrence of transpositions — various permutations of sequences of moves that end in the same position. For example, if White has at his disposal the move al5 on which Black can respond with the move Bx, as well as one more unrelated move a2 on the other side of the board, which can be answered with b2, then both sequences, [alfblra2fb2] and [ a1, b2, a2, b1], end in the same position (as well as permutations starting with a2). Therefore, it is advisable to maintain an estimate of each specific position in the hash table when it first appears, so that you do not have to calculate it again during subsequent occurrences. By tradition, a hash table with previously encountered positions is called a transposition table; it is essentially identical to the closed list in the Graph-Search algorithm.

Using a transposition table can have an extremely effective impact, which is sometimes expressed in doubling the achievable depth of search in chess. On the other hand, if it is possible to calculate estimates at a speed of several million nodes per second, then there is almost no point in storing data about all these nodes in the transposition table. Various strategies have been tried to select the most valuable of these nodes.