Lecture
Example. Playing with two fingers Morra.
Two players simultaneously show one or two fingers and call the number one or two, guessing the number of fingers shown by the opponent. If both guessed right, the game ends in a draw, the winnings of both players are zero, if both didn't guess, is also a draw. If only one player guessed right, the guess player gets a win equal to the total number of fingers shown. Each has four strategies:
1) {1,1}; 2) {1,2}; 3) {2,1}; 4) {2,2}.
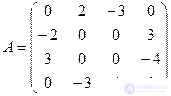
Example. War game.
There are two positions and two opponents - the colonel and the general. The colonel has 4 regiments, the general - 3. Everyone wants to take a position. Positions taken are valued by one. Everyone can send a whole number of regiments to any position or not send at all. The position is considered to be occupied by those who sent more regiments to it and the gain is one plus the number of enemy regiments who have not taken the position. If the position has an equal number of regiments, the gain is zero. The total gain is considered in two positions. Winning one is considered losing the other.
The colonel has such pure strategies:
1. {4.0}; 2. {0,4}; 3. {3.1}; 4. {1,3}; 5. {2,2}
The general has pure strategies:
1. {3.0}; 2. {0,3}; 3. {2,1}; 4. {1,2}
Matrix game:
Example.
Two companies A and B are selling flu medicine.
Company A advertises products:
- on the radio (A 1 )
- on television (A 2 )
- in newspapers (A 3 ).
Company B also operates (B 1 , B 2 , B 3 ), and in addition, they send out promotional brochures (B 4 ).
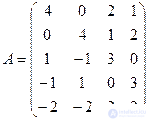
Each of the companies by their actions can win over a certain percentage of the clients of a competing company. This is set by the game matrix:
In 1 | In 2 | At 3 | At 4 | Line minimums | |
A 1 | eight | -2 | 9 | -3 | -3 |
A 2 | 6 | five | 6 | eight | 5Maximin |
A 3 | -2 | four | -9 | five | -9 |
Column maxima | eight | 5Minimax | 9 | eight |
(Games with a saddle point of 5%)
Mixed strategies.
A significant proportion of matrix games are games without a saddle point, in which the lower price of the game  strictly less than the top price
strictly less than the top price 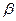 . . If such a game consists of only one game, that is, each player makes a move, then caution of behavior motivates player A to choose one of his maximin strategies, and player B one of his minimax strategies. Then player A ensures his gain, no less than
. . If such a game consists of only one game, that is, each player makes a move, then caution of behavior motivates player A to choose one of his maximin strategies, and player B one of his minimax strategies. Then player A ensures his gain, no less than  , and player B ensures that player A’s winnings will be no more than
, and player B ensures that player A’s winnings will be no more than 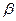 .
.
And how to act if the game is repeated many times? What type of action to choose to increase the minimum guaranteed winnings of player A  and reduce the guaranteed loss of player B
and reduce the guaranteed loss of player B 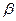 ? In fact, this is the question of the difference section.
? In fact, this is the question of the difference section. 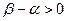 between players A and B with the maximum benefit for each of them. Such a method exists and it consists in a random alternation of pure strategies.
between players A and B with the maximum benefit for each of them. Such a method exists and it consists in a random alternation of pure strategies.
A player's strategy of randomly selecting one of his pure strategies is called a mixed strategy. Thus, a mixed player strategy is a discrete random variable whose values are the numbers of its pure strategies. Denote by P and Q the mixed strategies of players A and B, respectively. Then the mixed strategy P is given by the distribution law:
one | ... | i | ... | m |
p 1 | ... | p i | ... | p m |
where p i 0 is the probability that player A uses the pure strategy A i , and p 1 + p 2 + ... + p i + ... + p m = 1, as the sum of the probabilities of incompatible events (consisting in choosing one of the pure strategies) of the full group. Mixed Q strategy
one | ... | j | ... | n |
q 1 | ... | q j | ... | q n |
where q j 0 is the probability of choice by the player In a pure strategy, q j and q 1 + q 2 + ... + q j + ... + q n = 1.
Pure strategy is obviously a special case mixed for p i or q j = 1.
The average winnings of player A in a game with a mixed strategy are expressed by the mathematical expectation of his winnings.
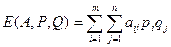
By analogy with games that have a saddle point, a definition is also introduced: the optimal mixed strategies are those sets P; Q that satisfy the equality
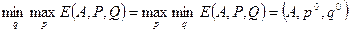
The value of E (A, p 0 , q 0 ) is called the price of the game and is denoted by the letter 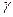 . The price of a mixed game satisfies the condition:
. The price of a mixed game satisfies the condition: 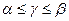
Optimally mixed strategies and the price of a mixed game (P 0 , Q 0 , 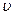 ) are called a matrix game solution.
) are called a matrix game solution.
Von Neumann's theorem (the main theorem of matrix games). Any matrix game has at least one solution in mixed strategies, that is, there is a price for playing in mixed strategies and optimal mixed strategies P 0 and Q 0, respectively, players A and B.
The optimal mixed strategy is the equilibrium of such a game, that is, there is no sense for any player to deviate from it.
Game solution (2  2)
2)
Let the matrix of game 2 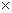 2 does not have a saddle point. Writing down the price of the game and attaching the probability normalization condition to it, we have two systems of equations:
2 does not have a saddle point. Writing down the price of the game and attaching the probability normalization condition to it, we have two systems of equations:
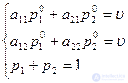
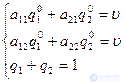
From here, the solution is easily found: 
and the price of the game is defined as:
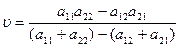
Graphic solution of games.
Consider a 2xn game:
q 1 B 1 | q 2 B 2 | ... | q n B n | |
p 1 , A 1 | a 11 | a 12 | ... | a 1n |
p 2 = 1-p 1 , A 2 | a 21 | a 22 | ... | a 2n |
The game assumes that player A mixes the strategies А 1 and А 2 with probabilities р 1 and р 2 = 1-р 1 . Player B mixes strategies B 1 , B 2 , ..., B n with probabilities q 1 , q 2 , ..., q n , q 1 + q 2 + ... + q n = 1. The expected winnings of player A, corresponding to the j-th pure strategy of player B are
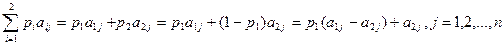
Therefore, Player A is looking for a p 1 value that maximizes the minimum expected wins.
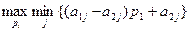
Consider a specific 2x4 game.
B 1 | B 2 | B 3 | B 4 | |
A 1 | 2 | 2 | 3 | -one |
A 2 | four | 3 | 2 | 6 |
There is no saddle point, therefore, the game is solved in mixed strategies. The expected winnings of player A, corresponding to pure strategies of player B, are
Net strategies Player B | Expected winnings Player A |
one 2 3 four | -2 p 1 +4 - p 1 +3 p 1 +2 -7p 1 +6 |
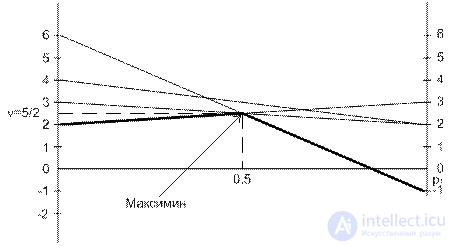
We draw four lines corresponding to pure strategies of player B. To determine the best outcome from the worst, we construct the lower envelope. It represents the worst (minimum) winnings of player A, regardless of the player’s behavior B. To the maximin solution corresponds to the maximum of the lower envelope at the point 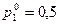 . This point is the intersection of lines 3 and 4. Therefore, the optimal solution for player A is mixing A 1 and A 2 strategies with probabilities of 0.5 and 0.5. The price of the game can be found graphically and can be from the equations of lines 3 and 4:
. This point is the intersection of lines 3 and 4. Therefore, the optimal solution for player A is mixing A 1 and A 2 strategies with probabilities of 0.5 and 0.5. The price of the game can be found graphically and can be from the equations of lines 3 and 4:
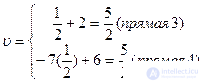
The optimal mixed strategy of player B is determined by two strategies that form the lower envelope. This means that player B can mix strategies B 3 and B 4 , that is, q 1 = q 2 = 0, q 4 = 1-q 3 .
Player B payments expected:
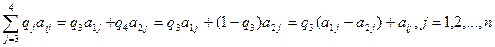
Pure player strategies a | Player B payments expected |
one 2 | 4q 3 -1 -4q 3 +6 |
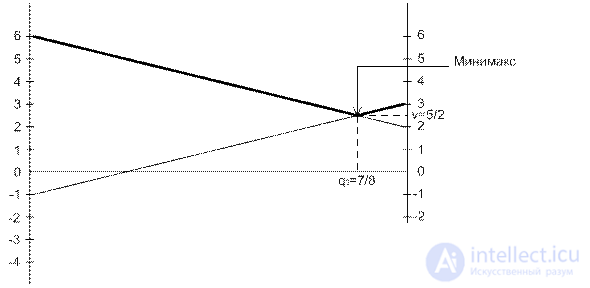 The best worst-case solution for B is the minimum point of the upper envelope.
The best worst-case solution for B is the minimum point of the upper envelope.
4q 3 -1 = -4q 3 +6, q 3 = 7/8
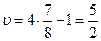
For mx2, the solution is the same. The main difference is that the graphs of functions are constructed here, representing the expected payments of the second player, corresponding to the pure strategies of player A. Then a search is made for the minimax point of the upper envelope.
Matrix game as a linear programming problem.
Consider the matrix game given by the matrix:
AT BUT | one | 2 | ... | j | ... | n |
one | a 11 | a 12 | ... | a 1j | ... | a 1n |
2 | a 21 | a 22 | ... | a 2j | ... | a 2n |
... | ... | ... | ... | ... | ... | ... |
i | a i1 | a i2 | ... | a ij | a in | |
... | ... | ... | ... | ... | ... | ... |
m | a m1 | a m2 | ... | a mj | ... | a mn |
We assume that all elements of the payment matrix are non-negative (if this is not the case, it is possible to add some sufficiently large number L to all elements of the matrix, which translates payments into a region of non-negative values). The price of the game will increase by L, and the solution of the problem will not change. Therefore, we can accept that 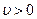 .
.
Let the payment matrix of the game does not contain a saddle point, therefore the game is solved in mixed strategies:
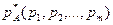

Player A applies the best mixed strategy. 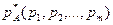 guarantees him, regardless of the behavior of player B, the gain, not less than the price of the game υ.
guarantees him, regardless of the behavior of player B, the gain, not less than the price of the game υ.
.
Comments
To leave a comment
Mathematical methods of research operations. The theory of games and schedules.
Terms: Mathematical methods of research operations. The theory of games and schedules.