7 algorithm of the branch and bound method Tasks that are reduced to integer ones. Tasks about indivisibility. The task of a traveling salesman. The problem of the distribution of investments.

We formulate an algorithm for the branch and bound method. Suppose that the maximization problem is solved. Let us set the lower limit of the optimal value of the objective function z of the CPU problem equal to - 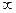Put i = 0.

Step 1. (Probing and determining the boundary.) Select the i-th subtask of linear programming LPi for the study. Solve LPi and probe it, and one of three situations is possible:

a) The optimal value of the objective function of the LPi problem cannot improve the current lower bound.

b) LPi leads to a better valid integer solution than the current lower bound

c) LPi has no valid solutions.

Two options are possible:

a) If the LPi task is probed, the lower bound will change only if the best value of the CPU problem is found. If all subtasks are probed, it is necessary to finish the calculations: the optimal solution to the CPU problem is the one that corresponds to the current lower boundary, if one exists. Otherwise, put i = i + 1 and repeat Step 1.

b) If the LPi task is not probed, proceed to Step 2 to complete branching.

Step 2. (Branching) Select one of the integer variables x _j , the optimal value x _j * in the optimal solution of the LPi problem is not an integer. We exclude from the space of feasible solutions [x _j *] j * <[x _j *] + 1 by forming two LP subtasks that correspond to the constraints x _j 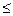[x _j *] and x _j 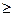[x _j *] + 1 ..

Set i = i + 1 and go to Step 1.

To solve the minimization problem in the algorithm, it is necessary to replace the lower boundary of the upper one (whose initial value is equal to ).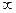

Tasks that are integer.

Tasks about indivisibility.

1. Coverage problems of the set .

An example of a set covering problem is the problem of placing warehouses, in which the distance from the warehouse to each consumer does not exceed 100 km. Another example is the determination of the number and location of student dormitories, in which a student spends no more than 1 hour on the way to the university, the task of placing fire brigades, in which the distance to any point in the city is covered in 5 minutes.

The problem of covering a set can be formulated as follows:

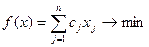
under restrictions:

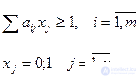
The quantities a _ij are called coverage coefficients. They take values ​​equal to one if the consumer is within the j-th area (covered by the j-th area), and is equal to zero otherwise. Similarly, x _j takes a value equal to one if an object is located in the j-th region and is equal to zero otherwise. Task constraints require that each of m consumers be “covered” with at least one of the n objects. The goal in this case is to “cover” consumers with minimal costs, with c _{j being the} cost of placing an object in the j-th area. Since the task is integer, any method for solving CPU problems can be applied to it.

Example. The University establishes a helpline on the campus. It is advisable to set the minimum number of telephones so that at least one telephone is located on each of the streets of the town.

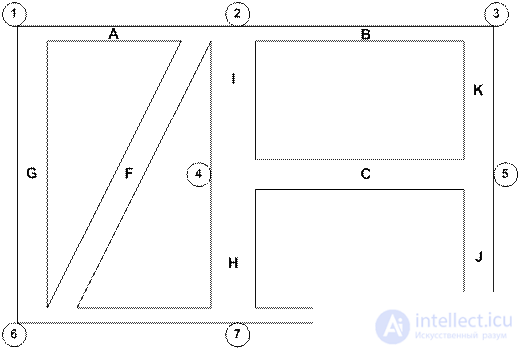
It is logical to arrange the phones at the intersections of the streets so that each telephone can serve at least two streets. The figure shows that this location requires no more than 8 phones.

Let the variable x _j be 1 if the phone is located at j (j = 1..8) and 0 otherwise. The task requires placing at least one telephone on each of the 11 streets (from A to K). Therefore, the task is formed as follows: z = x ₁ + x ₂ + x ₃ + x ₄ + x ₅ + x ₆ + x ₇ + x ₈ 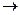min,

x ₁ + x ₂ 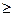1 (A)

x ₂ + x ₃ 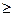1 (B)

x ₄ + x ₅ 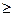1 (C)

x ₇ + x ₈ 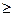1 (D)

x ₆ + x ₇ 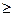1 (E)

x ₂ + x ₆ 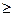1 (F)

x ₁ + x ₆ 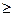1 (G)

x ₄ + x ₇ 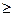1 (H)

x ₂ + x ₄ 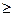1 (i)

x ₅ + x ₈ 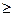1 (J)

x ₃ + x ₅ 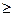1 (K)

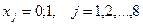
As you can see, all model variables are binary. In this case, aij = 1 for all j. In general, they may be different. The task belongs to the combinatorial class.

The task of a traveling salesman.

In 1831 a book was published in Germany called “Who is a traveling salesman and what should he do for his prosperity?”. One of the recommendations of the book said: “It is important to visit as many places of possible sale as possible, without visiting any of them twice.” Apparently, this was the first formulation of the traveling salesman problem.

There are n cities. The distances between any pair of cities are known and constitute a _ij (i, j = 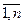, i j). If there is no direct route between cities i and j, aa _ij = . Distances between cities are conveniently written in the form of a matrix A = (a _ij ) _{n n} , where a _ij = .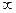

j i	one	2	...	n
one		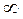a 12	...	a 1n
2	a 21		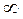...	a 2n
...	...	...	...	...
n	a n1	a n2	...

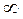In the general case, the matrix is ​​asymmetric.

When traveling from the source city, the traveling agent must visit each of the cities only once and return to the source city. It is necessary to determine the sequence of detour cities so that the length of the route was minimal.

If the task is defined in terms of graph theory, the cities correspond to the vertices of the graph, and the roads correspond to the arcs. The task is to determine the Hamiltonian contour of the minimum length. A Hamiltonian contour is a path that passes through all the vertices of the graph whose initial vertex coincides with the final one. Under the length of the contour understand the sum of the lengths of the arcs.

We define boolean variables as follows:

1, if a traveling salesman moves from city i to city j (i, j = )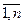

x _ij =

0 otherwise.

Then the task is to describe the variables x _ij :

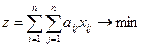(one)

with restrictions:

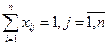(entrance to the city j) (2)

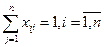(leaving town i) (3)

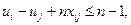(four)

In principle, the variables u _i , i = 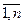can take arbitrary values, but without any damage they can be imposed condition of negativity and integerness.

Conditions a _ij = 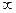in the optimal solution, the values ​​x _ij = 1 are excluded, as having no meaning. Restrictions (2) require that the route include only one entrance to each city, and (3) - only one exit from each city. The objective function (1) is the length of the Hamiltonian contour.

The solution of the problem described only by conditions (1) - (3) is not necessarily a contour passing through all cities. In particular, by solving (1) - (3) two or more disconnected contours can be obtained. To eliminate the possibility of the formation of non-Hamiltonian circuits are limitations (4). We show that they really exclude all partial contours and do not exclude any Hamiltonian contours.

Consider a partial contour passing through the kth city (k ij = 1 for k variables. Adding all inequalities of the form (4) containing k variables x _ij = 1, we obtain the inequality 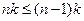which is unacceptable (differences u _i -u _j mutually destroyed). Consequently, (4) excludes the possibility of the formation of any partial contour.

Now we establish that there exist values ​​of the variables u _i that satisfy constraints (4) for any Hamiltonian contour. Suppose that u _i = p (p = 1,2, ... n), if the city i in the Hamiltonian circuit is visited in the order of Pm, and u ₁ = 1 and u _j = u _i +1, j = 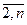; j is the number of the city in the Hamiltonian circuit. So, for example, in the circuit 1-3-6-8- ... the values ​​of u _i will be as follows: u ₁ = 1, u ₃ = 2, u ₆ = 3, u ₈ = 4, ... From this assumption it follows that for x _ij = 0 the corresponding inequality (4) takes the form u _i -u _j n-1 and is always satisfied, since u _i j > 1 with j1. When x _ij = 1, these constraints are satisfied as equalities: u _i + u _j + nx _ij = p- (p + 1) + n = n-1.

Thus it is proved that for any Hamiltonian contour there exist values ​​of the variables u _i that satisfy the constraints (4).

When solving a traveling salesman problem, brute force requires (n-1)! options. Already with the number of cities 16-20, the time to solve the problem increases to astronomical numbers. Therefore, the task of a traveling salesman is solved by ILP methods.

The task of the traveling salesman is reduced to the problem of optimal use of vehicles (milk tanker, tanker).

The problem of the distribution of investments.

Five options are evaluated in terms of the possibility of financing them for the next 3 years. The table contains the expected profit from the implementation of each project and the distribution of investments by years.

It is necessary to determine the set of projects, which corresponds to the maximum total profit. The task is reduced to “yes - no” solutions for each project, that is, binary variables

1 if project j is approved

x _j =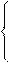

0 if project j is not approved

The CPP’s task is as follows:

z = 20x ₁ + 40x ₂ + 20x ₃ + 15x ₄ + 30x ₅ 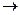max

5x ₁ + 4x ₂ + 3x ₃ + 7x ₄ + 8x 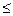₅ 25

x ₁ + 7x ₂ + 9x ₃ + 4x ₄ + 6x 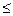₅ 25

8x ₁ + 10x ₂ + 2x ₃ + x ₄ + 10x 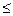₅ 25

x ₁ x ₂ x ₃ x ₄ 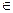{0,1}.