Lecture
The search section presents multi-agent variants of the environment in which each particular agent is forced to take into account the actions of other agents and determine how they will affect its own well-being. The unpredictability of the actions of these other agents may require the agent to take into account many possible unforeseen situations in the process of solving the problem, as was described in the article .
The distinction between cooperative and competitive multi-agent environment options has also been shown in the section. The presence of competitive environment in which the goals of agents conflict, leads to the emergence of search problems in the conditions of opposition, often called games.
In the mathematical theory of games , one of the branches of the economy, any multi-agent variants of the environment are considered as games, provided that the influence of each agent on the others is “significant”, regardless of whether the agents are cooperative or competitive. In artificial intelligence, “games” are usually called rather specific forms of interaction between agents, which are referred to as game theorists as deterministic, alternate, covering two players of zero-sum games with complete information.
In the terminology adopted in this article, this corresponds to deterministic, fully observable variants of the environment in which there are two agents who are obliged to alternate their actions, and in which the utility values at the end of the game are always equal and opposite. For example, if one player wins a chess game (+1), the other player necessarily loses (-1). In such a situation, the conditions for counteraction arise precisely because of this opposition of the utility functions of the agents. In this section of the site, we will briefly consider games with several players, games with a nonzero amount, and stochastic games.
The games made people strain their intellectual abilities (sometimes to a threatening degree) throughout the entire existence of civilization. Due to their abstract nature, games are an attractive object of research in the field of artificial intelligence.
The state of the game can be easily imagined, and the behavior of the agents is usually limited to a small number of actions, the results of which are determined using precise rules. Sports games, such as croquet and ice hockey, have much more complex descriptions, a much larger range of possible actions and rather imprecise rules defining the validity of actions. With the exception of the creation of a robot football player, these sports games do not attract much interest in the artificial intelligence community.
Maintaining games was one of the first tasks considered in the field of artificial intelligence. By 1950, almost immediately after computers became programmable, Conrad Zuse (inventor of the first programmable computer and developer of the first programming language), Claude Shannon (founder of information theory), Norbert Wiener and creator of modern control theory were already interested in chess, and Alan Turing . Since then, the level of the game with the use of computers has steadily increased and achieved that the computers have surpassed people in checkers and the game Othello (Reversi), defeated the champions (but not always) in chess and backgammon, and also became competitive in many others games. The main exception is the game go, in which computers still act at the amateur level.
Games, unlike most of the training tasks that were considered in the article , are interesting because it is very difficult to find a solution in them. For example, chess has an average branch ratio of about 35, and the game often lasts up to 50 moves per player, so the search tree has approximately 35,100 or 10,154 nodes (although the search graph includes only 1040 different nodes ).
Therefore, games, like real life, require the ability to make at least some decisions, even if the calculation of the optimal solution is not feasible. In addition, games are severely punished for inefficiency. While the implementation of the A * search , two times less effective than the other implementation, will simply require twice as much time to get a final solution, a chess program that is half the time less efficiently using the time allotted to it will apparently be defeated at the earliest stages of the game. , even with all other things being equal. Therefore, researchers working in the field of gaming have become authors of many interesting ideas on how to ensure the best possible use of time.
We begin the description of this topic with the definition of the concepts of the optimal course of the game and its search algorithm. Then consider the methods of choosing a good move in a limited time. Clipping allows you to ignore those parts of the search tree that do not affect the final choice, and heuristic evaluation functions allow you to approximately calculate the true usefulness of the state without conducting a full search.
Next, we consider such games that include an element of chance, like backgammon; In addition, a bridge is considered below, which includes elements of incomplete information, since not all cards are visible to each player. Finally, this chapter will describe how the latest gaming programs are gradually overcoming the resistance of people in the fight against these programs and what are the directions of future developments.
As a result of studying this chapter, a student should:
know
• concepts of games based on the principle of dominance, Nash equilibrium, what is reverse induction, etc. conceptual approaches to solving the game, the meaning of the concept of rationality and equilibrium within the framework of an interaction strategy;
be able to
• distinguish between games in strategic and expanded forms, build a "game tree"; formulate game models of competition for various types of markets;
own
• methods for determining the outcome of the game.
The first attempt to create a mathematical theory of games was made in 1921 by E. Borel. As an independent field of science, the theory of games was first systematically described in the monograph by G. von Neumann and O. Morgenstern “Game Theory and Economic Behavior” in 1944. Since then, many sections of economic theory (for example, the theory of imperfect competition, the theory of economic stimulation, etc. .) developed in close contact with game theory [1] . Game theory is also successfully applied in the social sciences (for example, the analysis of voting procedures, the search for equilibrium concepts that define cooperative and non-cooperative behavior of individuals). As a rule, voters reject candidates representing extreme points of view, but when one of the two candidates is proposed, offering various compromise solutions, a struggle arises. Even Rousseau’s idea of evolution from “natural freedom” to “civil freedom” formally corresponds from the standpoint of game theory to the point of view of cooperation.
The game is an idealized mathematical model of the collective behavior of several individuals (players), whose interests are different, which causes conflict. The conflict does not necessarily imply the presence of antagonistic contradictions between the parties, but is always associated with a certain kind of disagreement. A conflict situation will be antagonistic if an increase in the gain of one of the parties by a certain amount leads to a decrease in the gain of the other side by the same amount and vice versa. Antagonism of interests gives rise to conflict, and coincidence of interests reduces the game to coordination of actions (cooperation).
Examples of conflict situations are situations that arise in the relationship of the buyer and seller; in the conditions of competition of various firms; in the course of hostilities, etc. Examples of games include ordinary games: chess, checkers, cards, salons, etc. (hence the name "game theory" and its terminology).
In most games arising from the analysis of financial, economic and managerial situations, the interests of the players (parties) are not strictly antagonistic or absolutely identical. The buyer and seller agree that it is in their common interest to agree on a sale, but they are vigorously trading when choosing a specific price within the limits of mutual profitability.
Game theory is a mathematical theory of conflict situations.
The goal of game theory is to develop recommendations for the reasonable behavior of the parties to the conflict (determining optimal strategies for the behavior of players).
A game differs from a real conflict in that it is conducted according to certain rules. These rules establish the sequence of moves, the amount of information on each side of the behavior of the other and the outcome of the game, depending on the situation. The rules also establish the end of the game, when a certain sequence of moves has already been made, and more moves are not allowed.
Game theory, like any mathematical model, has its limitations. One of them is the assumption of the full (ideal) rationality of opponents. In a real conflict, often the optimal strategy is to guess what the adversary is stupid and use this stupidity to their advantage [2] .
Another drawback of game theory is that each of the players should be aware of all possible actions (strategies) of the enemy, only the exact one of which he will use in this game is unknown. In a real conflict, this is usually not the case: the list of all possible strategies of the enemy is just unknown, and the best solution in a conflict situation is often going beyond the strategies known to the enemy, “dumbfounding” him with something completely new, unforeseen.
Game theory does not include elements of risk that inevitably accompany intelligent decisions in real conflicts. It determines the most cautious, reinsurance behavior of the parties to the conflict.
In addition, in game theory, optimal strategies are found for one indicator (criterion). In practical situations, it is often necessary to take into account not one, but several numerical criteria. A strategy that is optimal for one indicator may not be optimal for others.
Aware of these limitations and therefore not blindly adhering to the recommendations of the given game theories, it is still possible to develop a completely acceptable strategy for many real conflict situations.
Currently, research is underway to expand the scope of game theory.
The following definitions of the elements that make up a game are found in the literature.
Players are subjects involved in interactions that are presented in the form of a game. In our case, these are households, firms, government. However, in the case of uncertainty in external circumstances, it is convenient enough to present the random components of the game, independent of the behavior of the players, as actions of "nature".
Rules of the game. By game rules are meant sets of actions or moves available to players. In this case, the actions can be very diverse: decisions of customers about the volumes of purchased goods or services; firms - on production volumes; government tax rate.
Determining the outcome (result) of the game. For each combination of player actions, the outcome of the game is set almost mechanically. The result may be: the composition of the consumer basket, the vector of the company's releases, or a set of other quantitative indicators.
Wins. The meaning of the concept of winning may vary for different types of games. In this case, it is necessary to clearly distinguish between winnings measured on an ordinal scale (for example, utility level), and values for which interval comparison (for example, profit, welfare level makes sense).
Information and expectations. Uncertainty and the constant change of information can extremely seriously influence possible outcomes of interaction. That is why it is necessary to take into account the role of information in the development of the game. In this regard, the concept of the player’s informational set comes to the fore, i.e. the totality of all information about the state of the game that he possesses at key points in time.
When considering players' access to information, an intuitive idea of general knowledge, or common knowledge, is very useful , meaning the following: a fact is well known if all players are aware of it and all players know that other players also know about it.
For cases in which the application of the concept of general knowledge is not enough, the concept of individual expectations of participants is introduced - ideas about how the game situation is at this stage.
Game theory assumes that a game consists of moves performed by players simultaneously or sequentially.
The moves are personal and random. A move is called personal if the player consciously selects it from the set of possible options for actions and implements it (for example, any move in a chess game). A move is called random if its choice is made not by the player, but by some random selection mechanism (for example, according to the results of a coin toss).
The set of moves taken by players from the beginning to the end of the game is called a game.
One of the basic concepts of game theory is the concept of strategy. A player’s strategy is a set of rules that determine the choice of a course of action for each personal move, depending on the situation in the game. In simple (one-way) games, when in each game a player can make only one move, the concepts of strategy and a possible course of action coincide. In this case, the totality of the player’s strategies covers all his possible actions, and any action possible for player i is his strategy. In complex (multi-way games), the concepts of “option of possible actions” and “strategy” may differ from each other.
A player’s strategy is called optimal if it provides the given player with repeated repetition of the game the highest possible average win or the lowest possible average loss, regardless of which strategies the opponent applies. Other optimality criteria may be used.
It is possible that the strategy that provides the maximum gain does not have another important idea of optimality, as the stability (equilibrium) of the solution. The decision of the game is stable (equilibrium) if the strategies corresponding to this decision form a situation that no player is interested in changing.
We repeat that the task of game theory is to find optimal strategies.
The classification of games is presented in Fig. 8.1.
Non-cooperative are games in which players do not have the right to enter into agreements, form coalitions, and the goal of each player is to obtain the greatest possible individual winnings.
Games in which the actions of players are aimed at maximizing the winnings of collectives (coalitions) without their subsequent separation between the players are called coalition.
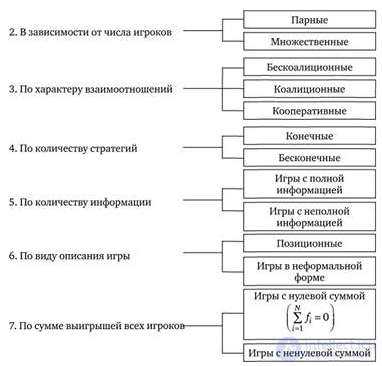
Fig. 8.1. Game classification
The outcome of a cooperative game is the division of the coalition’s win, which arises not as a result of certain actions of players, but as a result of their predetermined agreements.
In accordance with this, in cooperative games, not situations are compared according to preference, as is the case in non-cooperative games, but divisions; and this comparison is not limited to the consideration of individual wins, but is more complex.
There are also reflective games that consider situations with the mental reproduction of a possible course of action and behavior of the enemy.
7. If any possible party of some game has a zero sum of wins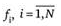 
all N players ( 
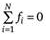), then they talk about a zero-sum game. Otherwise, the games are called nonzero sum games.
Obviously, the pair game with a zero sum is antagonistic, since the gain of one player is equal to the loss of the second, and therefore the goals of these players are directly opposite.
The ultimate zero sum pair game is called matrix game. Such a game is described by a payment matrix in which the winnings of the first player are set. The row number of the matrix corresponds to the number of the applied strategy of the first player, the column to the number of the applied strategy of the second player; at the intersection of the row and column is the corresponding gain of the first player (loss of the second player).
The final pair game with a nonzero sum is called a bimatrix game. Such a game is described by two payment matrices, each for the respective player.
We give the following example. The game "Standings". Let player 1 be the student preparing for the test, and player 2 the teacher taking the test. We assume that the student has two strategies: A1 - prepare well for the test; A 2 - do not prepare. The teacher also has two strategies: B1 - to set off; B 2 - do not set off. For example, the following considerations, reflected in the matrixes of winnings, can be used as the basis for estimating the winnings of players:
This game in accordance with the above classification is strategic, paired, non-cooperative, finite, described in normal form, with a non-zero sum. More briefly, this game can be called bimatrix.
The task is to determine the optimal strategies for the student and for the teacher.
Another example of the well-known bimatrix game Prisoner's Dilemma.
Each of the two players has two strategies: A 2 and B 2 - aggressive behavior strategies, a A i and B i - peaceful behavior. Suppose that “peace” (both players are peaceful) is better for both players than “war”. The case when one player is aggressive and the other peaceful is more profitable for the aggressor. Let the payoff matrices of players 1 and 2 in this bimatrix game have the form
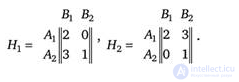
For both players, the aggressive strategies A2 and B2 dominate the peaceful strategies Ax and B v. Thus, the only balance in the dominant strategies is (A2, B2 ), i.e. it is postulated that the result of non-cooperative behavior is war. At the same time, the outcome (A1, B1) (world) gives a greater win for both players. Thus, non-cooperative egoistic behavior conflicts with collective interests. Collective interests dictate the choice of peace strategies. At the same time, if players do not exchange information, war is the most likely outcome.
In this case, the situation (A1, B1) is Pareto optimal. However, this situation is unstable, which leads to the possibility of violation by the players of the established agreement. Indeed, if the first player violates the agreement and the second does not violate, then the gain of the first player will increase to three, and the second will drop to zero and vice versa. Moreover, each player who does not violate the agreement loses more when the second player violates the agreement than in the case when they both violate the agreement.
There are two main forms of the game. The game in extensive form is represented as a diagram of the decision tree type, with the root corresponding to the start point of the game, and the beginning of each new branch called the node, the state reached at this stage with these actions already taken by the players. Each end node - each end point of the game - is associated with a payoff vector, one component for each player.
The strategic, otherwise called normal, form of presentation of the game corresponds to a multidimensional matrix, with each dimension (in the two-dimensional case, rows and columns) includes a set of possible actions for one agent.
A separate matrix cell contains a payoff vector corresponding to this combination of player strategies.
In fig. 8.2 presents an extensive form of the game, and in table. 8.1 - strategic form.
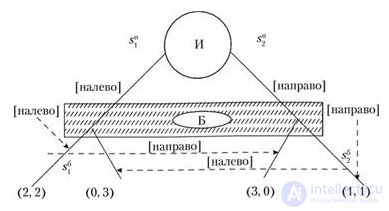
Fig. 8.2. Extensive decision-making game
Table 8.1. Strategic decision-making game
|
Game form |
Sf [left] |
Sf [right] |
|
Sf [left] |
2.2 |
0.3 |
|
Sf [right] |
3.0 |
1,1 |
There is a fairly detailed classification of the components of game theory. One of the most common criteria for such a classification is the division of game theory into the theory of non-cooperative games, in which individuals are the decision-makers, and the theory of cooperative games in which the decision-makers are groups, or coalitions of individuals.
Non-cooperative games are usually presented in normal (strategic) and expanded (extensive) forms.
Comments
To leave a comment
Mathematical methods of research operations. The theory of games and schedules.
Terms: Mathematical methods of research operations. The theory of games and schedules.