Lecture
Integer programming.
The general formulation of the integer programming problem differs from the general LP problem only by the presence of an additional constraint. This limitation is the requirement of integerness : the values of all or part of the variables of the model in the optimal solution are nonnegative integer numbers, that is, they belong to the set N 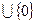 . If this requirement applies to all variables, then the CPU task is called a fully integer task . If it refers only to a part of variables, the task is called partially integer. The LP task, which differs from the CPU task, only the absence of integer requirements, call the task with weakened restrictions corresponding to the given CPU task.
. If this requirement applies to all variables, then the CPU task is called a fully integer task . If it refers only to a part of variables, the task is called partially integer. The LP task, which differs from the CPU task, only the absence of integer requirements, call the task with weakened restrictions corresponding to the given CPU task.
Methods for solving LP problems.
At first glance, the natural method for solving the CPU problem is the rounding method , the implementation of which consists of two stages. At the first stage, the optimal solution of the LP problem with weakened constraints is found. In the second stage, the values of the variables in the optimal solution X * , which are not integers, are rounded so as to obtain a valid solution X ** with integer values.
Is such a method consistent?
Example. Consider a completely integer problem:
x 1 + 1,5x 2 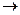 max
max
2x 1 + 4x 2 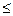 17, 10x 1 + 4x 2
17, 10x 1 + 4x 2 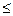 45
45
x 1 x 2 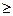 0, x 1, x 2
0, x 1, x 2 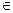 N
N 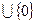 .
.
A constrained LP problem is obtained by removing constraints.
x 1 x 2 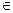 N
N  . Its optimal solution can be obtained graphically.
. Its optimal solution can be obtained graphically.
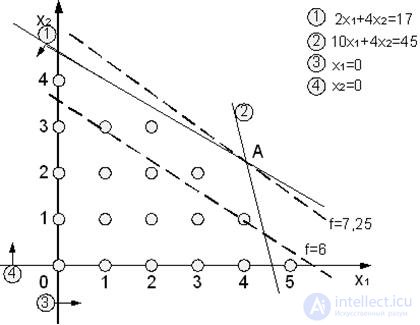
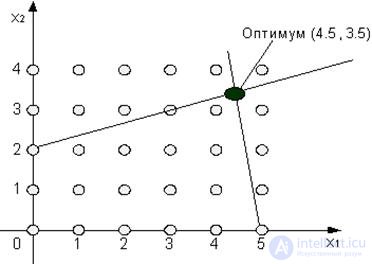
The optimal solution is achieved at point A. The objective function is equal to f = 7.25. The optimal solution is X * = (7/2, 5/2) T. According to the rounding method, we take X ** = (3, 2) T. The value of the objective function in this case is 6. However, in fact, the optimal solution is X o = (2, 3) T , and f opt = 6.5.
So, the rounding method gives a non-optimal solution. Therefore, it is not consistent as a general method for solving CPU problems. In addition, many IO tasks can be formulated as CPU problems, in which model variables take values from the set  .
.
Consider a method known as the clipping method.
Consider an integer problem.
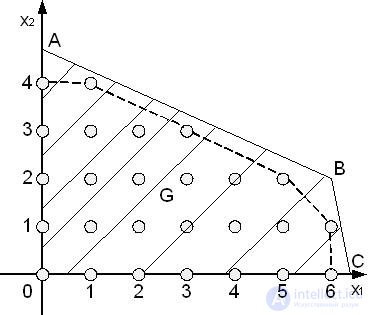
Not all points of the set of admissible solutions G correspond to valid solutions of this problem, but only those that satisfy the requirements of integerness. Theoretically, from the set G one can always distinguish the set G * such that:
a) it contains all points of the set G satisfying the requirement of integerness;
b) it is a convex set;
c) the coordinates of all its extreme points satisfy the requirements of integerness.
If the set G of admissible solutions is replaced by the set G *, this cannot lead to a change in the optimal solution, since G * is obtained from G by cutting off from it a subset that obviously does not contain admissible solutions that satisfy the requirement of integerness. But in this case, the optimal solution of the LP problem with weakened constraints and the set G * of feasible solutions corresponds to the extreme point of the set G *. As a result, it satisfies the requirement of integrity and provides extreme value not only on G *, but also on G.
The basis of combinatorial methods for solving CPU problems is the idea of sorting all the elements of the set G of feasible solutions that satisfy the requirement of integerness.
The most well-known combinatorial method is the branch and bound method . It starts with solving the LP problem with weakened constraints. If the optimal solution X * (point B) does not satisfy the requirement of integer, then from the set G there are two intersecting convex subsets of K 1 and K 2 containing all valid solutions from G that satisfy the requirement of integer, but not containing X *. By this, the CPU task is replaced by a set of two equivalent (in the sense of the optimal solution X o G) problems with sets of feasible solutions K 1 and K 2 , since X o 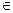 K 1 or X o
K 1 or X o 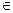 K 2 .
K 2 .
Developed many methods for solving CPU problems. Almost all of these methods can be described on the basis of a single concept consisting of three elements.
Element 1. A procedure is envisaged for forming and solving a sequence of interrelated tasks, which are called tasks generated by the original task or tasks - origins . At the same time, the optimal solution for at least one of the tasks - the sources must coincide with the optimal solution of the problem that generated them.
Element 2. Each problem generated by the original problem is associated with the so-called weakened problem (a problem with weakened restrictions). Its optimal solution can be found at a much lower cost than the optimal solution of the corresponding source task.
Element 3 . As a result of the analysis of the solution of a weakened problem, a decision is made that relates to the task - the source:
a) exclude it from consideration;
b) replace with one generated task selected by a certain rule;
c) replace the system generated tasks.
The method of cutting planes (Gomory method).
The method was developed by R. Gomori in 1957-1958. MOS refers to the cut-off methods and is called the correct cut-off method.
An example . Let it be necessary to find a solution to a completely integer problem:
2x 1 + x 2 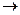 max
max
0.75x 1 + 1.5x 2 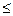 4.8 (1)
4.8 (1)
x 1 x 2 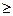 0, x 1, x 2
0, x 1, x 2 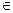 N
N 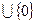 .
.
Let there be some LP task:
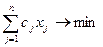
with restrictions:
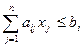 i =
i = 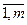 (2)
(2)
x j 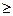 0, j =
0, j = 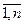 (3)
(3)
with integer restrictions:
x j 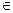 N
N 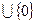 j =
j = 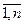 (four)
(four)
The integer part of a is the largest integer [a], not exceeding a. The fractional part of a is the number {a} = a - [a].
Gomory's method is as follows. Let the weakened problem (1) - (3) be solved and the system obtained at the last iteration:
x 1 + α 1 m +1 x m +1 +… + α 1 n x n = β 1 ,
x 2 + α 2 m +1 x m +1 +… + α 2 n x n = β 2 , (5)
. . . . . . . . . . . . . .
x m + α nm +1 x m +1 + ... + α mn x n = β m
those. there is a solution to the problem
(β 1 , ..., β m , 0, ..., 0) (6)
Suppose that this solution does not satisfy the integer condition (4), i.e. some β i , i = 1, ..., m, non-integer.
Add to system (6), which is equivalent to system (2), the constraint:
{β i } - 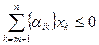 (7)
(7)
Line i is called generating. This restriction cuts off the optimal point (β 1 , ..., β m , 0, ..., 0) from the original polyhedron of solutions, without affecting any of the integer points of the set.
We show that a valid integer solution satisfies relation (7). From system (5) we have:
x i + 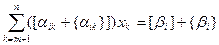 or x i +
or x i + 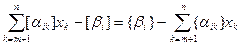
Let x = (x 1 , ..., x n ) be an integer feasible solution. Then the left side of the last expression is integer, i.e. integer is the value:
{β i } - 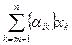
Then, if relation (7) were not satisfied, i.e. would be performed:
{β i } - 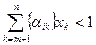 ,
,
then due to the fact that 0 {β i } <1, 0 {α ik } <1, x k 0, the following relation would have to hold:
{β i } -, 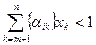
and this contradicts the integer {β i } - 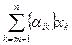 .
.
Now check the clipping condition. Because for the optimal solution {β i }> 0, x i = 0, i = m + 1, ..., n, i.e. this solution really does not satisfy (7).
So, if to (6) or to (2) - which is equivalent - to add the constraint (7) and solve the problem (1) - (3) and (7), then we get a solution that is different from (β 1 , ..., β m , 0, ..., 0), which may also be non-integer. This will require the addition of new constraints of the form (7). If each time the index i in constraints (7) is chosen so that it is the index in the first order of a variable with a non-integer value, the admissible set of problem (1) - (3) is bounded and not empty, then the Gomori algorithm is finite, that is . ends in a finite number of steps by solving an integer problem.
Despite the fact that the Gomory method is a reliable solution for CPU problems, its practical application is impractical if the original problem has a higher dimension.
Illustration of the Gomory Method.
Z = 7x 1 + 10x 2 ,
-x 1 + 3x 2 6,
7x 1 + x 2 35,
x 1 x 2 0 x 1 x 2 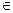 N
N 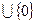 .
.
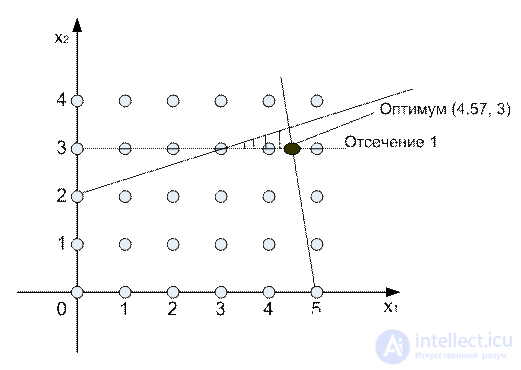

Clipping does not discard any source of permissible integer point, but must pass through at least one integer point (valid or invalid).
The method of branches and boundaries.
It was first offered by Land and Deutsch in the 1960s. then improved Little, Murthy, Souni, Carol.
Consider the following LP integer problem:
z = 5x 1 + 4x 2  max
max
x 1 + x 2  five
five
10x 1 + 6x 2 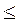 45
45
x 1 x 2 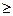 0,
0, 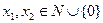
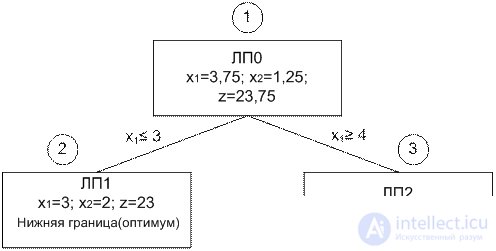
The corresponding weakened LP problem has a solution: x 1 = 3.75, x 2 = 1.25, z = 23.75
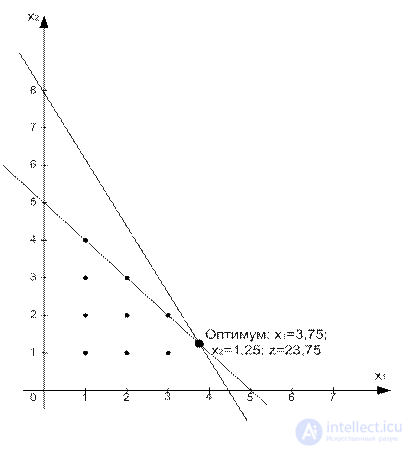
The optimal solution of the LP0 problem (we denote it this way) does not satisfy the condition of integerness.
The branch and bound method changes the solution space of the LP problem so that ultimately the optimal solution of the CPU problem is formed. To do this, first select one of the integer variables, the value of which in the optimal solution LP0 is not integer. For example, choosing x 1 (= 3.75), we note that the region 3 1 <4 of the space of feasible solutions of the LP0 problem does not contain integer values x 1 , and therefore it can be excluded from consideration as unpromising. This is equivalent to replacing the original LP0 task with two new LP1 and LP2 tasks:
The space of feasible solutions LP1 = The space of feasible solutions LP0 + (x 1  3)
3)
The space of feasible solutions LP2 = The space of feasible solutions LP0 + (x 1  four).
four).
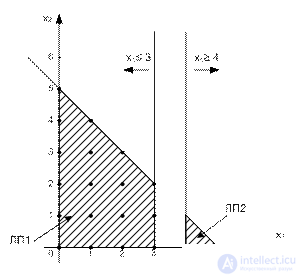
All admissible solutions of the CPU problem remained, tasks LP1 and LP2 "will not lose" any solution.
New restrictions (x 1  3) and (x 1
3) and (x 1 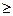 4) are mutually exclusive, so the tasks LP1 and LP2 should be considered as independent. Dichotomization of LP tasks is the basis of the concept of branching in the branch and bound method. In this case, x 1 is called a branch variable.
4) are mutually exclusive, so the tasks LP1 and LP2 should be considered as independent. Dichotomization of LP tasks is the basis of the concept of branching in the branch and bound method. In this case, x 1 is called a branch variable.
The optimal solution is either in the EOD of the problem LP1, or the task LP2. Therefore both tasks must be solved.
We solve LP1:
z = 5x 1 + 4x 2 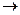 max
max
x 1 + x 2 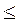 five
five
10x 1 + 6x 2 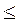 45
45
x 1 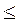 3
3
x 1 x 2 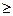 0
0
Solution: x 1 = 3, x 2 = 2, z = 23.
The optimal solution of the LP1 problem satisfies the condition of the integer variables x 1 and x 2 . In this case, they say that task LP1 is probed. This means that the LP1 task should no longer be probed, it cannot contain a better solution to the CPU problem than it already is.
For now, we can say that z = 23 is the lower bound.
Now we go to the problem LP2. Since the optimal value of z = 23.75 and all its coefficients are integers in the LP0 problem, it is impossible to obtain an integer solution in the LP2 problem. The task LP2 is rejected and we consider it probed.
The implementation of the branch and bound method is complete. The optimal solution: x 1 = 3, x 2 = 2, z = 23.
Two questions remained unanswered:
1) Was it possible to select the variable x 2 as the branch variable instead of x 1 in the LP0 task?
2) Was it possible to first solve the problem LP2 instead of LP1?
Both answers are positive, but the further course of the decision may differ. If we solve the problem LP2, we get the following scheme:
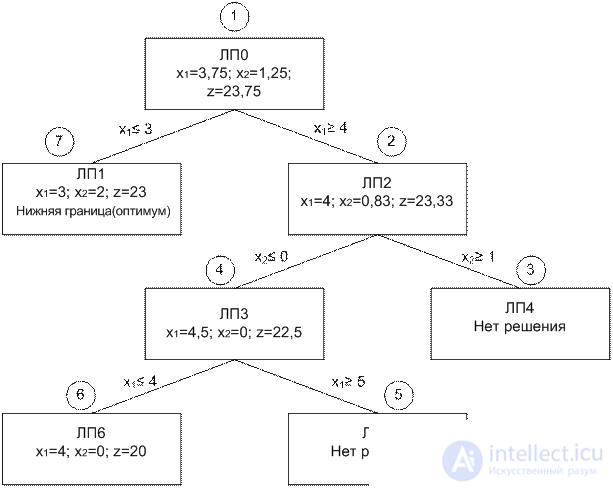
The sequence of subtasks is the worst. The example points out the main weakness of the branch and bound method: how to choose a branch variable and how to choose the next subtask? There is no strict theory about this.
Comments
To leave a comment
Mathematical methods of research operations. The theory of games and schedules.
Terms: Mathematical methods of research operations. The theory of games and schedules.