11 Methods of game theory in operations research. Matrix games. Lower and upper bound of the game. Minimax principle

Methods of game theory in operations research.

In solving the tasks of the Oncological Institute, it is necessary to analyze situations in which at least two sides encounter different goals and interests. The result of the event of each of the parties in such a situation depends on what type of action the opposite party chooses. Such situations are called conflict situations. Conflict does not necessarily imply antagonistic contradictions of the parties, but always involves disagreements.

The conflict situation is characterized by the following features:

1) the presence of several stakeholders (consumers, companies of the country, individuals, military units)

2) the existence of possible actions of each of the parties

3) presence of interests of the parties (increase in revenues, ousting competitors from the market, etc.)

A mathematical model of a conflict situation is called a game. The section of operations research dealing with mathematical models of making optimal decisions in the conditions of conflict is called game theory. A game is a mathematical model of a real conflict situation, the analysis of which is carried out according to certain rules.

Interested parties of the game (in particular, individuals) are called players. Games vary in the number of players. It is said that there is a game of N persons if the players break up into N disjoint sets in such a way that the players in each set have the same interests. This game is called plural. If N = 2, then the game is called a pair. In a multiple game, participants may form coalitions (permanent or temporary). A multiple game with two standing coalitions is a steam room. Further we consider only pair games.

In order to subject the game to mathematical analysis, the rules of the game must be formed, that is, the system regulating:

- possible options for players;

- the amount of information each side about the behavior of the other;

- the result (outcome) of the game, to which each given set of moves leads.

This result (gain or loss) does not always have a quantitative expression, but usually it is possible, at least conditionally, to express it by number (chess).

A game is called a zero-sum game if the sum of the winnings of all players is zero (that is, each player wins at the expense of others). A zero-sum pair game is called a game with a strict rivalry or antagonistic one. Examples of non-zero-sum games are lotteries, sweepstakes, card games with a "banker".

Suppose there is a pair game with zero sum U in which two players A and B participate. Usually, for convenience, side A is called “we”, and side B is called “enemy”.

The development of the game over time is a series of sequential actions or moves. A move is a choice of one of the actions provided by the rules and its implementation. Moves are personal and random. A personal move is a player’s conscious choice of one of the options and its implementation. A random move is a choice made not by the decision of the player, but by any random selection mechanism (draw). Some games consist only of random moves, they are called gambling and are not considered in game theory. Some games consist only of personal moves (checkers, chess). Most card games contain both types of moves. Game Theory analyzes games with personal moves.

A player's strategy is a set of rules that determine the choice of options for each personal move of this player, depending on the situation during the game.

A game is called finite, if each player has only a finite number of strategies, otherwise the game is called infinite.

The optimal strategy of the player is called such a strategy, which, with repeated repetition of the game provides the player with the highest possible average gain (or, equivalently, the minimum average loss). The choice of the optimal strategy is based on the principle of equal rationality, assuming that both players are equally reasonable and the behavior of each is aimed at preventing the opponent from achieving his goal.

Thus, game theory does not take into account the mistakes and miscalculations of the players, as well as the elements of excitement and risk.

Matrix games.

Consider the ultimate antagonistic pair game. Player A has m strategies, and Player B has n strategies. This game is called the game m * n. A set of strategies (A i , B j ) uniquely determines the outcome of the game under the assumption that the game is played in pure strategies.

If each player chooses a strategy unambiguously with probability 1, then they say that he uses a pure strategy. Suppose that we know the values ​​(A i , B j ) for each pair of strategies. These values ​​can be written in the form of a matrix, the rows of which correspond to the strategies of player A i , and the columns to the strategies of player B j .

B j A i	B 1	B 2	...	B n
A 1	a 11	a 12	...	a 1n
A 2	a 21	a 22	...	a 2n
...	...	...	...	...	...
A m	a m1	a m2	...	a mn
			...

Column maxima

This matrix is ​​called the payment matrix, the winning matrix, or the game matrix.

The lower and upper bound of the game. The minimax principle.

We consider only pure strategies. The decision of the game is to determine the best strategy for each player.

Find min a ij = 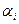(minimum lines). Choosing strategy А i , player A should count on the fact that as a result of the actions of the enemy he will win only 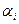. Naturally, acting most cautiously (that is, avoiding any risk), you need to choose the strategy for which 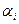maximum, that is:

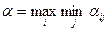
Magnitude 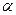is called the lower price of the game, otherwise the maximum win or maximin.

The lower price of the game is a guaranteed winnings of player A with any strategy of player B. This is a guaranteed minimum that A can secure himself by adhering to the most cautious strategy. Player A strategy corresponding to the maximum 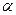called maximin strategy. This is a strategy based on the basic principle of game theory - the principle of caution is based on the minimax principle: it is necessary to act in such a way that with the worst behavior of the adversary to get the maximum gain.

If you select for each column 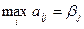and find 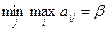we will get the top price of the game 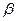- guaranteed loss of player B in any strategy of player A. 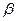- Also called minimax or minimax loss. The corresponding strategy is called minimax.

The principle of caution, which dictates to players the choice of appropriate strategies (maximin and minimax) is fundamental in game theory and is called the minimax principle.

It can be shown that the inequality is always valid for the lower and upper prices of the game:

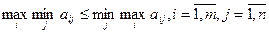
or

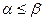
There are games for which the lower price is equal to the upper one, i.e. 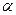= 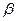. . Such games are called saddle point games.

The total value of the lower and upper price of the game in games with a saddle point is called the pure saddle point, and the i * and j * strategies that allow to achieve this value are the optimal pure strategies. A pair of optimal pure strategies (i *, j *) is called the saddle point of the matrix, since the element a i * j * = 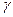is both minimum in the i-th row and maximum in the j-th column. Optimal strategies and the net price of the game are its solution. The game itself is said to be solved in pure strategies.

The criterion for the existence of the price of a game in pure strategies is the following theorem:

In order for the price of the game to exist in pure strategies, that is, to ensure that the lower price of the game 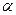equaled the top price of the game, 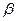it is necessary and sufficient existence of a saddle point for this game.

The saddle point of the game (matrix A) is a pair of numbers (i *, j *) such that a i * j * is at the same time the maximum of its row and the minimum of its column.

For a game with a saddle point, there is a property of equilibrium (or stability): each player is not interested in moving away from the optimal strategy, since his gain will decrease.

A sign of the presence of a saddle point and an equilibrium pair of strategies is the equality of the upper and lower price of the game. The presence of a saddle point in the game is far from the rule, but rather the exception. But there are games that always have a saddle point. These are the so-called games with complete information. A game with complete information is a game in which each player knows the results of all previous moves, both personal and random, for each personal move. (checkers, chess, tic-tac-toe)

It can be proved that every game with complete information has a saddle point and is solved in pure strategies.