Probability element

In real life, there are many unpredictable external events, due to which people end up in unforeseen situations. This unpredictability is reflected in many games by incorporating an element of chance, such as throwing lots. Thus, games with elements of randomness allow us to come one step closer to reality, and therefore it makes sense to consider how this affects the decision-making process.

One of the typical games that combine luck and art, are backgammon. Before each turn, a player rolls dice to determine permissible moves. For example, in the backgammon position shown in the figure, White dropped 6–5 points and they have four possible moves.

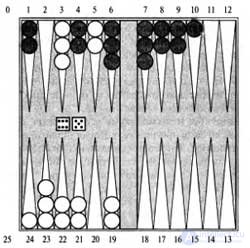
The typical position of the game of backgammon. The goal of the game is to remove all the pieces from the board. White moves clockwise to field 25, and black - counterclockwise to field 0. A chip can move to any field if there are not several opponent's chips on it; if there is only one opponent piece on this field, it is captured and must start its movement from the very beginning. In the position shown here, White, after throwing lots, received points 6-5 and must choose among four permissible moves: (5-10,5-11), (5-11,19-24), (5-10,10-16) and (5-11,11-16)

Although White knows what their permissible moves are, they do not know which points will be brought by drawing lots for black, and therefore they cannot determine what Black’s permissible moves will be. This means that whites do not have the opportunity to form a standard game tree of the type that we encountered in chess, as well as tic-tac-toe. The backgammon tree, except for the MAX and MIN nodes, must include the draw lots. Knots of the drawing are marked with circles in the picture.

The branches leading from each node of the draw indicate the possible results of the toss-up of a lot, therefore each of them is marked with an inscription indicating the number of points and the probability with which these points can be obtained. There are 36 different combinations of points on two dice, and they are all equally probable; but since combinations of points such as 6-5 and 5-6 are the same, there are only 21 distinct combinations of points. The probability of the appearance of six doubles (from 1-1 to 6-6) is 1/36, and each of the 15 other different combinations of points has a probability of 1/18.

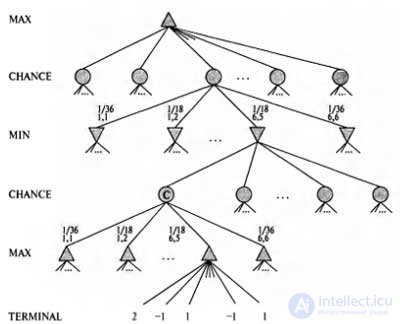Schematic representation of the game tree for one of the backgammon positions

The next step is to understand how to make the right decisions. Of course, in this case it is required to find a move that leads to the best position. However, the resulting positions do not have certain minimax values. Instead, it is possible to calculate only the expected value, in which the expected result is set taking into account all possible loss of the lot that may occur. This leads to a generalization of the minimax value for deterministic games to the expected minimax value (expectiminimax value) for games with draw lots.

Terminal nodes and max and MIN nodes (for which the results of the draw are known) are used in the same way as before, and the draw blocks are evaluated by obtaining a weighted average of the values ​​obtained as a result of all possible depositions of lots, i.e. in the following way:

where the function of determining the successor of the to-do n node simply complements the state n with each possible loss of a draw to form each successor s, and P (s) is the probability with which the draw occurs. The results of the calculation of these equations can be reserved recursively in all nodes up to the root of the tree in the same way as in the minimax algorithm. We leave the reader to work out all the details of this algorithm as an exercise.