Some applications of operational calculus

1. Solution of the Cauchy problem for a linear differential equation with constant coefficients

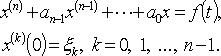
Applying the Laplace transform and using the theorem on the differentiation of the original, we arrive at the equation

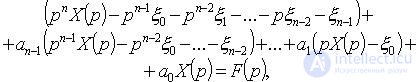
Where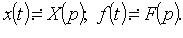

Transforming, we obtain the equation of the form 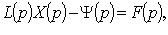from where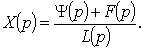

From the last relation, we get the opportunity to find the original x (t) from its image X (p) .

Initial task 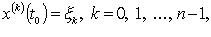reduced by replacing 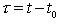to described.

2. Solution of the Cauchy problem for systems of linear differential equations with constant coefficients. The scheme of application of the Laplace transform is the same as in paragraph 1.

Example.

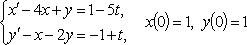
Applying the Laplace transform, we arrive at an algebraic system:

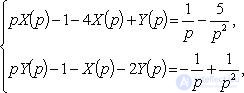
from where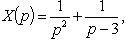

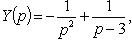
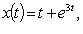
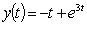
3. Solution of Voltaire integral equations of convolution type

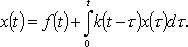
Applying the Laplace transform, we obtain

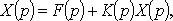
Where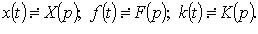

From the last equation, we express X (p) and, by X (p), we find the original x (t) —the solution of the integral equation.

4. Calculation of improper integrals.

If f = F , g = G , then

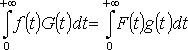
(Parseval formula).