The complex analysis ^[1] , the theory of the complex variable (or the complex variable ; abbreviated DFT ), is a section of mathematical analysis that examines and studies the functions of a complex argument.

General concepts

Each complex function 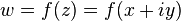can be considered as a pair of real functions of two variables: 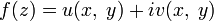, determining its real and imaginary part, respectively. Functions 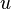, 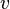are called components of a complex function .

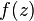Further everywhere, where it is said about the boundedness of a complex function, we mean the boundedness of its module (which implies boundedness in the usual sense of both components).

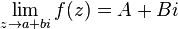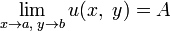The concept of a limit for a sequence and a function is introduced in the same way as in the real case, with the absolute value replaced by a complex module. If a then and 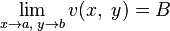. The reverse is also true: the existence of the limits of the components implies the existence of the limit of the function itself, and the components of the limit are the limits of the components. The continuity of a complex function is also defined in the same way as in the real case, and it is equivalent to the continuity of both its components.

All the main theorems on the limit and continuity of real functions also take place in the complex case, if this extension is not related to the comparison of the complex values ​​by more or less . For example, there is no direct analogue of the theorem on intermediate values ​​of a continuous function.

- neighborhood of number 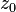defined as a set of points 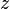remote from 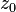less than :

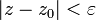
On the complex plane -the neighborhood is the interior of a circle of radius centered on .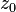

Infinitely distant point

In complex analysis, it is often useful to consider the full complex plane ^[2] , supplemented in comparison with the usual infinite point : 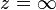. With this approach, an unboundedly increasing (modulo) sequence is assumed to converge to an infinitely distant point. Algebraic operations with infinity are not performed, although several algebraic relations take place:

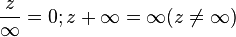
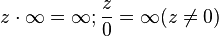
a neighborhood of an infinity point is considered to be a set of points. 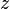whose module is greater than that is, the outer part - surroundings origin.

Differentiation

Definition

Derivative for a complex function of one argument 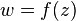is defined in the same way as for real:

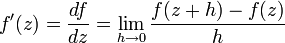
(here - complex number). If this limit exists, the function is called differentiable or holomorphic . Wherein

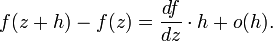
One important feature should be taken into account: since the complex function is defined on the plane, the existence of the given limit means that it is the same when it tends to from any direction. This fact imposes significant restrictions on the type of component functions. 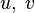and determines their rigid relationship (Cauchy – Riemann conditions):

It follows that the differentiability of the components 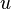and 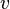not enough for the differentiability of the function itself.

Moreover, the following properties distinguish the complex analysis from the real one:

• Any differentiable in some neighborhood of a point A complex function is differentiable an unlimited number of times and is analytic, that is, its Taylor series converges to a given function at all points in this neighborhood (along with the term analytic function , its synonym “holomorphic function” is also used).
• (Liouville theorem): If a function is differentiable on the whole complex plane and is not a constant, then its module cannot be bounded.
• Both components of a differentiated complex function are harmonic functions, that is, they satisfy the Laplace equation:

• Any harmonic function can be either a real or imaginary component of a differentiable function. In this case, the other component is determined uniquely (from the Cauchy – Riemann conditions), up to a constant term.

Thus, any differentiable complex function is a function of the form 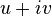where 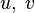- interrelated harmonic functions of two arguments.

Other properties

Let functions 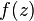and 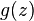differentiable in the field 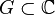. Then 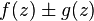and 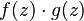also differentiable in this area. If a 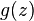in the area of 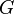not drawn to zero then 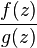will be differentiable in 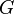. Composition of functions 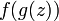differentiable wherever it is defined. If the derivative of the function 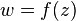in the area of 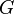does not vanish, then there is a function inverse to it 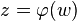and it will be differentiable.

The derivative for the sum, difference, product, quotient of division, composition of functions and inverse function is calculated by the same formulas as in real analysis.

Geometrical meaning of the derivative

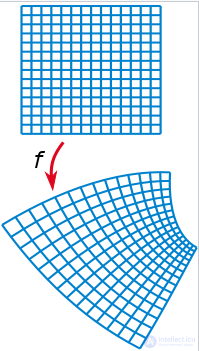
An example of a conformal mapping. It is seen that the corners are saved.

Each complex function 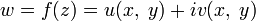defines a mapping of the complex plane with coordinates 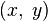to another complex plane with coordinates 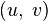. The expression:

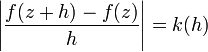
with little 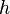geometrically can be interpreted as a scaling factor that performs this mapping when moving from a point 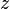to the point 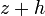. Existence limit 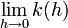that is, the derivative module 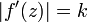, means that the scaling factor is the same in any direction from the point 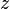, that is, does not depend on direction. Generally speaking, the scaling factor varies from point to point.

If the scaling factor 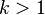then around the point 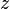the distances between the points increase, and the scaling factor is called the stretch factor . If the scaling factor 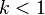then around the point 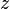the distances between points decrease, and the scaling factor is called the compression ratio .

As for the derivative argument, it determines the angle of rotation of a smooth curve passing through the point 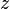. All smooth curves under this map are rotated by the same angle. Mappings that preserve angles are called conformal; thus, any differentiable complex function defines a conformal mapping (in the domain where its derivative does not vanish). This fact is associated with the wide application of complex functions in cartography and hydrodynamics ^[3] .

Integration

The concept of a primitive complex function (an indefinite integral) is introduced in the same way as in the real case. However, the analogue of a certain integral in the interval from 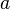before 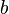on the complex plane, generally speaking, does not exist, since the path from the starting point to the final one is ambiguous. Therefore, the main type of complex integral is a curvilinear integral depending on a particular path. Below are the conditions under which the integral does not depend on the path, and then the integral “from point to point” can be defined correctly.

Let the equation defines some piecewise smooth curve 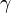in the complex plane, and the function 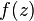defined at points of this curve. We divide the parameter setting interval by 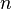equal parts: 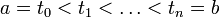and consider the integral sum:

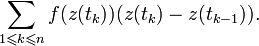
The limit of this amount with an unlimited increase 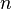is called a (complex) integral over a curve 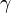from this function 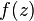; it is designated:

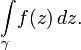
For any function 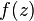continuous along 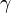, this integral exists and can be calculated through the usual real integral over the parameter:

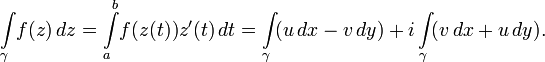
Here 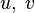- Components 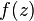. It immediately follows from this representation that the properties of the complex integral are similar to the properties of a real curvilinear integral.

Contour integral

Of particular practical interest are integrals over a (closed) contour, that is, along a piecewise smooth curve without self-intersection points, for which the starting point coincides with the end point. The contour can be bypassed in two directions; Positive is the direction in which the region bounded by the contour is on the left in the direction of travel.

If the curve forms a closed loop, uses the special designation of the integral:

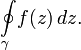
There is an important integral Cauchy theorem: for any function 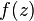, analytic in a simply connected domain 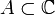and for any closed loop 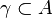Fairly correlation:

.

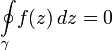Corollary: let the function 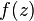, analytic in a simply connected domain 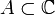and dots 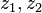from the area 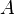connected by some curve 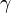. Then the integral 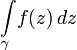depends only on points 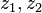but not on the choice of the connecting curve 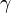so you can label it 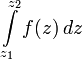and the Newton – Leibniz theorem holds:

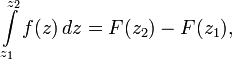
where F (z) is antiderivative for .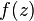

Other powerful tools for the study of complex and real integrals:

• Cauchy integral formula and its corollaries: maximum modulus principle, mean theorems
• The main theorem on deductions

Uniqueness theorems and analytic continuation

Zero function 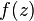called point 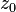in which the function vanishes: .

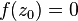Theorem on the zeros of an analytic function . If the zeros of the function 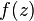analytical in the field 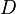, have a limit point inside 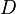then function 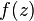everywhere in 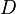equals zero.

Corollary: if the function 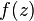analytical in the field 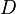and is not identically zero, then in any bounded closed subregion 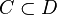it can only have a finite number of zeros.

Uniqueness theorem for an analytic function . Let be 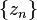- converging sequence of different points of the area 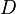. If two analytic functions 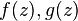coincide at all points of this sequence, they are identically equal in .

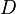In particular, if two analytic functions coincide on some piecewise smooth curve in 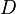then they match everywhere in 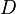. This means that the values ​​of the analytic function, even in a small area of ​​the domain, completely determine the behavior of the function in the entire domain of its definition. By specifying an analytic function on a curve (for example, on the real axis), we uniquely determine its extension (if it is possible) to a wider area, which is called the analytic continuation of the original function.

All standard analysis functions — polynomial, fractional-linear function, power function, exponent, trigonometric functions, inverse trigonometric functions, logarithm — allow analytic continuation to the complex plane. Moreover, for their analytic continuations, the same algebraic, differential and other identities will take place as for the real original, for example:

Decomposition

Power series

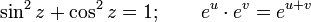
Determining the sum of a numerical series and signs of convergence in complex analysis are almost the same as in the real one, with the absolute value replaced with a complex module; The exception is the signs of convergence in which the comparison is made for more or less elements of the series themselves, and not for their modules.

Any differentiable at a point 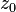the function decomposes in a neighborhood of this point in a Taylor power series:

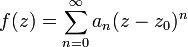
The coefficients of the series are calculated by the usual formulas. This series converges to the function 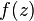in some circle of radius 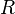centered on 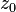which serves as an analogue of the convergence interval of a real series. In this circle, the series is absolutely converging, and outside it diverges. In this case, there are 3 cases.

1. The series converges in a circle of finite and nonzero radius.
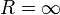2. The series converges in the entire complex plane, that is, . Such functions are called integers .
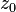3. The series only converges at a point. . Example: 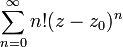. Such points 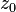are called special for function 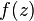. Non-singular points are called correct . The interior of the circle of convergence consists of regular points.

The boundary of the circle of convergence contains at least one singular point. It follows that the radius of the circle of convergence at 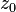equals distance from 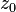to the nearest point to it.

Abel's theorem : if 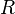- the radius of the circle of convergence of the power series, then in any circle with the same center, but smaller radius, the series converges uniformly.

Laurent Series

It is of great practical interest to study the behavior of a function near an isolated singular point, that is, a point in the vicinity of which the function is analytic, but at the point itself is either not analytic or not defined. The power series is useless here, so a more general Laurent series is introduced:

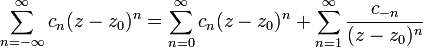
If the region of convergence of the Laurent series is not empty, it is a circular ring: .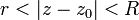

The main theorem : if the function analytic in a circular ring, then it can be represented in this ring by the convergent Laurent series, and uniquely.

As for the power series, the boundaries of the convergence ring are determined by the distribution of the singular points of the function. By the appearance of the Laurent series, some conclusions can be drawn about the behavior of the function near the point .

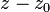1. Removable singular point: if the Laurent series does not contain elements with negative powers . Then it’s just a power series defining a function in some circle surrounding 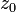.The sum of the series in this circle is finite and can differ from 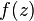only at a point 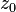, so it is enough to override it in order for the function to become analytic in the whole circle. The following sign takes place: if the function near is 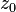analytic and bounded, then 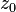is a removable singular point.
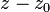2. Pole: if the Laurent series contains a finite number of elements with negative powers .In this case, the function at the point is 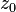infinite (modulo).
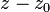3. Существенно особая точка: если ряд Лорана содержит бесконечное число элементов с отрицательными степенями . В этом случае функция в точке 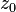не может быть корректно определена так, чтобы быть непрерывной.

Приложения в вещественном анализе

С помощью теории вычетов, являющейся частью ТФКП, вычисляются многие сложные интегралы по замкнутым контурам.

Средствами комплексного анализа объясняются некоторые моменты, не поддающиеся простой интерпретации в терминах вещественного анализа. Приведем классический пример: функция

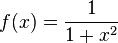
непрерывна и бесконечно дифференцируема на всей вещественной прямой. Рассмотрим её ряд Тейлора

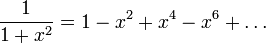
Этот ряд сходится только в интервале 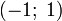, хотя точки 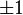не являются какими-то особенными для .

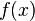Положение проясняется при переходе к функции комплексного переменного 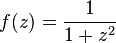, у которой обнаруживаются две особые точки: 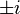. Соответственно, эту функцию можно разложить в ряд Тейлора только в круге .

History

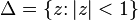Fundamental work in complex analysis is associated with the names of Euler, Riemann, Cauchy, Weierstrass and many other famous mathematicians. The theory of conformal mappings began to develop rapidly due to the existing applications in engineering, and methods and results of complex analysis are also used in analytical number theory. A new surge of interest in complex analysis is associated with complex dynamics and the theory of fractals.

see also

• Analytical function
• Deduction (complex analysis)
• Holomorphic function
• Quaternion Analysis
• Complex numbers
• Multivariate complex analysis
• Monogenic function