Deduction (complex analysis)

In complex analysis, the deduction of a given object (function, form) is an object (number, form, or cohomological class of a form) that characterizes the local properties of a given one.

History [edit]

The theory of residues of a complex variable was mainly developed by O. Cauchy in 1825–1829. Besides him, important and interesting results were obtained by S. Hermite, J. Sohotsky, E. Lindelöf and many others.

In 1887, A. Poincaré generalized the Cauchy integral theorem and the notion of residue to the case of two variables ^[1] , from this moment the multidimensional theory of residues originates. However, it turned out that this concept can be generalized in various ways.

Designation [edit]

To denote the analytical function deduction 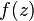at the point 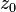expression is applied 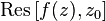from English Residue . In some literature it is designated as 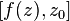^[2] .

One-dimensional complex analysis [edit]

Definition [edit]

Let be 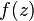- complex-valued function in the region 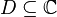holomorphic in some punctured neighborhood of a point .

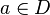Deduction function 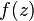at the point 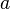called number

.

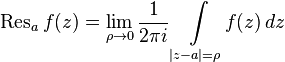Since the function is holomorphic in a small punctured neighborhood of a point 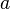according to the Cauchy theorem, the value of the integral does not depend on 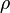for sufficiently small values ​​of this parameter, as well as on the form of the path of integration. It is only important that the path is a closed curve in the domain of the analyticity of the function, which once covers the point in question and no other points belonging to the domain of holomorphy. .

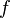In some neighborhood of a point 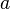function 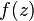seems to converge near laurent by degrees 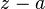. It is easy to show that the deduction coincides with the coefficient of the series 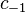at 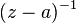. Often this representation is taken as the definition of the function deduction.

Deduction in "infinity" [edit]

To enable a more complete study of the properties of a function, the concept of residue at infinity is introduced, and it is considered as a function on the Riemann sphere. Let the infinitely remote point be an isolated singular point. 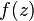, then a deduction at infinity is called a complex number, equal to

.

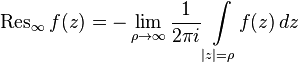The integration cycle in this definition is oriented positively, that is, counterclockwise.

Similar to the previous case, the residue at infinity has a representation in the form of the coefficient of the Laurent decomposition in the neighborhood of the infinitely distant point :

.

Differential form deduction [edit]

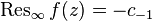From the point of view of analysis on manifolds, to introduce a special definition for some selected point of the Riemann sphere (in this case, infinitely remote) is unnatural. Moreover, such an approach is difficult to generalize to higher dimensions. Therefore, the concept of deduction is introduced not for functions, but for differential -forms on the Riemann sphere:

.

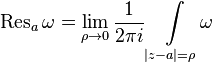At first glance, there is no difference in definitions, but now 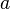- arbitrary point 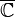, and the change of sign in the calculation of the deduction at infinity is achieved by changing the variables in the integral.

Logarithmic deductions [edit]

Integral 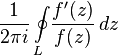called the logarithmic function residue 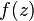relative to the contour .

The notion of a logarithmic residue is used to prove the theorem of Rushe and the main theorem of algebra

Ways to calculate deductions [edit]

According to the definition, a deduction can be calculated as a contour integral, but in the general case it is rather laborious. Therefore, in practice, they mainly use the consequences of the definition:

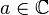• In a removable singular point , as well as at the point of regularity, the deduction of the function 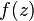equals zero. At the same time, this statement is not true for an infinitely remote point. For example, the function 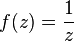has a first-order zero at infinity, however 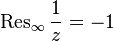. The reason for this is that the form 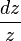has a peculiarity both at zero and at infinity.

• At the pole multiplicities deduction can be calculated by the formula: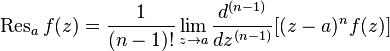

,

special case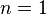

.

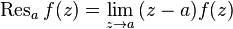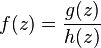• If the function has a simple pole at a point 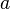where 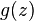and 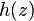holomorphic in the neighborhood 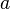functions, 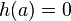, , 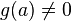then you can use a simpler formula:

.

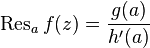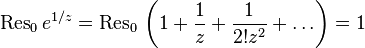• Very often, especially in the case of essentially singular points, it is convenient to calculate the residue using the decomposition of a function in a Laurent series. For example, , as the coefficient at 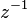equals 1.

Deduction Theory Applications [edit]

In most cases, the theory of residues is used to calculate various kinds of integral expressions using the main theorem on residues. Often useful in these cases is the Lemma of Jordan.

Calculations of certain integrals of trigonometric functions [edit]

Let function 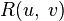- rational function of variables 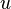and 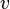. To calculate the integrals of the form 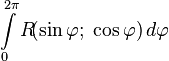It is convenient to use Euler formulas. Putting that 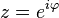, and making the appropriate transformations, we get:

.

Calculation of improper integrals [edit]

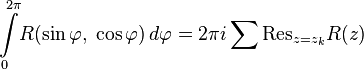To calculate improper integrals using the theory of residues use the following two lemmas:

1. Let the function 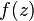holomorphic in the upper half-plane 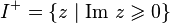and on the real axis except for a finite number 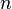poles not lying on the real axis and 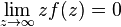. Then

.

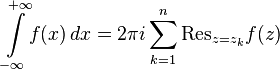2. Let the function 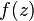holomorphic in the upper half-plane 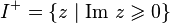and on the real axis except for a finite number 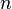poles not lying on the real axis 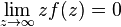and 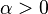. Then

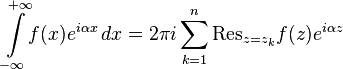
Moreover, the integrals in the left-hand sides of equalities are not obliged to exist and, therefore, are understood only in the sense of the principal value (Cauchy formula).

Multidimensional Complex Analysis [edit]

Form-deduction and class-deduction [edit]

This section is not complete. You will help the project by correcting and adding it.

Local Deduction [edit]

This section is not complete. You will help the project by correcting and adding it.

The deductible flow [edit]

This section is not complete. You will help the project by correcting and adding it.