Lecture
Antiholomorphic functions (also called antianalytic functions ) are a family of functions that are closely related to holomorphic functions.
Function 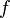 defined on an open subset
defined on an open subset 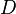 complex plane is called antiholomorphic if its derivative
complex plane is called antiholomorphic if its derivative 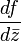 by
by 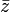 exists at all points of this set. This is equivalent to the condition
exists at all points of this set. This is equivalent to the condition
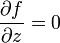
which can be given a view similar to Cauchy - Riemann conditions:
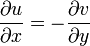
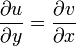
Where
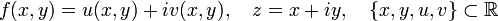
A function that depends simultaneously on 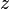 and
and 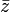 , is neither holomorphic nor antiholomorphic.
, is neither holomorphic nor antiholomorphic.
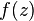 holomorphic in
holomorphic in 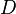 then and only if
then and only if 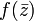 antiholomorphic in
antiholomorphic in 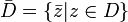 .
. 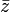 in the neighborhood of each point of its domain.
in the neighborhood of each point of its domain. 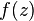 holomorphic in
holomorphic in 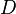 then and only if
then and only if 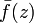 antiholomorphic in
antiholomorphic in 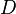 .
.
Comments
To leave a comment
Comprehensive analysis and operational calculus
Terms: Comprehensive analysis and operational calculus