Comprehensive function

The term complex function can refer to two types of functions:

Complex function [edit]

The complex-valued function is a function of a real variable having complex values:

.

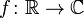Such a function can be represented as

,

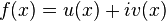Where 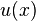and 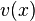- real functions. Function 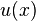called the real part of the function 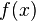, but 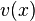- its imaginary part .

Complex Variable Function [edit]

This concept is a generalization of the previous version:

.

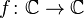Such functions are handled by a separate area of ​​mathematical analysis - the theory of functions of a complex variable, or complex analysis.

The function can also be represented as

,

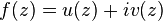however, there is a deeper connection between 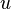and 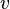. For example, in order to function 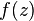was differentiable, the Cauchy – Riemann conditions must be satisfied:

;

.

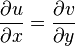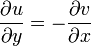Examples of analytic functions of a complex variable are: a power function, an exponent, a gamma function, a Riemann zeta function and many others, as well as their inverse functions and any combinations thereof. However, the real part of the complex number 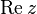, complex part 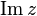complex conjugation 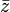module 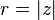and argument 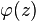analytical functions of a complex variable are not, since they do not satisfy the Cauchy – Riemann conditions.