This term has other meanings, see Gamma.
Gamma function is a mathematical function that extends the concept of factorial to the field of complex numbers. Usually denoted by 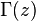 .
.
It was introduced by Leonard Euler, and the gamma function is due to Legendre.
Content
- 1 Definitions
- 1.1 Integral definition
- 1.2 Definition by Gauss
- 1.3 Definition by Euler
- 1.4 Definition by Weierstrass
- 1.5 Notes
- 2 Related definitions
- 3 Properties
- 4 Literature
- 5 See also
Definitions [edit]
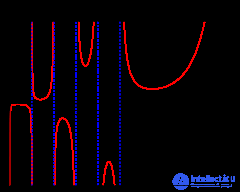
Graph of the gamma function of a real variable
Integral definition [edit]
If the real part of the complex number 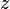 is positive, then the gamma function is determined through the integral
is positive, then the gamma function is determined through the integral
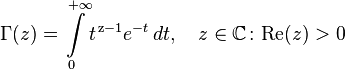
Throughout the entire complex plane, the function extends analytically through the identity
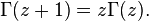
There is a direct analytic continuation of the initial formula to the whole complex plane, called the Riemann – Hankel integral
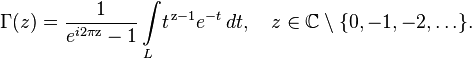
where is the contour 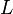 - any contour on the complex plane, bypassing the point
- any contour on the complex plane, bypassing the point 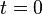 counterclockwise, and the ends of which go to infinity along the positive real axis.
counterclockwise, and the ends of which go to infinity along the positive real axis.
Subsequent expressions are alternative definitions of the gamma function.
Gauss definition [edit]
It is true for all complex 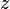 , with the exception of 0 and negative integers
, with the exception of 0 and negative integers
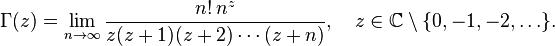
Euler Definition [edit]
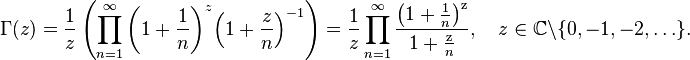
Weierstrass Definition [edit]
Where 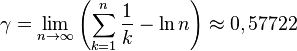 - Euler's constant - Mascheroni.
- Euler's constant - Mascheroni.
Remarks [edit]
- The integral above converges absolutely if the real part of the complex number
 is positive.
is positive. - Applying integration by parts, it can be shown that the identity
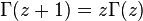
- executed for the integrand.
- And since
 for all positive integers
for all positive integers 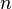
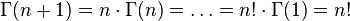
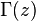 is meromorphic on the complex plane and having poles at the points
is meromorphic on the complex plane and having poles at the points 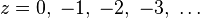
Related definitions [edit]
- Sometimes an alternative entry is used, the so-called pi function , which depends on the gamma function as follows:
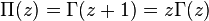 .
.
- In the integral above, which defines the gamma function, the limits of integration are fixed. Consider also the incomplete gamma function defined by a similar integral with variable upper or lower integration limit. Distinguish the upper incomplete gamma function, often denoted as a gamma function from two arguments:
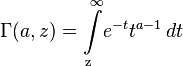
and the lower incomplete gamma function, similarly denoted by the lowercase letter "gamma":
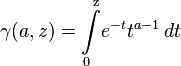 .
.
Properties [edit]
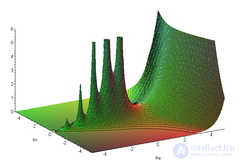
Graph module gamma functions on the complex plane.
- Euler's Supplement Formula :
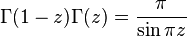 .
.
- From it follows the Gauss multiplication formula en ru :
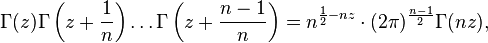
- which for n = 2 is called the Legendre doubling formula:
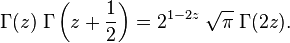
- The best-known values of the gamma function from a non-integer argument are
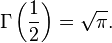
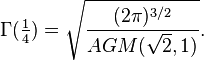
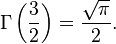
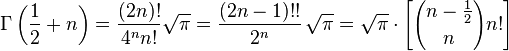
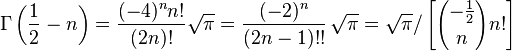
- Gamma function has a pole in
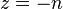 for any natural
for any natural 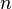 and zero; the deduction at this point is set as follows
and zero; the deduction at this point is set as follows 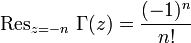 .
.
- The following infinite product for the gamma function, as Weierstrass showed, is true for all complex
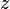 non-positive integers:
non-positive integers: 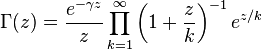 ,
,
- Where
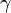 - this is Euler's constant.
- this is Euler's constant.
- The main, but useful property that can be obtained from the limit definition:
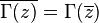 .
.
- The gamma function is differentiable an infinite number of times, and
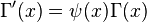 where
where 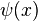 often referred to as the “psi function,” or digamma function.
often referred to as the “psi function,” or digamma function. - The gamma function and beta function are related as follows:
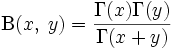 .
.
Literature [edit]
Kuznetsov D.S. Special functions (1962) - 249 p.
See also [edit]
- List of objects named after Leonard Euler
- K-function
- Barnes G-function
- Beta function
- Gamma distribution
- Incomplete gamma function
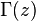 .
. 
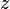 is positive, then the gamma function is determined through the integral
is positive, then the gamma function is determined through the integral 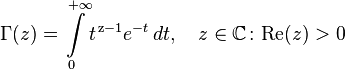
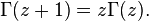
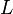 - any contour on the complex plane, bypassing the point
- any contour on the complex plane, bypassing the point 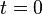 counterclockwise, and the ends of which go to infinity along the positive real axis.
counterclockwise, and the ends of which go to infinity along the positive real axis. 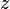 , with the exception of 0 and negative integers
, with the exception of 0 and negative integers 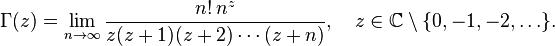
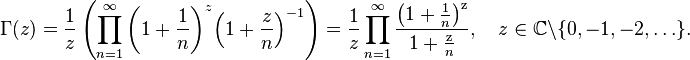
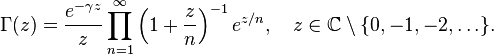
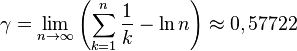 - Euler's constant - Mascheroni.
- Euler's constant - Mascheroni. 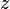 is positive.
is positive. 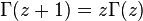
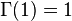 for all positive integers
for all positive integers 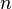
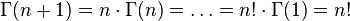
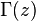 is meromorphic on the complex plane and having poles at the points
is meromorphic on the complex plane and having poles at the points 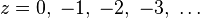
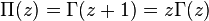 .
. 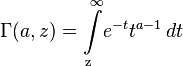
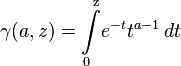 .
. 
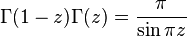 .
. 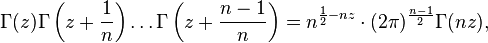
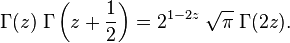
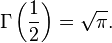
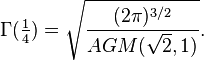
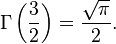
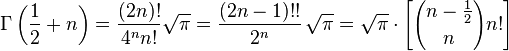
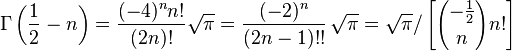
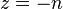 for any natural
for any natural 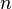 and zero; the deduction at this point is set as follows
and zero; the deduction at this point is set as follows 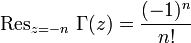 .
. 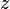 non-positive integers:
non-positive integers:  ,
,  - this is Euler's constant.
- this is Euler's constant.  .
.  where
where 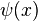 often referred to as the “psi function,” or digamma function.
often referred to as the “psi function,” or digamma function. 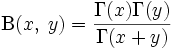 .
.
Comments
To leave a comment
Comprehensive analysis and operational calculus
Terms: Comprehensive analysis and operational calculus