Lecture
Complex logarithm is an analytic function obtained by extending the real logarithm to the entire complex plane (except for zero). There are several equivalent ways to do this. This feature is widely used in complex analysis. In contrast to the real case, the complex logarithm function is multivalued.
For complex numbers, the logarithm can be defined in the same way as for real numbers, that is, as the inversion of an indicative function. In practice, only the natural complex logarithm is used, the base of which is the Euler number  : it is usually indicated
: it is usually indicated 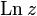 .
.
The natural logarithm of a complex number |
Other equivalent definitions are given below.
In the field of complex numbers, the solution of this equation, in contrast to the real case, is not uniquely determined. For example, according to Euler's identity, 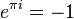 ; however also
; however also 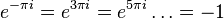 . This is due to the fact that the exponential function along the imaginary axis is periodic (with a period
. This is due to the fact that the exponential function along the imaginary axis is periodic (with a period 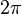 ) [2] , and the same value of the function takes infinitely many times. Thus, the complex logarithmic function
) [2] , and the same value of the function takes infinitely many times. Thus, the complex logarithmic function 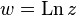 is multi-valued.
is multi-valued.
Complex zero has no logarithm, since complex exponent does not take a zero value. Non-zero 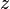 can be presented in indicative form:
can be presented in indicative form:
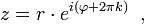 Where
Where 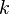 - arbitrary integer
- arbitrary integer Then 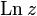 is the formula [3] :
is the formula [3] :
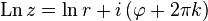
Here 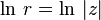 - real logarithm. From here follows:
- real logarithm. From here follows:
Complex logarithm |
It can be seen from the formula that for one and only one of the values the imaginary part is in the interval 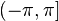 . This value is called the main value of the complex natural logarithm [1] . The corresponding (already unambiguous) function is called the main branch of the logarithm and is denoted by
. This value is called the main value of the complex natural logarithm [1] . The corresponding (already unambiguous) function is called the main branch of the logarithm and is denoted by 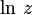 . Sometimes through
. Sometimes through 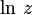 also denote the logarithm value, not lying on the main branch. If a
also denote the logarithm value, not lying on the main branch. If a 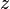 - a real number, then the principal value of its logarithm coincides with the usual real logarithm.
- a real number, then the principal value of its logarithm coincides with the usual real logarithm.
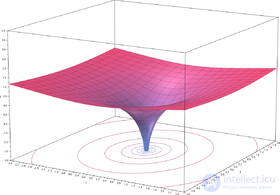
It also follows from the above formula that the real part of the logarithm is defined as follows through the components of the argument:
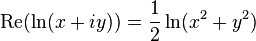
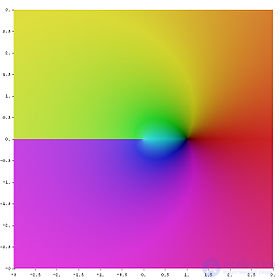
The figure shows that the real part as a function of the components is centrally symmetric and depends only on the distance to the origin of coordinates. It is obtained by rotating the graph of the real logarithm around the vertical axis. As it approaches zero, the function tends to 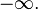
The logarithm of a negative number is found by the formula [3] :

We give the main value of the logarithm (  ) and its general expression (
) and its general expression ( 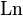 ) for some arguments:
) for some arguments:
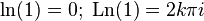
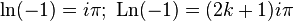
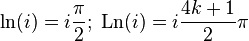
You should be careful when converting complex logarithms, taking into account that they are multi-valued, and therefore equality of these expressions does not follow from the equality of the logarithms of any expressions. Example of erroneous reasoning:
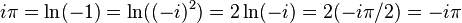 - a clear mistake.
- a clear mistake. Note that the main logarithm value is on the left, and the value from the underlying branch is on the right ( 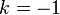 ). The cause of the error is careless use of the property
). The cause of the error is careless use of the property 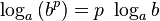 which, generally speaking, in the complex case implies the entire infinite set of logarithm values, and not just the main value.
which, generally speaking, in the complex case implies the entire infinite set of logarithm values, and not just the main value.
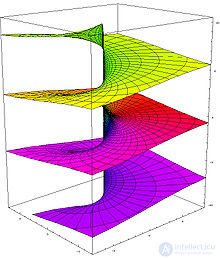
In complex analysis, instead of considering multivalued functions on a complex plane, a different decision was made: to consider a function as single-valued, but not defined on a plane, but on a more complex manifold, which is called a Riemann surface [4] . The complex logarithmic function also falls into this category: its image (see figure) consists of an infinite number of branches twisted in the form of a spiral. This surface is continuous and simply connected. The only zero of the function (first order) is obtained by 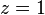 . Special points:
. Special points: 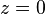 and
and  (branch points of infinite order) [5] .
(branch points of infinite order) [5] .
By virtue of the simply connectedness, the Riemann surface of the logarithm is a universal covering [6] for a complex plane without a point 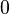 .
.
The logarithm of a complex number can also be defined as the analytic continuation of the real logarithm to the entire complex plane. Let the curve  starts at one, does not pass through zero and does not cross the negative part of the real axis. Then the principal value of the logarithm at the end point
starts at one, does not pass through zero and does not cross the negative part of the real axis. Then the principal value of the logarithm at the end point 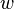 crooked
crooked 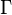 can be determined by the formula [5] :
can be determined by the formula [5] :
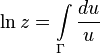
If a 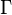 - a simple curve (without self-intersections), then for numbers lying on it, logarithmic identities can be applied without fear, for example:
- a simple curve (without self-intersections), then for numbers lying on it, logarithmic identities can be applied without fear, for example:
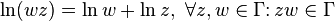
The main branch of the logarithmic function is continuous and differentiable on the whole complex plane, except for the negative part of the real axis, on which the imaginary part abruptly changes to 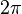 . But this fact is a consequence of the artificial limitation of the imaginary part of the main value by the interval
. But this fact is a consequence of the artificial limitation of the imaginary part of the main value by the interval 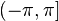 . If we consider all branches of a function, then continuity takes place at all points except zero, where the function is not defined. If you allow the curve
. If we consider all branches of a function, then continuity takes place at all points except zero, where the function is not defined. If you allow the curve 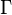 intersect the negative part of the real axis, the first such intersection transfers the result from the branch of the principal value to the neighboring branch, and each subsequent intersection causes a similar displacement along the branches of the logarithmic function [5] (see figure).
intersect the negative part of the real axis, the first such intersection transfers the result from the branch of the principal value to the neighboring branch, and each subsequent intersection causes a similar displacement along the branches of the logarithmic function [5] (see figure).
It follows from the analytic continuation formula that on any branch of the logarithm [2] :
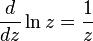
For any circle 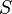 covering the point
covering the point 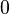 :
:
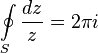
The integral is taken in the positive direction (counterclockwise). This identity underlies the theory of residues.
You can also define the analytic continuation of the complex logarithm using series known for the real case:
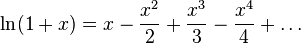 | (Row 1) |
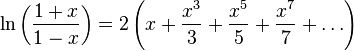 | (Row 2) |
However, from the form of these series it follows that in the unit the sum of the series is zero, that is, the series refers only to the main branch of the multivalued function of the complex logarithm. The radius of convergence of both series is 1.
Since complex trigonometric functions are associated with the exponent (Euler formula), the complex logarithm as an inverse of the exponential function is associated with companion trigonometric functions [7] [8] :
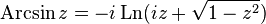
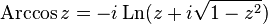
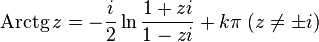
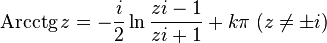
Hyperbolic functions on the complex plane can be considered as trigonometric functions of an imaginary argument, so there is a connection with the logarithm here [8] :
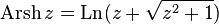 - reverse hyperbolic sine
- reverse hyperbolic sine 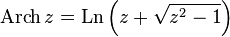 - reverse hyperbolic cosine
- reverse hyperbolic cosine 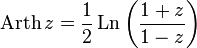 - reverse hyperbolic tangent
- reverse hyperbolic tangent  - reverse hyperbolic cotangent
- reverse hyperbolic cotangent Leibniz and Johann Bernoulli made the first attempts to extend logarithms to complex numbers at the turn of the XVII – XVIII centuries, but they failed to create a holistic theory, primarily because the concept of logarithm was not yet clearly defined [9] . The discussion on this issue was conducted first between Leibniz and Bernoulli, and in the middle of the XVIII century - between D'Alembert and Euler. Bernoulli and D'Alembert believed that should be determined 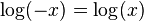 while Leibniz argued that the logarithm of a negative number is an imaginary number [9] . The complete theory of the logarithms of negative and complex numbers was published by Euler in 1747–1751 and essentially does not differ from the modern one [10] . Although the controversy continued (D'Alembert defended his point of view and argued it in detail in an article in his Encyclopedia and in other works), Euler’s approach towards the end of the 18th century was universally accepted.
while Leibniz argued that the logarithm of a negative number is an imaginary number [9] . The complete theory of the logarithms of negative and complex numbers was published by Euler in 1747–1751 and essentially does not differ from the modern one [10] . Although the controversy continued (D'Alembert defended his point of view and argued it in detail in an article in his Encyclopedia and in other works), Euler’s approach towards the end of the 18th century was universally accepted.
In the XIX century, with the development of complex analysis, the study of the complex logarithm stimulated new discoveries. Gauss in 1811 developed a complete theory of the multiplicity of the logarithmic function [11] , defined as the integral of  . Riemann, based on already known facts about this and similar functions, built a general theory of Riemann surfaces.
. Riemann, based on already known facts about this and similar functions, built a general theory of Riemann surfaces.
The development of the theory of conformal mappings showed that the Mercator projection in cartography, which arose before the discovery of logarithms (1550), can be described as a complex logarithm [12] .
Comments
To leave a comment
Comprehensive analysis and operational calculus
Terms: Comprehensive analysis and operational calculus