Polylogarithm is a special function denoted by 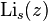 and defined as an infinite power series
and defined as an infinite power series
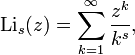
where s and z are complex numbers, and 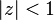 . For other z, a generalization is made using analytic continuation.
. For other z, a generalization is made using analytic continuation.
| Polylogram heights on the complex plane |
|
|
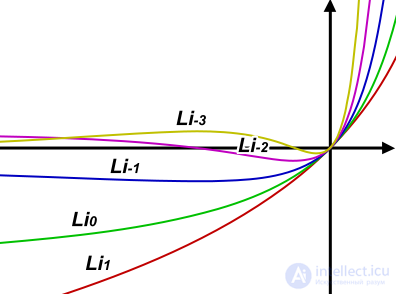
A special case is 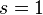 in which
in which 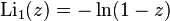 . Functions
. Functions 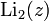 and
and 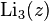 were named dilogarithm and trilogarithm respectively. For polylogarithms of various orders, the ratio
were named dilogarithm and trilogarithm respectively. For polylogarithms of various orders, the ratio
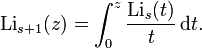
Alternative definitions of the polylogarithm are Fermi-Dirac and Bose-Einstein integrals.
Partial Values
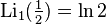
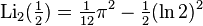
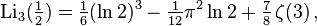
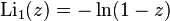
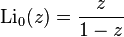
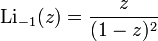
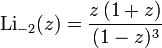
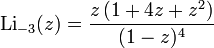
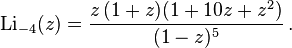
Literature
- Abel NH compuvres complètes de Niels Henrik Abel - Nouvelle édition, Tome II. - Christiania [Oslo]: Grøndahl & Søn, 1881. - P. 189–193. (this 1826 manuscript was only published posthumously.)
- Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. - New York: Dover Publications, 1972. - ISBN 0-486-61272-4.
- (April 1997) "On the Rapid Computation of Various Polylogarithmic Constants" (PDF). Mathematics of Computation 66 (218): 903–913. DOI: 10.1090 / S0025-5718-97-00856-9.
See also
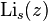 and defined as an infinite power series
and defined as an infinite power series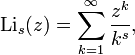
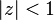 . For other z, a generalization is made using analytic continuation.
. For other z, a generalization is made using analytic continuation.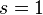 in which
in which 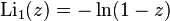 . Functions
. Functions 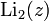 and
and 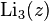 were named dilogarithm and trilogarithm respectively. For polylogarithms of various orders, the ratio
were named dilogarithm and trilogarithm respectively. For polylogarithms of various orders, the ratio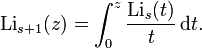

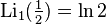
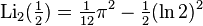
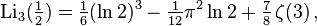
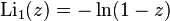
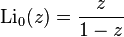
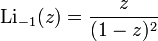
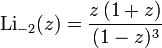
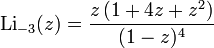
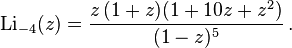
Comments
To leave a comment
Comprehensive analysis and operational calculus
Terms: Comprehensive analysis and operational calculus