Lecture
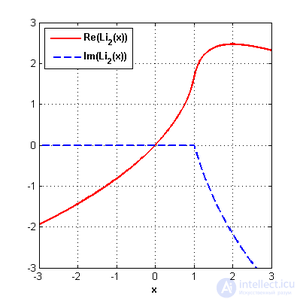
The real and imaginary parts of the function 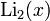
Dilogarithm is a special function in mathematics, which is denoted 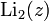 and is a special case of (n = 2) polylogarithm
and is a special case of (n = 2) polylogarithm 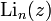 . Dogarithm is defined as
. Dogarithm is defined as
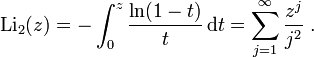
The above definition of the dilogarithm is true for complex values of the variable z . For real values of z = x , this function has a cut along the real axis from 1 to 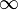 . Usually the value of the function on the section is determined so that the imaginary part of the dilo-log is negative:
. Usually the value of the function on the section is determined so that the imaginary part of the dilo-log is negative:
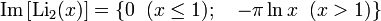
Function 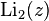 often referred to as Euler's dilogarithm, in honor of Leonard Euler, who considered this function in 1768 [1] . Sometimes the dilogarithm is called the Spence's function , in honor of the Scottish mathematician William Spence ( William Spence , 1777–1815) [2] , who in the early nineteenth century investigated the functions corresponding to
often referred to as Euler's dilogarithm, in honor of Leonard Euler, who considered this function in 1768 [1] . Sometimes the dilogarithm is called the Spence's function , in honor of the Scottish mathematician William Spence ( William Spence , 1777–1815) [2] , who in the early nineteenth century investigated the functions corresponding to 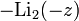 and
and 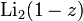 . The name "dilogarithm" was introduced by Hill ( CJ Hill ) in 1828.
. The name "dilogarithm" was introduced by Hill ( CJ Hill ) in 1828.
For dilogarithm, there are a number of useful functional relationships,
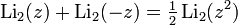
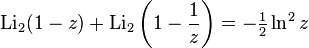
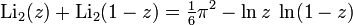
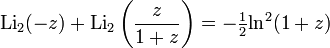
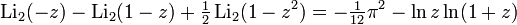
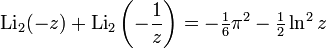
For valid 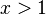 ,
,
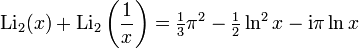
Relations are also known that contain two independent variables — for example, the Hill identity:
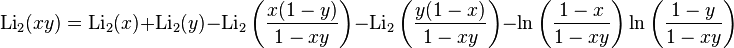
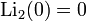
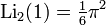
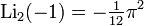
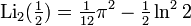
Using the relationship between the functions of x and 1 / x , we obtain
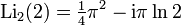
There are also a number of results for arguments related to the golden section. 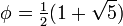 ,
,
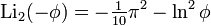
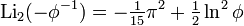
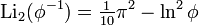
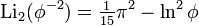
as well as for the logarithm of an imaginary argument,
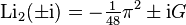
where G is the Catalan constant.
Relations for particular values
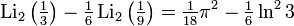
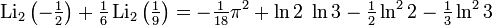
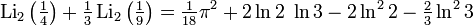
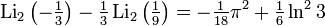
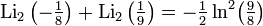
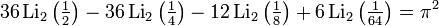
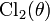
Occurs when considering a dilo-log, whose argument is on a unit circle in the complex plane,
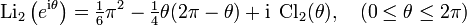
In this way,
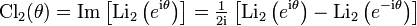
This function is used in the calculation of volumes in hyperbolic geometry, and it is associated with the Clausen function (and hence with the dilogarithm),
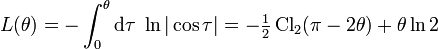
Sometimes a different definition of the Lobachevsky function is used,

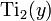
Occurs when considering the imaginary argument's logarithm,
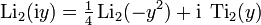
In this way,
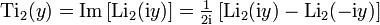
This function is expressed in terms of logs as
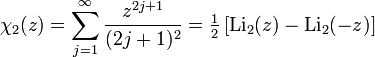
In particular, 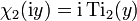 .
.
Comments
To leave a comment
Comprehensive analysis and operational calculus
Terms: Comprehensive analysis and operational calculus