Principles of laser technology

Laser (laser, acronym from light amplification by stimulated emission of radiation), optical quanta generator — a device that converts pumping energy (light, electric, thermal, chemical, etc.) into coherent energy, monochromatic, polarized and narrowly directed radiation flux.

It is 50 years since the appearance of the first lasers, which opened the beginning of a new laser era in the history of the development of science and technology. Indeed, this period can be called a new era, since the dynamics of development, the global use in various areas of human activity, the scale of the impact on the quality of life and the further prospects for expanding the areas of influence of this achievement that have not yet been fully realized allow us to consider laser technology as one of the most remarkable discoveries of the twentieth century.

The creation of lasers is primarily due to deep theoretical developments in the field of quantum physics, electronics, optics of a number of the greatest scientists of the last century: A. Einstein, A. Prokhorov, N. Basov, C. Townes, A. Meiman, J., Gould and many others. Initially, laser radiation with its unique properties was considered primarily as a possible new powerful weapon for defeating manpower and technology. Therefore, the most industrially developed countries have sent enormous resources to the development of the new industry, which made it possible to discover other promising areas using laser technology and technology. In Ukraine, the first studies on the creation of lasers were initiated at the Institute of Physics, the Institute of Semiconductor Physics and other organizations of the Academy of Sciences of Ukraine. The first studies on the use of laser radiation for processing materials were started at the Kiev Polytechnic Institute (KPI) in 1964, and in 1967 the world's first monograph in this area was published at Tekhnika publishing house (Kiev): Kartavov S. A., Kovalenko V.S. "The use of optical quantum generators (laser) for technological purposes."

The first solid - ruby ​​lasers generated radiation in a pulsed mode with a very low frequency and energy per pulse. Their efficiency was also very small (tenths of a percent). Therefore, they were used mainly for flashing precision holes of small diameter in difficult-to-cut materials. Later, more efficient neodymium glass lasers appeared, as well as CO2 gas lasers. Gas lasers generate both high frequency pulsed radiation and continuous radiation. The radiation power is already measured in hundreds of watts and tens of kilowatts. Kpd these lasers do not exceed 10%, so the equipment is rather cumbersome due to the overall and powerful cooling systems. Fully reliable excimer lasers, generating radiation in the ultraviolet region of the electromagnetic spectrum, have been developed. In recent years, new developments of diode lasers with high efficiency have been widely adopted. They are also used for pumping solid-state lasers instead of less efficient gas-discharge pump lamps. Powerful (up to several kW) diode lasers have already been widely used in the technology, allowing to create compact equipment for industrial purposes. The most significant development of recent times can be considered the creation of a wide range of fiber-optic lasers with a power of up to several kW with efficiency. up to 60% and higher. Such modern laser systems are built into robotic technological complexes and are widely used in various industries - electronic, automotive, aerospace, etc.

Since its invention, lasers have proven to be “ready-made solutions to not yet known problems.” Due to the unique properties of laser radiation, they are widely used in many branches of science and technology, as well as in everyday life (compact disc players, laser printers, barcode readers, laser pointers, etc.). In industry, lasers are used for cutting, welding and soldering parts from various materials. High radiation temperature allows welding materials that cannot be welded using conventional methods (for example, ceramics and metal). The laser beam can be focused to a point with a diameter of the order of microns, which allows its use in microelectronics (the so-called laser scribing). Lasers are used to obtain surface coatings of materials (laser doping, laser cladding, vacuum laser deposition) in order to increase their wear resistance. Laser marking of industrial designs and engraving of products from various materials has also received wide application. Laser processing of materials does not affect them mechanically; therefore, only minor deformations occur. In addition, the entire process can be fully automated. Laser processing is therefore characterized by high accuracy and performance.

Lasers are used in holography to create the holograms themselves and to obtain a gologaphic three-dimensional image. Some lasers, such as dye lasers, are capable of generating monochromatic light of almost any wavelength, while radiation pulses can reach 10–16 s and, consequently, enormous powers (the so-called giant pulses). These properties are used in spectroscopy, as well as in the study of nonlinear optical effects. Using a laser, we were able to measure the distance to the moon with an accuracy of a few centimeters. The laser location of space objects clarified the values ​​of a number of fundamental astronomical constants and contributed to the refinement of space navigation parameters, expanded the understanding of the structure of the atmosphere and the surface of planets of the solar system. In astronomical telescopes equipped with an adaptive optical system for correcting atmospheric distortions, a laser is used to create artificial reference stars in the upper atmosphere .

The use of lasers in metrology and measurement technology is not limited to measuring distances. Lasers find here a wide variety of applications: for measuring time, pressure, temperature, flow rate of liquids and gases, angular velocity (laser gyroscope), concentration of substances, optical density, various optical parameters and characteristics, in vibrometry, etc.

Ultrashort laser pulses are used in laser chemistry to initiate and analyze chemical reactions. Here, laser radiation allows for accurate localization, dosage, absolute sterility and high rate of energy input into the system. Currently various laser cooling systems are being developed. The possibility of using controlled fusion by means of lasers is under development. Lasers are also used for military purposes, for example, as means of guidance and aiming. Consider the options for creating on the basis of high-power lasers combat systems to protect air, sea and land-based

In medicine, lasers are used as bloodless scalpels, used in the treatment of ophthalmologic diseases (cataracts, retinal detachment, laser vision correction, etc.). Also widely used in cosmetology (laser hair removal, treatment of vascular and pigmented skin defects, laser peeling, removal of tattoos and age spots)

Currently, the so-called laser connection is rapidly developing. It is known that the higher the carrier frequency of a communication channel, the greater its bandwidth. Therefore, radio communication tends to move to shorter and shorter wavelengths. The light wavelength is on average six orders of magnitude less than the wavelength of the radio band, therefore, by means of laser radiation, a much larger amount of information can be transmitted. Laser communication is carried out both in open and in closed light-guide structures, for example, in optical fiber. Light due to the phenomenon of total internal reflection can spread over it over long distances, almost not weakened by the Laser, which provides the maximum power in a pulse, at the moment is the Texas petawatt laser (1.1 PW).

Even this small list of achievements over the past period indicates that laser technology is still far from saturation, intensive development continues successfully and its further wide spread is expected in all areas of human activity

Development of the theoretical principles of laser technology

The study of the principles of laser technology follows from an excursion into the history of the study of the nature of light. The first ideas about the nature of light were laid in ancient times. The Greek philosopher Plato (427–327 BC) created one of the first theories of light. Euclid and Aristotle (300-250 BC) empirically established such basic laws of optical phenomena as rectilinear propagation of light and independence of light beams, reflection and refraction. Aristotle first explained the essence of vision.

Despite the fact that the theoretical positions of the ancient philosophers, and later scientists of the Middle Ages, were insufficient and contradictory, they contributed to the formation of correct views on the essence of light phenomena and laid the foundation for the further development of the theory of light and the creation of various optical devices. With the accumulation of new research on the properties of light phenomena, the point of view on the nature of light has changed. Scientists believe that the history of the study of the nature of light should begin with the XVII century.

In the Middle Ages, the empirical rules for constructing images given by lenses became known. In 1590 Z. Jansen built the first microscope, in 1609 G. Galileo invented the telescope. The quantitative law of refraction of light when passing the interface between two media was established in 1620 by V. Snellius. Mathematical recording of this law in the form 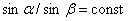, belongs to R. Descartes (1637). He tried to explain this law on the basis of the corpuscular theory. Subsequently, the formulation of the Fermat principle (1660) completed the foundation for the construction of geometric optics. Further development of optics is associated with the discoveries of diffraction and interference of light (F. Grimaldi, 1665), double refraction (E. Bartolin, 1669) and with the works of I. Newton, R. Guka, H. Huygens.

At the end of the 17th century, two powerful theories of light — the corpuscular (Newton – Descartes) and the wave (Hook – Huygens) —had based on centuries-old experience and the development of light. H. Newton developed a coherent theory of expiration. Light - corpuscles emitted by bodies and flying at great speed. Newton naturally applied the laws of mechanics formulated by him to the analysis of the movement of light corpuscles. From these ideas he easily deduced the laws of reflection and refraction of light.

However, from Newton's reasoning it followed that the speed of light in matter is greater than the speed of light in a vacuum: .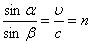

In addition, in 1666, Newton showed that white light is composite and contains "pure colors", each of which is characterized by its refractivity (Fig. 7.12), i.e. gave the concept of light dispersion. This feature was explained by the difference in the mass of corpuscles.

At the same time in the XVII century. (along with the concept of Descartes - Newton) developed the opposite, the wave theory of Hooke - Huygens that light is the process of propagation of longitudinal deformations in a medium that permeates the whole body - in the world ether.

By the end of the XVII century. a very peculiar position has developed in optics. Both theories and theories explained the main optical laws: the straightness of propagation, the laws of reflection and refraction. Further attempts to more fully explain the observed facts led to difficulties in both theories.

Huygens could not explain the physical reasons for the presence of different colors and the mechanism for changing the speed of light in the ether, which penetrates various media.

It was difficult for Newton to explain why when two media fall on the boundary, both partial reflection and refraction, as well as light interference and dispersion, occur. However, the great authority of Newton and the incompleteness of the wave theory led to the fact that the entire XVIII century. passed under the sign of corpuscular theory.

The beginning of the XIX century. It is characterized by the intensive development of the mathematical theory of coles and waves and its application to the explanation of a number of optical phenomena. In connection with the works of T. Jung and O. Fresnel, the victory temporarily shifted to wave optics.

· 1801 T. Jung formulates the principle of interference and explains the colors of thin films.

· 1818 O. Fresnel explains the phenomenon of diffraction.

· 1840 O. Fresnel and D. Argo investigate the interference of polarized light and prove the transverse nature of light lines ***.

· 1841 O. Fresnel builds the theory of crystal optics *** ing.

· 1849 A. A. Fizeau measured the speed of light and calculated the refractive index of water using the wave theory 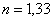that coincided with the experiment.

· 1848 M. Faraday discovered the rotation of the plane of polarization of light in a magnetic field (Faraday effect).

· 1860 J. Maxwell, based on the discovery of Faraday, came to the conclusion that light is electromagnetic waves, not elastic.

· 1888 G. Hertz experimentally confirmed that the electromagnetic field propagates at the speed of light with.

· 1899 P.N. Lebedev measured the pressure of light.

It seemed that the dispute was completely resolved in favor of the wave theory of light, since in the middle of the XIX century. facts were found indicating a connection and analogy between optical and electrical phenomena. Faraday, Maxwell and other scientists have shown that light is a special case of an electromagnetic wave with 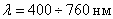. Only this interval of wavelengths affects our eyes and is the actual light. But longer and shorter waves have the same nature as light.

However, despite the huge advances in the electromagnetic theory of light, by the end of the XIX century. new facts began to accumulate that contradicted the wave theory of light. The wave theory could not explain the distribution of energy in the emission spectrum of an absolutely black body and the phenomenon of the photoelectric effect, which, in 1890, was studied by A.G. Stoletov.

At the turn of the XIX and XX centuries, Lord Kelvin enthusiastically proclaimed a toast to the health of nineteenth-century physicists who built the magnificent building of physics, and left the twentieth century only the opportunity to refine the decimal places in world constants introduced in the XIX century. At the same time, in his lecture, “read in the Royal Society on April 27, 1900, with the title“ The Clouds of the 19th Century Over the Dynamic Theory of Heat and Light, ”he shrewdly remarked:“ The beauty and clarity of the dynamic theory taking heat and light for the forms of movement, currently eclipsed by two clouds. ”

The first Kelvin cloud is associated with the well-known Michelson-Morley experiments, the second concerns the contradiction between the energy distribution according to Maxwell-Boltzmann and experimental data on the specific heats of gases, taking into account collective and rotational degrees of freedom. The second problem was related to the black body radiation problem. Now we know that from the first “cloud” the theory of relativity further grew, and from the second - modern quantum physics. Consider the early stage of development of the second "cloud". Her story is connected with the discovery by Planck of a universal physical constant named after him. The discovery of Planck's constant was the result of the resolution of difficulties and contradictions in the explanation of the experimental facts related to the problem of blackbody radiation.

In 1859, the German physicist Gustav Kirchhoff (G Kirchhoffi 1824-1887) discovered an important law that played a major role in the development of ideas about the radiation of heated bodies.

Using the general laws of thermodynamics, Kirchhoff showed that in a state of thermal equilibrium, regardless of the substance and device of the body (device), the ratio of the emissivity of a heated body to its absorption capacity is a universal function. This function, which is called the Kirchhoff function K (v, T), is determined only by the radiation frequency v and the absolute temperature T. The Kirchhoff law was based on firmly established general principles of thermodynamics, in particular, on the impossibility of a second-type perpetuum mobile, i.e. . impossibility of obtaining energy due to the transfer of heat from a cold body to a hot body. Like the laws of thermodynamics, the Kirchhoff law is of a general nature. After the establishment of this law, the problem arose of finding the Kirchhoff function, or its related function

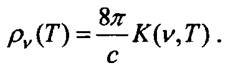
This function is called the spectral density of radiation. It has the meaning of the energy density of radiation per unit frequency interval. If we sum the value of pv over all frequencies that characterize radiation, then we obtain the radiation energy density, that is, the radiation energy per unit volume. The emissivity is maximum for those bodies that absorb all the energy falling on them. Kirchhoff called such bodies absolutely black in 1860. Practically the black body can be made in the form of a cavity with impenetrable uniformly heated walls. Some similarity of this type of radiation trap is a room with one window, especially a mirror one: if you look into the room through a window, the room appears dark because the light penetrating through the window is almost completely absorbed by the walls and reflected by the glass and only a small part of it goes out again out. Inside the cavity, as a result of multiple emission and absorption of radiation at a given temperature, thermal equilibrium is established. This is black body radiation. It can be observed by making a small hole in the cavity wall. The energy emitted through this hole is considered equal to the energy of the black body radiation at a given temperature. It was rather difficult to measure the spectral density of radiation. One of the first such measurements was carried out by the American physicist Samuel Langley (S. Langley, 1834-1906), who for this purpose invented a special device - a bolometer. In 1886, he obtained data on the distribution of energy in the thermal radiation spectrum of sources blackened with soot in the far infrared region (I = 5.3 µm).

At the same time, German physicists under the direction of Otto Lummer (O. Lummer, 1860-1925) created highly sensitive radiation receivers, with the help of which the accuracy of measurements was significantly increased. They also developed various blackbody models. In 1893-1894, the German physicist Wilhelm Wien (W. Wien, 1864-1928) came to the conclusion that the spectral density of blackbody radiation should be described, in general, by the formula pv (T) = v3F (v / T), F ( v / T) is a function whose specific form remained uncertain at that time. But already from such a general expression it followed that the distribution curve of the spectral density of blackbody radiation should have a maximum, and the wavelength that corresponds to this maximum is inversely proportional to the absolute body temperature: R ^ T = Const = 0.2898 cm-deg. Thus, the law of displacement of wine was discovered. Using the hypothesis of the Russian physicist V. A. Michelson (1860-1927) that the frequency distribution of radiation energy is similar to the velocity distribution of gas molecules, Win in 1896 proposed an empirical formula that determined the spectral density of radiation already in an explicit form.

For the discovery of the laws of radiation in 1911, Win was awarded the Nobel Prize.

In 1899-1900, Otto Lummer, Ferdinand Kurlbaum (F. Kurlbaum, 1857-1927), Ernst Pringsheim (E. Pringsheim, 1881-1964) and Heinrich Rubens (J. Rubens, 1865-1922) measured the spectral density of the radiation energy. In fig. 2.1 shows the dependence of the spectral radiation density on the wavelength (in microns) at different temperatures. From the experiments it followed that the Wien formula is valid only in the region of short waves (or at sufficiently low temperatures).

In 1900, Lord Rayleigh (John Strett, J. Rayleigh, 1842-1919), on the basis of the well-known law of kinetic theory of the uniform distribution of energy over degrees of freedom, obtained another formula for the distribution of energy in the spectrum of an absolutely black body: pv (T) = Cv2T, where C - some value that does not depend on temperature. The conclusion of this formula was further clarified by James Jean (J. Jeans, 1877-1946).

Fig. 2.1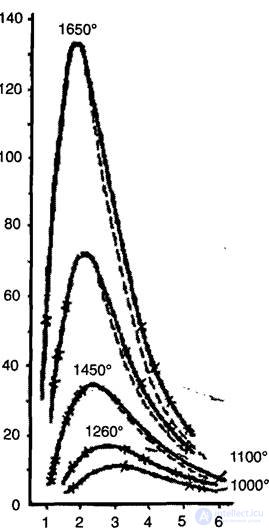

The experiment showed that in the region of long waves (or at sufficiently high temperatures) the spectral density of radiation is proportional to temperature, which corresponds to the Rayleigh – Jeans formula. At first they tried to apply this formula to the entire frequency range (or wavelengths), which clearly led to an absurdity. Indeed, summation over all frequencies from zero to infinity leads to the fact that the radiation energy density is infinitely large, which is physically meaningless. From the Rayleigh – Jeans formula, it follows that most of the energy in the spectrum of thermal radiation falls on the shortwave, or, as they say, ultraviolet part, which contradicts the experiment. This contradiction is one of the founders of the quantum theory.

Paul Ehrenfest (P. Ehrenfest, 1880–1933) called the “ultraviolet catastrophe” or Rayleigh – Jeans paradox. On this occasion, the patriarch of classical physics, Hendrik Lorenz (I Lorentz, 1853-1928) noted that "the equations of classical physics were unable to explain why a dead furnace does not emit yellow rays along with the emission of large wavelengths."

Among many physicists of the late 19th century who tried to find an expression for the pv (or px) spectral function that would be consistent with the experimental data was Max Karl Ernst Ludwig Planck (M. Planck, 1858-1947).

Max Planck was a student of Helmholtz and Kirchhoff. He studied at the University of Munich. When choosing a profession, he cole *** between the ancient philology, physics and music. Professor of the University of Munich Philip von Jolly (von Jolly), believing that after the establishment of the law of conservation of energy, other discoveries are not expected, did not advise Planck to do physics. Fortunately, young Plank did not follow this advice. His works relate to the theory of thermal radiation, thermodynamics, the theory of relativity, quantum theory, the history of physics. He introduced the term "theory of relativity." Planck died in October 1947 in Göttingen.

Planck for the first time managed to get a formula explaining all the properties of thermal radiation of a black body. Knowing the flaws of the Wine formula, Planck persistently tried to improve it. Many years later, he recalled that the famous formula was found by him on Sunday, October 7, 1900. According to him, on this day his colleague, experimental physicist Rubens, came to visit him. During the conversation, Rubens talked about recent experiments, from which it followed that for short wavelengths the radiation intensity is well described by Wien's law, and for long waves the intensity is proportional to temperature. That same evening, according to Planck’s testimony, he obtained an interpolation formula for the pL function, which at small wavelengths passed into the Wien formula, and in the case of large wavelengths, contained a direct proportional dependence on temperature. Here is the formula: rL = -.

The constants c, and c2 must be determined by comparison with experimental data. At that time, there was already a graphical method “isochromat”, which was developed by Friedrich Paschen (F. Paschen, 1865-1947). This method made it possible to carefully check the theoretical expressions for the energy distribution in the spectra of heated bodies, in particular, to determine the constants included in the formulas when the temperature changes.

Planck presented his formula in the report “On Improving the Wien Formula for Spectral Distribution” at the meeting of the German Physical Society on October 19, 1900 (Verhlandl. Dtsch. Phys. Ges. 2, 202-204). “The next morning,” Planck later recalled, “my colleague Rubens found me and told me that after the meeting was closed that night, he carefully compared my formula with his measurements, and everywhere a satisfactory coincidence was found ... More recent the measurements confirmed again and again the formula for the radiation and, moreover, the more precisely, the more subtle methods were used. ” Planck discovered his formula by ingeniously guessed interpolation.

As Planck later recalled, this was so: since, according to Kirchhoff, the laws of equilibrium radiation do not depend on the shape and material of the cavity, he used a cavity model that consists of radiating and absorbing atoms, represented as oscillators of different frequencies. Then he applied the first law of thermodynamics to the oscillator, considering the volume of the system to be constant: du = Tds. Here s is the entropy of the oscillator, and its energy. According to Planck, the majority of physicists of that time tried to find the function pv as a function of temperature to coordinate with the experimental data, and he persistently and purposefully investigated the dependence of entropy on energy, and in this direction he had no competitors. As Planck later recalled, he "... suspected the existence of a deep connection between entropy and energy." Indeed, in 1899, he showed that when the law of displacement of wine is taken into account, entropy

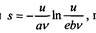the oscillator is related to its energy by the ratio, where a and

b - constants, e - the base of the natural logarithm. He found

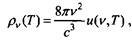same formula

where u (v, T) is the mean oscillation energy

The frequency controller v is in a state of thermodynamic equilibrium with black radiation at temperature T. Considering the change in the entropy of an oscillator as its energy increases and the energy of the radiation changes, Planck found that the change in entropy is determined by the second

"

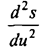derivative which should be negative. On this occasion

he later wrote: “Since the irreversibility of the energy exchange between some oscillator and the excited radiation is of crucial importance to the derivatives of the oscillator's entropy in its energy, I calculated the value of this quantity for the case when the Wien’s law, which was then the center of attention, and came to the remarkable result that in this case the reciprocal of this derivative is proportional to the energy. ” Indeed, it follows from the formulas written above that d2s / du2 = -l / avu. This ratio is obtained using the Wien formula. Further, Planck took into account the experimental fact that at long wavelengths the radiation intensity is proportional to temperature. This allowed us to assume that in this case u = CT, where C is a certain quantity that does not depend on temperature. Hence, finding the entropy s = C \ pi, it is easy to calculate the second derivative of the entropy. Brilliant guess and

k Planck was that he considered these two expressions for the second derivatives of entropy as limiting cases of a more general formula

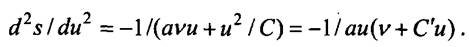As Planck noted in his report, “Among all the proposed expressions, one deserves special attention; it is, by simplicity, closest to the Wine formula and, since the latter is insufficient to describe all the observations, it seems worthy of careful consideration. This expression is obtained by using the expression 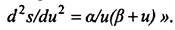So Planck came to his interpolation formula. Next, integrating

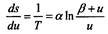Planck obtained an equation from which it immediately follows.

formula 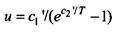According to the law of wine 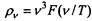and since, as Planck showed, the spectral density and the average energy of the oscillator

ra are related by 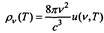then, in general, the average energy of an oscillator should be determined by the formula of the form u = vF (v / T). Comparing this expression with the previously obtained formula, Planck found that 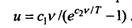So Planck got the above formula with two constants. In the future, instead of the constant c1 and c2, Planck introduced new constant h and k.

Thus, Planck found a surprisingly accurate formula for the distribution of energy in the black body spectrum. However, he understood that this formula was “only happily discovered by interpolation formula, therefore, from the very day it was established before me,” as he wrote later, “the task arose of finding Re's true physical meaning, and this problem led me to consider the relationship between entropy and probability in the spirit of developing the ideas of Boltzmann. It was on this path, after several weeks of the most intensive work in my life, that the darkness cleared up, and the light of new distances began to shine before me. ” On December 14, 1900, Max Planck delivered a new report in the German Physical Society “On the Theory of the Law of Energy Distribution in the Normal Spectrum”, in which he first reported on the energy elements and quantum of action introduced by him (Verhlandl. Dtsch. Phys. Ges. 1900, 2 237-245). This day is rightly considered the birthday of quantum theory. Somewhat later, Planck presented the results of his work in the article "On the law of energy distribution in the normal spectrum" (Max Planck. Annalen der Physik, 4, S. 55, 1901. Translation of these articles: M. Planck, Selected Works. M .: Nauka, 1975).

Using the available experimental data at the time, Planck determined

values ​​of two universal constants: quantum of action h = 6.55 Yu-27

erg e, which is known as Planck's constant, and k = 1.346-10 16 erg / hail, which was not considered in physics before Planck, and which was later called the Boltzmann constant. On this occasion, Planck wrote many years later: ".. This constant is often referred to as the Boltzmann constant, although Boltzmann himself never introduced it, as far as I know this strange circumstance is explained by the fact that Boltzmann, as it seems, follows from his random statements, absolutely did not think about the possibility of accurately measuring this constant. "

Planck also calculated the number of Loshmidt and the electron charge, the values ​​of which were consistent with the data available at that time. This, of course, could not be accidental and testified to the validity of the quantum hypothesis.

At low radiation frequencies (as compared with the energy of thermal motion), it follows from Planck’s formula that the spectral radiation density is proportional to temperature: pv «(8nv / s) kT. This is fully consistent with the Rayleigh-Jeans formula. In the case of high frequencies (short wavelengths), the Wien formula follows. Thus, the "ultraviolet catastrophe" is eliminated. It, in fact, arose from the fact that the Rayleigh-Jeans formula was improperly distributed over the entire frequency range of radiation. For any frequency, the Planck formula is valid, which does not contain any paradox and is completely consistent with the experimental data.

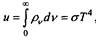The integrated radiation density calculated using the form

ly Planck turns out to be finite: where is the constant

a = 1.08-48; / c3. This corresponds exactly to the Stefan – Boltzmann law known in thermodynamics.

So, Planck showed that the “energy element” is equal to s = hv, i.e., that the energy of the oscillator is transferred by quanta — discrete portions Av. It was a revolutionary step in the development of physics. As Henri Poincare wrote, Planck’s theory, according to which “... physical phenomena no longer obey the laws expressed by differential equations, is without any doubt the greatest and most profound revolution that natural philosophy has undergone since Newton's time.” The idea of ​​energy quanta contradicted both mechanics and electrodynamics, but Planck did not see any other way out. Considering the meaning of the constant action introduced by him, Planck came to the conclusion that this constant "... was either a fictitious value, and then the entire derivation of the radiation law was basically false and was just an empty game of formulas without meaning, or the derivation of the radiation law rests on some physical reality, and then the quantum of action must acquire fundamental importance in physics and means something completely new and unheard of, which should produce a revolution in our physical thinking, based on Leib Itza and Newton discovered calculus, on the hypothesis of the continuity of all causal relations ... I immediately began to try in any way to enter the quantum quences within the framework of the classical theory. But this value stubbornly and persistently resisted all such attempts. While we had the right to consider it as infinitely small, that is, at relatively high energies and long periods of time, everything was in perfect order. But in the general case, a crack appeared here and there, all the more pronounced, the faster we saw. ” Planck called the new fundamental constant of physics "the mysterious ambassador from the real world."

To explain the mechanism of propagation of "elements" or "; units of energy," as they were then called, two options were possible: these elements of energy after radiation retain their individuality during propagation, or each emitted element is scattered in space as it moves away from the source. The first option is not compatible with classical optics, which is based on the wave nature of the propagation of electromagnetic radiation. Planck, despite the revolutionary nature of his discovery, brought up in the spirit of the old, kind classical physics, was his zealous keeper, and, like many at the time, could not accept the fact that a well-tested wave theory has a limited range of applicability. Therefore, at first he believed that the process of emission and absorption occurs in discrete portions, and the radiation itself is continuous. In contrast to Planck, Einstein was the first to realize the revolutionary nature of the quantum idea introduced by Planck and developed it further. Evaluating the value of the discovery of Planck, Einstein wrote: “.. the Planck radiation law gave the first exact definition of the absolute values ​​of atoms, independently of other assumptions. Moreover, he convincingly showed that, in addition to the atomistic structure of matter, there is a kind of atomistic structure of energy, governed by the universal constant introduced by Planck. This discovery became the basis for all research in the physics of the 20th century, and since then has almost completely determined its development. Without this discovery, it would be impossible to establish a true theory of molecules and atoms and energy processes that control their transformations. Moreover, it destroyed the skeleton of classical mechanics and electrodynamics and set the task for science: to find a new cognitive basis for all physics. ”

Planck himself for a long time tried using various hypotheses to explain the propagation of radiation based on wave representations, and it was only under the pressure of experimental facts that he was forced to give up his attempts. Evaluating his work in this direction, Planck subsequently wrote: “My vain attempts to somehow introduce a quantum of action into the classical theory continued for a number of years and cost me a lot of work. Some of my colleagues saw this as a kind of tragedy. But I had a different opinion about this, because the benefits I gained from this in-depth analysis were very significant. After all, now I knew for sure that a quantum of action plays a much larger role than I initially was inclined to consider ... ", the introduction of a quantum of action" ... meant a break with the classical theory, a break was more radical than I had originally intended. " And in his Nobel speech on July 2, 1920, Planck said: “When I look back at the times of 20 years ago, the times when for the first time a number of experienced facts began to show the concepts and magnitude of a physical quantum of action, and a long, winding path that eventually led to its discovery, it all seems to me now a new illustration to the long-spoken words of Goethe, that a person is mistaken as long as he has aspirations. ” Of course, Planck's efforts were not in vain, and in one of his works in 1911, Planck obtained a result that turned out to be extremely important in physics: he showed that at absolute zero temperature, the average energy of an oscillator does not vanish, but is equal to hv / 2. This value was later called the "zero energy" of the oscillator, or the energy of zero oscillations. Developing the ideas of Planck, the German physicist Walter Nernst (W. Nernst, 1864–1941) in 1916 suggested that the ether could be continuously filled with “zero-point energy,” corresponding to an absolute zero temperature.

In 1918, for the discovery of a quantum of action, Max Planck was awarded the Nobel Prize in Physics.

Planck’s quantum idea, as often happens with revolutionary ideas, was not immediately accepted by his contemporaries. In this respect, the memories of one of the founders of quantum mechanics Max Born (M Born, 1882-1970) are characteristic: “How were these ideas accepted? I will allow myself to talk about my own experiences. In Göttingen, as I recall, I have not heard anything about quanta; also in Cambridge, where in the spring and summer of 1906 I had listened to the lectures of JJ Thomson and Larmor for several months and passed an experimental circle in the Cavendish laboratory. Only when I arrived in Breslau in the autumn of 1906 to Lummer and Pringsheim, did I get into a real quantum atmosphere. For both of them made a significant contribution to the experimental study of black radiation. But although Planck’s formula was at the center of the discussion, those who were discussing were inclined to consider Planck’s hypothesis about quantizing the oscillator energy as a preliminary working hypothesis, and Einstein’s light quanta didn’t take it seriously ... ” Similarly, according to the memoirs of Max von Laue (Max von Laue, 1879-1960), in 1902 he "... went to Planck's lecture on theoretical optics. I knew him as the author of a thermodynamics textbook, and I knew that he was very involved in optics. But I did not know anything about his main great deed — the discovery in 1900 of the law of radiation and the quantum theoretical substantiation of it; these were then not yet recognized and therefore little known studies. ” And Lorenz, in his book The Theory of Electrons, published in 1909, wrote about quanta: “There is undoubtedly a significant amount of truth in this theory. Of course, it did not in any way serve to uncover the mechanism of phenomena; It should also be recognized that it is very difficult to find an excuse for such an idea of ​​the distribution of energy in portions of finite size that are not even equal to each other. And in the first edition in 1904 of Jeans’s book The Dynamic Theory of Gases, Planck’s law was not even mentioned. Moreover, at that time, among the experimenters, mutual criticism of the accuracy of the measurement results and their alignment with the Planck formula developed. However, the full agreement between the experimental results and the Planck formula was soon recognized.

In 1905, Einstein, in his work “On a heuristic point of view concerning the origin and transformation of light,” suggested that “energy elements” have a special individuality and introduced the hypothesis of light quanta. In his work, Einstein wrote: “I really think that experiments concerning black body radiation, photoluminescence, the appearance of cathode rays when illuminated with ultraviolet rays, and other groups of phenomena associated with the appearance and transformation of light are better explained by the assumption that the energy of light is distributed discretely in space ... The energy of a light beam that has left a certain point out of them is not distributed continuously in an ever-increasing volume, but is added up from a finite number of spaced indivisibles in space x energy quanta absorbed or arising only wholly ... The above arguments, in my opinion, do not refute Planck’s radiation theory; on the contrary, they seem to show that Planck in his radiation theory introduced into physics a hypothetical element light quantum hypothesis.

To come to this conclusion, Einstein considered the entropy S

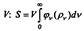black radiation occupying the volume, where

entropy, pvdv is the energy per unit volume of radiation in the frequency range (v, v + dv). Since the entropy of black radiation is maximum at

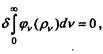given energy (and constant volume), then, provided

that pvdv - 0 Spvdv = 0.

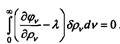Introducing the uncertain Lagrange multiplier, these relations can be written in the form:

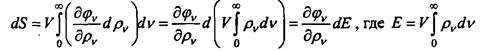arbitrarily, it follows that the derivative does not depend on frequency. Next, Einstein calculates the entropy increment dS at a constant volume, when the temperature has reversibly changed to dT:

I

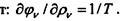Since the process is reversible, and the volume is constant, then dE = TdS. From here and from the previous equality follows:. Determining 1 / T

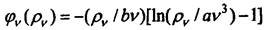from the law of wine, you can find the ratio:.

Hence, after integration, taking into account the condition q> v = 0 for pv = 0,

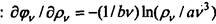follows:

The radiation energy Ev in the unit frequency interval in the volume K is equal to Ev-V pv.

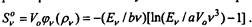The entropy of this radiation The entropy of the equilibrium radiation of the same energy in a different volume V0 is equal. Thus, the difference

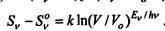entropy is equal to. Here, the constant b according to Planck is replaced by h / k. According to Boltzmann, the entropy difference of states 1 and 2 is proportional to the natural logarithm of the ratio of the number of complexes of these states, i.e. the logarithm of the relative probability of state 1 to state 2. From the last relation it follows that this probability

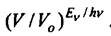equals

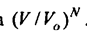Next, we consider an ideal gas consisting of N molecules in a volume V0. It is not difficult to determine the probability that all these / V molecules at some instant of time will randomly gather in the volume V

independence of movement of molecules this probability is equal

Comparing these two expressions for probabilities, Einstein came to the conclusion: “Low-density monochromatic radiation within the range of applicability of the Wien radiation law in the sense of the theory of heat behaves as if it consists of energy quanta independent of each other, hv”. And further, "It begs the question, is not the law of the emergence and transformation of light such as if light consists of similar energy quanta?"

Einstein criticized Planck’s conclusion for his famous formula (A. Einstein, Annalen der Physik. 20, S. 1, 1906; Collection of scientific papers, T. 3. p. 128). He showed that this conclusion is inconsistent, since Planck simultaneously accepted and rejected classical electrodynamics. In fact, Planck, on the one hand, used the formula for the spectral radiation density pv (T) = and (y, T), the structure obtained by him

with

It is based on classical electrodynamics, where it is believed that the oscillator energy changes continuously. On the other hand, when statistically considering the interaction between oscillators with different eigenfrequencies, Planck arrived at the formula and = hv / (ehvlkT -1), while deriving which the same oscillator energy was considered as a discrete quantity that takes only values ​​that are multiples of hv.

Without denying the validity of Planck’s formula itself, Einstein saw in the inconsistency of its derivation a stimulus for the further development of the theory of radiation. A deep analysis of this problem led Einstein to the hypothesis about light quanta.

But Einstein did not limit himself only to the hypothesis of light quanta. First of all, he applied the idea of ​​light quanta to explain the photoelectric effect. Heinrich Hertz (J. Hertz, 1857-1894) accidentally discovered this effect in 1887. He investigated the propagation of electromagnetic waves from a radiating resonator to a receiver. To better see the slipping spark in the radiator, Hertz closed the receiver with a screen. Then it was found that the spark slips at a lower voltage between the electrodes. As it turned out, the reason for this was the lighting of the screen with the light of an electric arc. At that time, Hertz was completely fascinated by the evidence of the existence of electromagnetic waves predicted by Maxwell. Therefore, the discovered effect did not interest him. This effect, called photoelectric or simply photoelectric effect, was rediscovered in 1888 by Wilhelm Galvax (W. Hallwachs, 1859-1922), Augusto Rigi (A. Righi, 1850-1921) and A. G. Stoletov (1839-1896). Galvax showed that when illuminated with ultraviolet radiation, the metal plate is charged positively. Rigi first observed a photoelectric effect in the case of dielectrics (ebonite, sulfur) and proposed the term “photocell”. The first photocell created and applied it to the Stoletov practice. He also discovered one of the laws of the photoelectric effect — the direct proportionality of the photocurrent force to the intensity of the incident light, and discovered a photocurrent of saturation. In 1899, JJ Thomson and Lenard determined the specific charge of particles emitted from the surface of the illuminated body. It turned out to be the same as for cathode rays. So it was proved that electrons are emitted from the illuminated surface. In 1902, Lenard found that the energy of electrons emitted completely does not depend on the intensity of the incident light and is directly proportional to its frequency. This fact cannot be explained on the basis of classical representations. Indeed, according to the classical ideas, an electron in a light field makes collisions, the amplitude of which should increase with increasing wave intensity. Then, naturally, the number of electrons capable of escaping from the surface of the body should grow. This, however, is not observed.

Using the hypothesis about light quanta, Einstein in the eighth paragraph of the same article of 1905 obtained the energy balance equation with a photoelectric effect:

Emax = hv-W,

where Yesh is the maximum energy of the outgoing electrons, W is the work function, that is, the energy required to remove an electron from a substance. From this formula it follows that the maximum energy of photoelectrons depends linearly on the frequency, in accordance with the result of Lenard, and the angle of inclination of the straight line £ max (y) does not depend on the substance and is determined only by Planck's constant. Thus, for the first time, the universal character of Planck’s constant was shown, which, as it turned out, defines patterns in completely different physical phenomena.

Planck strongly opposed Einstein's hypothesis. In 1911, he wrote: “When you think about the full experimental confirmation that Maxwell’s electrodynamics obtained in the study of even the most complex interference phenomena, when you think of the extraordinary difficulties that all theories will have to face in explaining electrical and magnetic phenomena, From this to the throdynamics, you instinctively dislike any attempt to break its foundation. For this reason, we will further put aside the hypothesis of "light quanta", especially since this hypothesis is still in its embryonic state. We assume that all phenomena that occur in a vacuum exactly correspond to Maxwell’s equations and have no relation to the constant A. Niels Bohr adhered to the same opinion even in 1923. He wrote: “Although this point of view is of great importance for understanding some classes; phenomena, such as the photoelectric effect, from the standpoint of quantum theory, the hypothesis cannot be all considered It is well known that this hypothesis leads to insurmountable difficulties in explaining interference phenomena, which represent the main tool in the study of radiation properties. In any case, it can be argued that the underlying principle of the light quanta hypothesis excludes the possibility of thinking the concept of frequency v, which plays a major role in this theory. Therefore, the light quanta hypothesis is unsuitable to provide a general picture of the processes, which could include all Bathiness of phenomena considered in the application of quantum theory. ” At that time, Bohr mockingly said: “Even if Einstein sent me a radiogram with the message that he now owns the ultimate proof of the reality of light particles, even then this radiogram would be able to reach me only with the help of electromagnetic waves, of which the radiation consists.”

Later, however, Einstein’s hypothesis about light quanta began to be regarded as one of his most important achievements. For example, in 1937, C. Compton (brother of the famous Arthur Compton) wrote that the light quanta hypothesis is “a contribution to physical theory, of course, comparable in importance to its more impressive and more widely known general theory of relativity, but which gave many more useful applications ".

A detailed experimental test of the Einstein equation for the photoelectric effect was performed in 1914-1916 by the American physicist Robert Milliken (R. Millikan, 1868-1953). Subsequently, Milliken wrote: “I spent 10 years of my life testing this Einstein equation of 1905, and contrary to all my expectations I had to unconditionally admit in 1915 that it was experimentally confirmed, despite its absurdity, since it seemed to contradict everything that we know about the interference of light. " This again suggests that at that time many physicists considered Einstein’s hypothesis to be almost a crazy idea.

Einstein also applied Planck’s quantum ideas to the calculation of the molecular heat capacity. As early as 1819, French physicists Pierre Dulong (PL Dulong, 1785-1838) and Alexis Petit (A.T. Petit, 1791-1820) experimentally discovered the law bearing their name. It reads as follows: the amount of heat required for the temperature of one gram molecule of any element in the solid state to increase by 1C "is about 6 calories. Then deviations from this law were detected at low temperatures and in the case of very solid crystals, for example , diamond. These deviations could not be explained for a long time. The explanation of the Dulong and Petit law was based on the classical theorem on the uniform distribution of energy over degrees of freedom. But according to Planck as applied to radiation, this theorem is not It is efficient throughout the frequency range. In his 1907 work, Planck’s Radiation Theory and Specific Heat Capacity Theory (Collection of scientific papers, M .: Nauka, Vol. III, 1966, p. 134) Einstein used Planck’s idea and suggested that quantization this is a common property of collective motion ***. Then, like electromagnetic radiation in a vacuum, the ripples of atoms (and ions) in crystals, according to Einstein's idea, should also be quantized. Einstein wrote: “... Until now believed that the movement of molecules is subject to the same laws, which obeys the movement of our bodies everywhere ... experience-today, now we have to make the assumption that for oscillating at a certain frequency of the ions involved in the exchange of energy between matter and radiation, a set of states that can take these ions is less than for the bodies of everyday experience. At the same time, we must assume the mechanism of energy transfer such that the energy of the elementary formation can take only the value 0, hv, 2hv, and so on. ” He established that if there is a cola in a crystal with a frequency such that the corresponding quantum of energy hv far exceeds the thermal excitation energy, then at a given temperature such colony cannot be excited. Thermal motion will not be distributed over all crystal crystal lines, but only over their low-frequency part. In this area, each colony receives as much energy as is supposed by the theorem on the uniform distribution of energy, and the entire crystal, as a whole, receives less energy. This explains the deviations from the law of Dulong and Petit. Later on, the theory of the heat capacity of solids was perfected by Peter Debye (P.Debye, 1884–1966), Max Born (M. Born, 1882–1970), and Theodor Karman (T. Kagtap, 1881–1969). This theory was brilliantly confirmed in experiments.

Einstein used the hypothesis of light quanta in 1916 to study the equilibrium between a gas of molecules and radiation (Collection of scientific papers, M .: Nauka, Vol. III, 1966, pp. 386, 393). He first introduced probabilistic concepts in the theory of radiation of atoms and molecules using Einstein coefficients.

Let us consider two any states of an atom with energies Ет and Е „(at Ет> Еп) (fig. 2.2). The probability of a spontaneous transition in

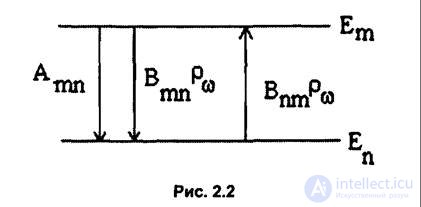
a unit of time Apt from state t to a state n. The quantity Apt has the meaning of the average number of