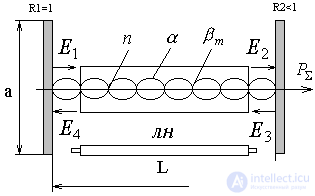
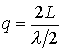
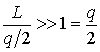
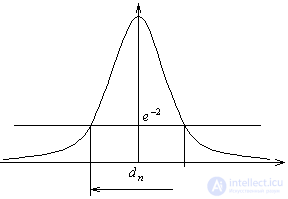
Due to the fact that the transverse dimensions are much larger than the length of the standing wave, the stationary field will have many types of colds *** that represent the stationary field distribution along the resonator and across. Their eigenvalues depend on the geometry and type of stationary function. The distributions along the resonator are called TEM mng longitudinal mode. Each mode has its own frequency. This uneven distribution of the field in the far-field Fresnel gives the radiation pattern the appearance of pants. In the practice of using lasers they try to use the single-mode mode.
As you know the conditions of the excitation of the oscillator:
1) PIC availability 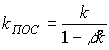
2) Depth of communication 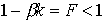
Critical case when 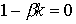 i.e.
i.e. 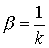 .
.
The laser resonator consists of two mirrors R 1 , R 2 form the usual collar *** circuit, which performs the selection in frequency and phase.
The smaller the size and the mirror the smaller the angle
1) Rays beyond the resonator carry energy and introduce additional diffraction losses.
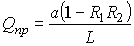
2) Energy is accumulated in the cavity due to the interference of the forward and reverse waves.
3) The task of the resonator to form the spatial distribution of the field.
The resonator is characterized by good quality:
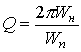
The larger the size of the resonator, the greater its quality factor due to the increase in energy.
The number of addition of waves in the resonator:
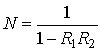
This is an indicator of how many times the wave interferes in the resonator until the amplitude decreases in 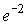 time.
time.
Losses in the laser, reducing the quality factor:
1) Leaky laser. Radiation loss coefficient
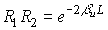
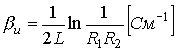
2) Absorption loss in the material:
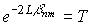
3) Loss of dispersion in the material:
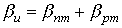
4) Losses at the ends of the active elements:
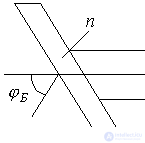
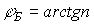
5) Absorption loss in the mirror:
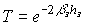 ,
, 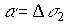
Full phase shift:
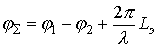
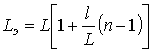 ,
, 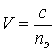 ,
, 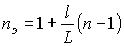
Set the conditions for self-excitation of the laser, for which we use the design scheme:
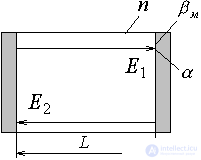
We write the field equation after the passage of a wave in the resonator:
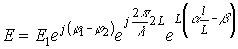 (one)
(one)
If completely filled, then 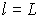
1) Phase condition of self-excitation:
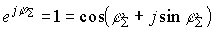
2) Amplitude balance:
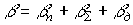
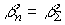
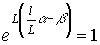
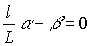
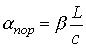 ,
, 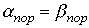
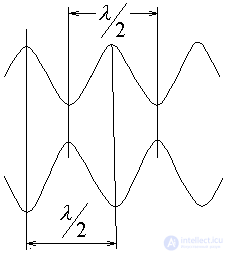
From equation (1) it follows that is a periodic function. In this case, equation (1) is performed for: 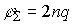 ;
; 
Note: with phase balance, we consider only waves traveling along the z axis.
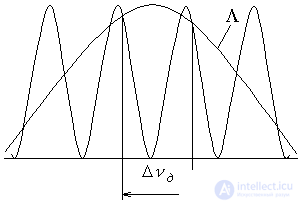
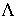 - Lorenz line, limiting the number of modes
- Lorenz line, limiting the number of modes
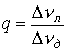
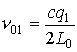 ,
,
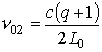
Electromagnetic energy accumulation:


Comments
To leave a comment
Quantum electronics
Terms: Quantum electronics