Lecture
Annotation: In this lecture, minimization methods are presented on the basis of the trial method, the Quine-MacClasky method, on the basis of minimizing diagrams for a function of 2, 3, 4 variables (Veitch diagrams).
Consider an arbitrary DNF. If you throw away any work in it, then the remaining expression will take a zero value on those sets as the original form, since  only then all the members
only then all the members  .
.
However, if the discarded product (implicant) was converted to one, and the function took a single value on this single set, then the remaining expression may no longer take a single value on this set. This means that the implicant was not redundant. If, by checking, it is established that the remaining expression turns into one, the implicant is redundant, and it can be discarded.
Example 1 :
Let it be given 
Drop the term x 1 x 2 :

x 1 x 2 = 1 => x 1 = 0, x 2 = 0

Because  then x 1 x 2 cannot be excluded
then x 1 x 2 cannot be excluded
Drop the term x 1 x 3 :

xone
x3
= 1 => xone
= 1, x3
= 1

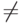 1 => x 1 x 3 cannot be excluded.
1 => x 1 x 3 cannot be excluded.

x 2 x 3 = 1 => x 2 = 0, x 3 = 1
 => x 2 x 3 - member extra.
=> x 2 x 3 - member extra.
If the verification shows that several implicants at the same time are superfluous, then they cannot be simultaneously excluded from the expression DNF. This can be done only alternately .
Example 2 :

 Those. the term x 1 x 3 x 4 cannot be excluded.
Those. the term x 1 x 3 x 4 cannot be excluded.
 Those. member x 2 x 3 x 4 is superfluous.
Those. member x 2 x 3 x 4 is superfluous.
 Those. member x 1 x 2 x 4 is superfluous.
Those. member x 1 x 2 x 4 is superfluous.
 I.e. member x 1 x 2 x 3 is superfluous.
I.e. member x 1 x 2 x 3 is superfluous.
 I.e. The term x 2 x 3 x 4 is not superfluous.
I.e. The term x 2 x 3 x 4 is not superfluous.
Exclude at the same time members 2, 3, 4

Let us check the values of f simultaneously on those sets in which all the dropped members turn into one.




those. it is evident that in the totality of this can not be done
Eliminate the term x 2 x 3 x 4 , we get:

Let us check if those terms in the expression are superfluous members that turned out to be superfluous in the original expression, i.e.: x 1 x 2 x 4 and x 1 x 2 x 3 .
x 1 = 1; x 2 = 0; x 4 = 1
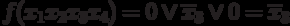 those. member x 1 x 2 x 4 is not superfluous
those. member x 1 x 2 x 4 is not superfluous
x 1 = 1; x 2 = x 3 = 0
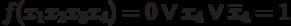 i.e. member x 1 x 2 x 3 is superfluous,
i.e. member x 1 x 2 x 3 is superfluous,
therefore  - deadlock form.
- deadlock form.
Checking then, starting with the exclusion of the third member, we obtain another dead-end form. Then choose the minimum of them.
The disadvantage of the method lies in the fact that with a large number of members it becomes cumbersome, because it is associated with the enumeration of various options. The machine implementation of this method is therefore complex. When automating the search for minimal forms, the method is practically not used.
The main disadvantage of Quine's method is that when searching for simple implicants it is necessary to make pair-wise comparisons at the beginning of all the constituent units, then obtained as a result of gluing the works.
In order to simplify this procedure, Mac-Klasky proposed an algorithm whose essence boils down to the following:
Example :
The product x 1 x 2 x 4 for a function depending on five variables must be assigned to the following numeric set: x 1 x 2 x 4 : 11-0-
We present a graphic representation of the simple implicant search process for the function presented in the following SDNF:

we write the expression of the function in the form of a disjunction of digital equivalents:

In the graphic method of finding simple implicants, at first all digital sets are divided into groups and these groups are arranged in the following order: first there is a group of digital equivalents containing only zeros (there can be one such set), then a group with sets containing one unit, then two and so on By comparing sets of neighboring groups, the possibility of gluing is established, the necessary mark is made and the result of gluing is written. The process continues until glueing is possible. All non-glued sets, as well as the final results of gluing, give simple implicants. Decoding received digital equivalents is obvious.
For our example, it looks like this:
| Digital equivalents are constituents of a unit | Gluing marks | Gluing result | Gluing marks |
|---|---|---|---|
| 1000 | * | 10-0 | - |
| 0101 | * | ||
| 1010 | * | -101 | - |
| 1101 | * |
So, simple implicants:
10-0 and -101, i.e. 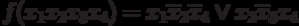
To search for the minimal form of a function, the method of implicant matrices is used. The essence of the method is as follows: an implicant matrix is composed, the columns of which are referred to as the constituents of the unit, and the rows - as simple implicants. Then there is a minimal coverage of all constituents of the unit with the simplest implicants. At the same time, such a minimal set of simple implicants is searched for, which together cover all the constituents of the unit of the original function. The fact of coverage is marked in the matrix cell by the symbol * (asterisk) in the case when the implicant covers the corresponding constituent (is its own part). Of all the simple implicants, only those that select only the constituents of the unit (in the matrix column only one symbol of coverage) are selected first, then the search is performed.
Example :
| Simple implicants | Constituent units | |||||
|---|---|---|---|---|---|---|
| A | B | C | D | E | F | |
| r | * | * | * | |||
| p | * | * | * | |||
| q | * | * | ||||
| m | * | |||||
| n | * | * | ||||
It is clear from the matrix that implicants n (covers the constituent F), implicant r (covers the constituent D) will necessarily enter the minimal form of the function. The same is true of implicants p. As for the rest, you need to choose the minimum set.
So:

Those. This function has two equally minimal forms.
Note : an important circumstance complicating the minimization of functions is the presence of enumeration of various options when searching for optimal coverage.
This method of graphic minimization was outlined by Carnot, who introduced special cards. These cards allow for a function that depends on a small number of arguments (up to five to six) to find the results of all possible gluing. Maps were subsequently improved by Weitch, and the method itself is sometimes referred to as the minimization method using Weitch diagrams.
Consider the essence of the method for functions depending on 2, 3 and 4 variables.
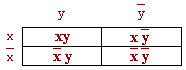
A diagram is a matrix whose columns and rows are assigned the meaning of variables entering the function in direct or inverse form.
In the cells of the matrix put the product, formed from the letters, which are called the rows and columns of the matrix.
We draw attention to the fact that this matrix immediately indicates a possible gluing of products that are included in the expression of the function.
So all the works, located in the adjacent vertical and horizontal cells, are subject to gluing together.
Moreover, the same diagram gives the result of gluing: it is the name of either a row or a column. When minimizing by this method, the function diagram of 2 variables is filled in according to the following rule: if a product enters the PDNF function, then a unit is put in the corresponding cell of the diagram, and zero - otherwise. If there are at least two adjacent units in the diagram, this means that the two works are glued together, and the result of gluing is the product (in this case, of one letter), the name of which is the given row or column.
Example :

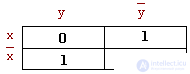
Select neighboring units in the diagram, and the result of gluing gives the minimum form of the function: 
Note that the result of gluing is the result of covering the constituents of the original function with simple implicants. In this case, the variables that named the rows and columns of the chart.
To minimize the functions depending on the three variables, the following diagram is used:
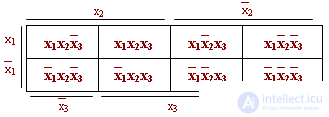
From the diagram it is clear that all works located in adjacent cells, as well as in cells located at the edges of the diagram, are subject to gluing together. The result of gluing is a piece containing one letter less. It is also seen that further gluing is possible, however, already between works located in a mutually perpendicular direction.
Consider, for example, the left half of the diagram:
| x 1 x 2 x 3 | x 1 x 2 x 3 |
| x 1 x 2 x 3 | x 1 x 2 x 3 |
We glue in pairs the works in rows:
| x 1 x 2 | x 1 x 2 |
| x 1 x 2 | x 1 x 2 |
Now we see that it is possible to make further gluing together, but works in the columns of the matrix:
| x 2 | x 2 |
| x 2 | x 2 |
As you can see, the result of gluing is the product x 2 . It is this variable that covers all four constituents of the unit of the PDNF function.
A similar statement is true for the constituents located in the rows and columns of the diagram along the edges of the table.
Thus, when searching for the minimum form, it is necessary to consider the left edge of the table glued to the right. It is said that, for clarity, it is possible to conditionally present this diagram as applied to the surface of a cylinder.
Example :

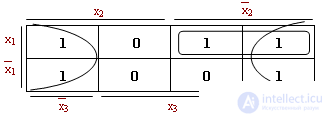

We see that two units corresponding to the constituents x 1 x 2 x 3 and x 1 x 2 x 3 are covered by the product x 1 x 2 .
For functions of 4 variables, the following diagrams are used:
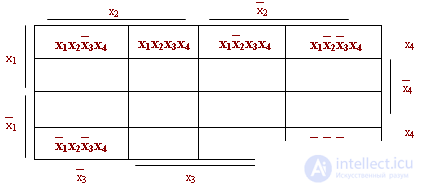
Everything that has been said about functions of 2, 3 variables is also true in this case. But this diagram has an additional feature: when searching for the minimal form of a function, it is necessary to consider the right edge with the left and the top with the bottom edge glued together.
It is said that for convenience it is advisable to consider this diagram written on the surface of the torus.
Example :
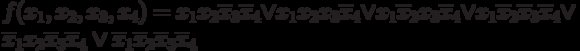
Make a diagram:

Note that based on the property of the diagram, four units standing in the corner cells of the diagram correspond to the constituents that are glued together.
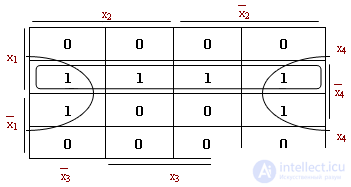
So, we give a formalized description of the method.
DefinitionThe correct configuration of the rank K is the set of ones (zeros), forming a rectangle with an area of 2 k .
To minimize the function depending on n arguments, the correct configurations are searched for, first n-1 rank, then n-2 rank, etc.
Next, the covering of the found correct configurations is determined by the joint projection of the corresponding rows and columns, which highlights the given correct configuration.
C - the correct configuration
A, B, D - configuration projections
A * B - the result of gluing
With the help of the Veitch diagrams one can find:
Let f (x 1 x 2 x 3 ) be defined not in the form of the SDNF, but in the DNF:

Fill in the appropriate chart:
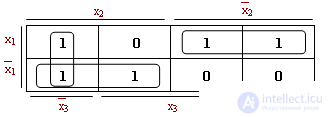
Because  , the units are placed in the corresponding cells of the diagram.
, the units are placed in the corresponding cells of the diagram.
Therefore: 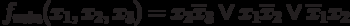
The advantage of the method: simplicity and clarity for a small number of arguments.
Disadvantages: the inapplicability of the method for a large number of arguments (> 6) due to the complexity of the diagrams and loss of visibility.
Comments
To leave a comment
Digital devices. Microprocessors and microcontrollers. computer operating principles
Terms: Digital devices. Microprocessors and microcontrollers. computer operating principles