Lecture
The lecture gives the concept of Boolean algebra, describes the problems of analysis and synthesis. The description of elementary functions of one and two variables is given. Basic equivalences are presented.
In addition to the usual algebra, there is a special one, the foundations of which were laid by the nineteenth century English mathematician J. Boole. This algebra deals with the so-called propositional calculus.
Its peculiarity is the applicability for describing the operation of so-called discrete devices, among which belong a whole class of automation devices and computing equipment.
In this case, the algebra itself acts as a model of the device. This means that the operation of an arbitrary device of the specified type can only be described in some respects using the constructions of this algebra. A real real device does not physically work as the algebra of logic describes it. However, the application of the provisions of this theory allows us to make a number of practical generalizations.
Consider some scheme and present it in the form of a so-called "black" box.
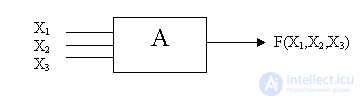
We assume that the internal contents of the box is unknown.
X 1 , X 2 , X 3 - input signals, F - output signal.
We also consider that the scheme A is elementary, i.e. there is no other scheme B less than A that would be contained in A.
We construct an abstract device from elementary devices, such as A, B, C, etc. Obviously, a more complex device can be constructed from simple ways:
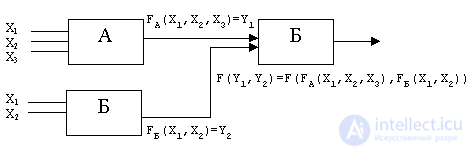
Then the role of Y 1 for the second element B will play:
Y1=FА(X1,X2,X3) Y2=FБ(X1,X2) F=F(Y1,Y2)=F(FА(X1,X2,X3),FБ(X1,X2))
Parallel connection of elements does not change the function, therefore, from the point of view of logic, this type of connection is not used. Physically sometimes they still use a parallel connection of elements, but mainly in order, for example, to amplify a signal.
In this regard, the parallel connection of elements in the algebra of logic is not considered.
The function that the element performs, generally speaking, depends on the variables that are fed to the input.
Therefore, the rearrangement of the arguments affects the nature of the function.
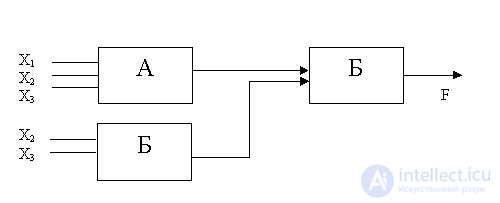
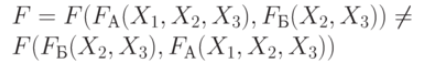
Thus, arbitrary, arbitrarily complex in a logical sense, schemes can be built using two methods:
These two physical techniques in the algebra of logic correspond:
So, the physical task of building and analyzing the work of a complex device is replaced by the mathematical task of synthesis and analysis of the corresponding functions of the algebra of logic.
There are several synonyms in relation to the functions of the algebra of logic:
As required, we will use all these synonyms.
Consider some set of arguments:
and we will assume that each of the arguments takes only one of two possible values, independently of the others
What is the number of different sets?
Let each binary set correspond to some binary number:
It is obvious that the number of different X 1 , X 2 , ........... X n n-digit numbers in a positional binary system is 2 n .
Suppose that a certain function F (X 1 , X 2 , ... X n ) is given on these sets and on each of them it takes either the '0' th or '1' th value.
Such a function is called a function of the algebra of logic or a switching function.
What is the number of different switching functions of the 'n' arguments?
Because the function on each set can take the value '0' or '1', and the total number of different sets is 2 n , then the total number of different functions of the arguments 'n' is: 2 ^ 2n.
Compared to the analytic function of a continuous argument, even for one argument there are many different functions.
| Number of arguments | one | 2 | 3 | four | five | ten |
|---|---|---|---|---|---|---|
| The number of different switches. f-tion | four | sixteen | 256 | 65536 | ~ 4 * 10 9 | ~ 10 300 |
Different computer devices contain tens and hundreds of variables (arguments), so it is clear that the number of different devices that differ from each other is almost infinite.
So, you need to learn how to build these complex functions (and therefore, the device), as well as analyze them.
| The task of synthesizing more complex functions is to represent them through simple, on the basis of operations of superposition and substitution of arguments. |
Thus, it is first necessary to study these elementary functions in order to build more complex ones on their basis.
FAL of one argument
To set the PLL, you need to set its values on all sets of arguments.
| Argument x | value | Function name | |
|---|---|---|---|
| 0 | one | ||
| F 0 (x) | 0 | 0 | constant '0' |
| F 1 (x) | 0 | one | variable 'x' |
| F 2 (x) | one | 0 | inversion of 'x' (negation of x) |
| F 3 (x) | one | one | constant '1' |
Let the function set an index equivalent to the set of its values for the corresponding values of the argument, starting from 0.0, ...., n, ....., etc. in ascending order.
These functions can be implemented on 4 elements, each of which has a maximum of one input. Thus, the principle of substitution of arguments for constructing more complex functions cannot be used.
It is necessary to consider more complex functions, i.e. FAL 2 arguments.
We give these definitions:
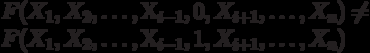
Otherwise, it does not depend significantly, and the corresponding argument is called fictitious.
For example:
| X 1 | X 2 | X 3 | F (X 1 , X 2 , X 3 ) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | one | 0 |
| 0 | one | 0 | one |
| 0 | one | one | one |
| one | 0 | 0 | 0 |
| one | 0 | one | 0 |
| one | one | 0 | one |
| one | one | one | one |
It can be seen that X 3 is a dummy argument. This shows that in the function you can enter any number of dummy arguments, on which it does not significantly depend. This technique will be needed later to perform a number of transformations.
All FAL from 2 arguments. We reduce them into a single table 2.1.
| Function number | The value of the function on sets of logical variables | Function name | Function designation | |||
|---|---|---|---|---|---|---|
| X 1 | 0 | 0 | one | one | ||
| X 2 | 0 | one | 0 | one | ||
| f 0 (X 1 , X 2 ) | 0 | 0 | 0 | 0 | Constant "zero" |
f (xone X2 ) = 0 |
| f 1 (X 1 , X 2 ) | 0 | 0 | 0 | one | Conjunction |
|
| f 2 (X 1 , X 2 ) | 0 | 0 | one | 0 | Ban on X 2 |
|
| f 3 (X 1 , X 2 ) | 0 | 0 | one | one | Variable x 1 |
f (xone X2 ) = Xone |
| f 4 (X 1 , X 2 ) | 0 | one | 0 | 0 | Ban on X 1 |
|
| f 5 (X 1 , X 2 ) | 0 | one | 0 | one | Variable x 2 |
f (xone X2 ) = X2 |
| f 6 (X 1 , X 2 ) | 0 | one | one | 0 | Addition mod2 (disparity) |
|
| f 7 (X 1 , X 2 ) | 0 | one | one | one | Disjunction |
|
| f 8 (X 1 , X 2 ) | one | 0 | 0 | 0 | Pierce arrow |
|
| f 9 (X 1 , X 2 ) | one | 0 | 0 | one | Equivalence |
|
| f 10 (X 1 , X 2 ) | one | 0 | one | 0 | Inversion X 2 |
f (xone X2 ) = ^ X2 f (xone X2 ) = X2 |
| f 11 (X 1 , X 2 ) | one | 0 | one | one | Implication from X 2 to X 1 |
f (xone X2 ) = X2 -> Xone |
| f 12 (X 1 , X 2 ) | one | one | 0 | 0 | Inversion X 1 |
f (xone X2 ) = ^ Xone f (xone X2 ) = Xone |
| f 13 (X 1 , X 2 ) | one | one | 0 | one | Implication from X 1 to X 2 |
f (xone X2 ) = Xone -> X2 |
| f 14 (X 1 , X 2 ) | one | one | one | 0 | Schaeffer Barcode |
f (xone X2 ) = Xone | X2 |
| f 15 (X 1 , X 2 ) | one | one | one | one | Constant "one" |
f (xone X2 ) = 1 |
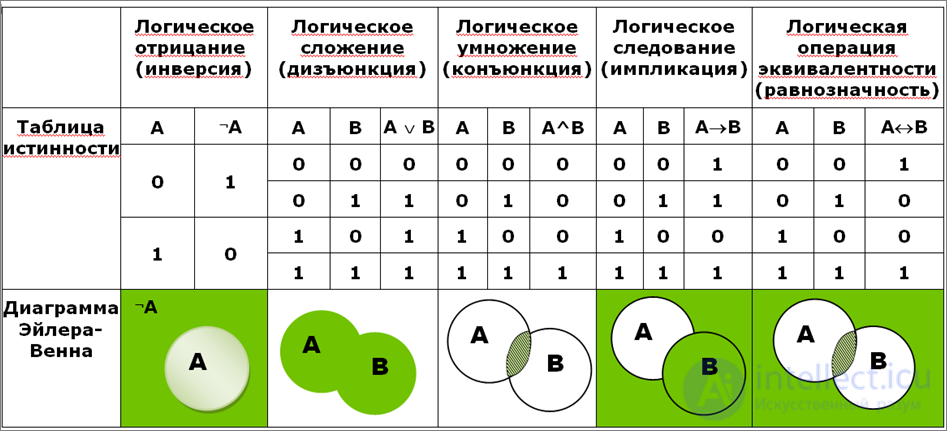
These functions are introduced formally. However, they can be given a certain "logical" meaning. The algebra of logic is often called propositional calculus.
At the same time, a statement is understood as any sentence in relation to which it can be argued that it is true or false.
For example:
B =
there is a true saying.
Let us consider what semantic content can be put into some complex statements using the example of the PUL of 2 arguments.
Inversion
Read NOT X or X with a dash, negative X.
Take, for example, the following statement: A = , then the complex statement NOT A means: it is not true that A, i.e. it is not true that the .
From simple statements one can construct more complex ones using so-called connections.
Logical connections are FALs whose arguments are simple sentences.
Conjunction
Take 2 statements:
A = B =
then a complex statement: A & B will be true, since both of these statements are true.
Since the truth table for conjunction coincides with the multiplication table, if the true statement is assigned the value '1' and the false statement is assigned the value '0', then a complex statement can be called a product.
| X 1 | X 2 | f 1 (X 1 , X 2 ) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | one | 0 |
| one | 0 | 0 |
| one | one | one |
The conjunction function is true when both statements are true at the same time.
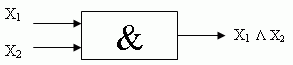
Disjunction
This complex statement is true when at least one statement included in it is true.
| X 1 | X 2 | f 1 (X 1 , X 2 ) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | one | one |
| one | 0 | one |
| one | one | one |
X 1 OR X 2 is read: Some difference from the meaning of the union "or", adopted in Russian: in this case, this union is used in the sense of unification, not separation.

Logical equivalence
This complex statement is true when both statements are true or false at the same time.
It follows that, regardless of the meaning, both true and false statements are equivalent.
For example,
A = B = A ~ B are equivalent.
Implication
This complex statement is false only when X 1 is true and X 2 is false.
| X 1 | X 2 | f 1 (X 1 , X 2 ) |
|---|---|---|
| 0 | 0 | one |
| 0 | one | one |
| one | 0 | 0 |
| one | one | one |
It reads: if X 1 , then X 2 . At the same time, X 1 is a premise, X 2 is a consequence.
If you look at the truth table, then the name of this function may seem strange, since it follows that a statement made up of two false may be true.
But in reality, that's right, because the content of statements in the algebra of logic is not interested.
Then a false consequence can follow from a false premise and this can be considered true:
, then <2 square 3>.
Equivalence
In some cases, a complex and long utterance can be written shorter and simpler without violating the truth of the original utterance. This can be done using some equivalent ratios.
Disjunction:

those. the truth of a statement does not change if it is replaced by a shorter one, so this is the rule for bringing such members into account:
xvx = 1

- constantly true statement.


- (commutative) communicative law.

- a combination law.
Conjunction:

rule of bringing such members:

 - constantly false statement
- constantly false statement
 - constantly false statement
- constantly false statement
Addition mod 2
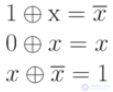
 - with an odd number of members, 0 - with an even number of members
- with an odd number of members, 0 - with an even number of members
Rule de Morgan
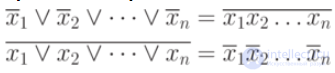
Let us prove for two variables using the truth table:
| X 1 | X 2 |  |
X 1 & X 2 |
|---|---|---|---|
| 0 | 0 | one | one |
| 0 | one | one | one |
| one | 0 | one | one |
| one | one | 0 | 0 |
Absorption operation:
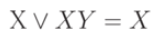 or in general
or in general 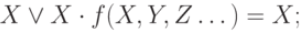
Full bonding operation:
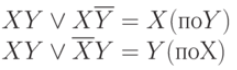
Incomplete bonding operation:
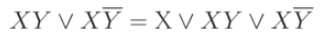
Comments
To leave a comment
Digital devices. Microprocessors and microcontrollers. computer operating principles
Terms: Digital devices. Microprocessors and microcontrollers. computer operating principles