8.Modified additional and reverse codes.

The lecture describes the modified additional and reverse codes. Given methods for multiplying fixed-point numbers in direct and additional codes, as well as shift algorithms

An important feature of the considered codes is that in the process of performing the operation of addition and subtraction there is no overflow of the digital part of the number and transfer to the sign bit. Overflow occurs only in a significant discharge. This happens because the sum of the two terms in absolute value is less than one.

When solving real-life problems, it is often difficult to determine in advance whether the sum of two terms is less than one. In any case, to prevent overflow, you can impose additional restrictions on the value of the terms, narrowing the range of numbers with which the machine operates. Both are unacceptable.

Consider this example:

That is, we get the wrong result both in sign and in the digital part.

Consider another example:

That is, in this case the overflow in the digital part distorts the result of the operation.

It can be noted that the overflow of the numerical grid occurs in the case of identical terms of the terms, since it is in this case that the result module exceeds the modules of each of the terms, the fact of overflow itself can be fixed by changing the sign of the result.

Thus, one of the ways to fix an overflow is to automatically determine the transition from the same signs of the terms to the opposite sign of the result.

However, this method of fixing overflow is inconvenient, since the prefixed characters of the addends must be remembered, compared to each other and after receiving the result.

There is another principle of overflow fixation. This principle is based on the use of so-called modified codes. It is obvious that in case of overflow of the discharge grid, calculations must be stopped or, at least, a special sign of overflow is generated, and the decision to stop the calculations lies with the programmer.

The essence of the modified codes is that one more digit is added to the sign bit:

"+" is assigned to 00

"-" is set to match 11

Then, by definition, a modified additional number code is called

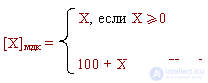
The transfer arising in sign discharges is lost. In general, the modified code does not differ from the simple additional one. Similarly, by definition, the reverse code is:

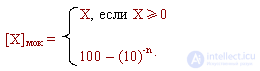
As in the case of a simple reverse code, the resulting transfer unit in sign bits along the cyclic transfer chain is added to the low order digit of the number.

Since only numbers less than one still participate in addition,

  S = X + Y <2 

Therefore, the most significant digit cannot be distorted by the transfer from the digital part of the number, on the other hand, the transfer that occurs when adding numbers in the case when

  S = X + Y> 1 

distorts the lower order digit.

The inconsistency of the sign bits after the operation indicates that there is an overflow.

There are two types of overflow:

• "01" - positive
• "10" is negative.

The first is assigned a combination of 01 in significant digits, and the second - 10.

Examples

Modified Additional Code:

Modified Reverse Code

Multiplication of high order numbers in direct code

This is the analytical record of the algorithm for multiplying two numbers, starting with the higher digits of the multiplier.

Algorithm:

• Multiply shifts to the right by 1 bit
• The multiplier figure is analyzed. If it is zero, then the partial product is not cumulative, and if it is one, then the partial product is added to the total result.
• The sequence of operations in paragraphs 1 and 2 continues "n" times.

• The mark of the work is located independently of the receipt of the digital part according to the formula:

  

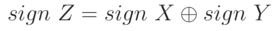
Example:

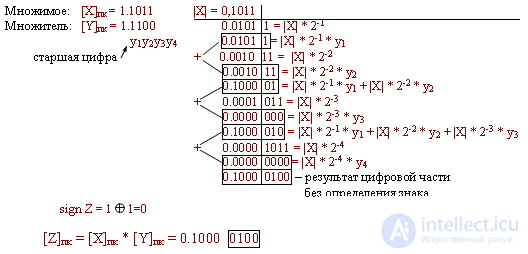
It can be seen that in the general case it is necessary to have for an accurate result a grid with the number of digits equal to the sum of the digits of the multipliers.

If you want to get the product with an accuracy not worse than 2 -n , then it is enough to have not doubled the size of the discharge grid, but only increased by

   digits 

Multiplication with lower order bits in direct code

We write an expression for the product of two numbers in a slightly modified form, namely:

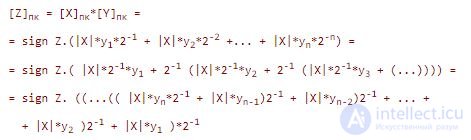
This expression is called the Horner transform and sets the multiplication algorithm with the lower digits of the multiplier.

Thus, for multiplication, the following sequence of actions should be performed:

• The least significant digit of the multiplier is analyzed. If it is equal to "1", then the multiplicand is involved in the formation of part of the work. Otherwise - not involved.
• The resulting partial product is shifted to the right by 1 digit.
• Operations on items 1 and 2 are performed until the senior level.

Example:

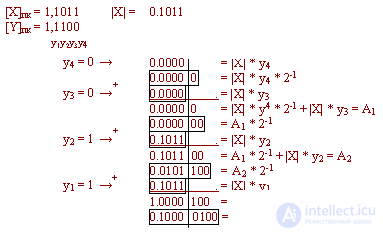
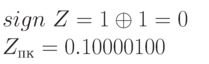
Comment.

To produce a work with an accuracy not lower than 2 -n, you only need to have an "n" - bit grid.

So, we see that in order to obtain a product, both when multiplying from higher and lower digits, it is necessary to perform two microscopic operations: summation of numbers in a positional number and shift system.

However, it is known that numbers can be represented in different codes (these are, first of all, negative numbers).

We already know how the operation of summation of numbers (including with different signs).

However, the micro-shift operation has some features:

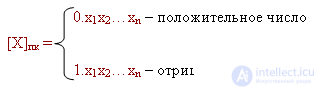
Shift right:

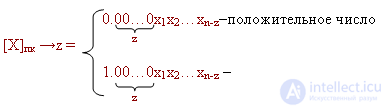
Shifting to the left is possible only if the shifted number is less than one modulo one:

Initial numbers:

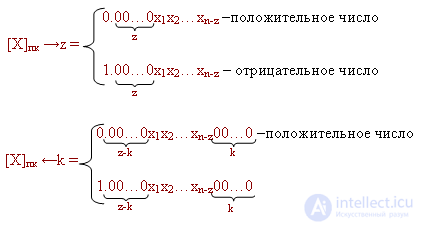
If it is purely formal to make the conversion of the expression of a certain number written in the direct code before performing the shift and after the micro shift operation, into the reverse modified code , then:

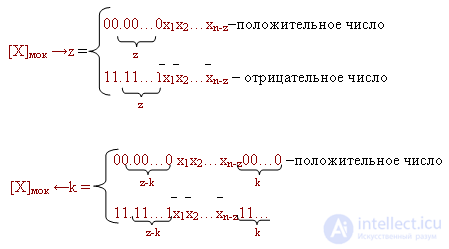
That is, when a negative number is shifted to the right, the upper digits are filled with units. At shift to the left units are written to the senior and junior categories.

Using similar rules, it is easy to establish that when shifting to the left a negative number in the modified additional code, the lower digits of the shifted number must be filled with zeros.

Multiplication with lower digits in the additional code

If y n = y n + 1 , then the partial product is shifted.

If y n = 0 and y n + 1 = 1, then [X] dk is added to the partial product

If y n = 1 and y n + 1 = 0, then [X] dk is subtracted from the partial product.

Example:

Multiplication with higher digits in the additional code