3: Perfect disjunctive and conjunctive normal PAL forms

Annotation: The lecture provides a definition of perfect disjunctive and conjunctive normal forms. Presents the rules for recording functions by zero and one. The concept of functional completeness is given, the task of minimizing the function is posed. Quine's theorem is formulated.

We introduce the concept of degree:

Consider the conjunction of the form:

There are 2 ⁿ sets of view Let us assign the number of the set i to the correspondence of each conjunction (*) and form the disjunction of all the conjunctions:

Theorem (without proof) :

Any FAL depending on the 'n' arguments can be represented in the form:

This theorem implies a number of important consequences:

1. It provides an opportunity to move from the table assignment of the function to the analytical form and make the reverse transition.
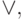
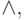2. Sets the so-called functional completeness of the ligaments (basis) " - "because it will allow to build in this basis an arbitrary PLL of an arbitrary number of arguments.

Note :

1. If a then the corresponding form of the function is called disjunctive normal (DNF).
2. If i = n, then the canonical form of the function is called perfect DNF (CDNF). Disjunctions are taken over those sets on which the function f (X_ {1}, X_ {2}, ..., X_ {n}) = 1

Example: DNF

Example: PDNF

In a DNF, every variable contains any variable in direct or negative form.

The analogous theorem is also valid for the representation of a function in conjunctive normal form (CNF):

or when presented in perfect CNF (SKNF):

where: & means that conjunctions are taken according to the sets on which

  f (X_ {1}, X_ {2}, ... X_ {n}) = 0. 

Based on these theorems, we give the rule for the transition from the tabular form of a function to SDNF and SKNF.

The transition from the tabular form of the function to the PDNF or the rule for writing the function by units:

1. Select those sets of arguments on which f (X_ {1}, X_ {2}, ... X_ {n}) = 1.
2. Write all conjunctions for these sets. If at the same time X_ {i} has the value '1', then this multiplier is written directly, if '0', then with negation.
3. All conjunctive members are joined by disjunction

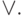
Example :

The rule of transition from the table form of the function assignment to the SKNF or the rule of writing the function by zeros .

1. Select those sets of arguments on which f (X_ {1}, X_ {2}, ... X_ {n}) = 0.
2. If at the same time X_ {i} has the value '0', then it remains unchanged. If '1', then with negation.
3. All disjunctive members are joined by a conjunction sign.

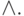
Example :

Example :

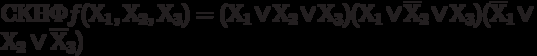
Consider the method of obtaining SDNF from SKNF and back.

From table 2.1, using the method of writing a function by zeros, it follows that the SKNF of the same function of disjunction will look like:

So, we have two forms of the same function:

So, it is clear that the total number of members in these two forms is equal to the sum of the zeros and units of the function, that is, it is equal to 2 ⁿ .

If the original form of the function written in the SKNF or SDNF contains z members, then in its other form (that is, the CDNF or SKNF) they will be (2 ⁿ - z).

Since we include disjunctive or conjunctive terms in the function and take them according to the sets on which the function either turns into '0' or '1', in order to switch from one form of setting the function to another, you need to write out all the missing members and put them over each variable negation, and also replace conjunction signs with disjunction and back.

those. Received PDNF.

The practical meaning of the transition is that it is possible to determine the implementation of which form will require a smaller amount of equipment.

The concept of functional completeness FAL

It was noted that the technical (physical) problem of synthesizing an arbitrary device is reduced to the mathematical problem of constructing an arbitrary PAL.

The question naturally arises: how many bundles are needed to build an arbitrary PLL. The answer to this question is not straightforward. We see that, for example, using only the function f_ {0} (constant 0), f_ {15} (constant 1), an arbitrary PLL cannot be constructed. You can not build it with only an inverter. There are other bases: 1, |. There are also single element bases: f_ {8} is the Pierce arrow, f_ {14} is Sheffer's stroke, AND-NO, OR-NO.

Technically, the synthesis of a device means that you need to have a certain set of elements, the PLL of which form a basis so that you can build a real device.

However, as noted, the task of the synthesis of PAL is an ideal model. In fact, to build real devices use a slightly more expanded set of elements - amplification and correction of signals.

Minimization of FAL and limitations in its consideration

Let us show by example that SDNF is not an economical form of writing:

based on full gluing on X_ {2}, we see that the record has become shorter, because contains fewer bundles and letters. Physically, this means that a device that implements an equivalent, but simpler function will have a smaller amount of equipment, and therefore will work more reliably.

So, the task of device synthesis must be supplemented by the task of reducing the equipment in it. From a mathematical point of view, this is the task of building a minimum PLL.

Under the minimum FAL refers to this form, which contains a smaller number of letters and members than in its original form.

We are talking about letters, not variables, as in the function:

There are 6 letters and only 2 variables.

It can be seen that if any elementary product enters a function, then when new factors are added to it, the resulting product will also be included in the function.

Example : if X_ {1} X_ {2} enters into a function of any number of arguments (> 2), then it will include, for example, the product X_ {1} X_ {2} X_ {3}.

This can be shown as:

We give a number of definitions:

1. The product of one or several non-repeating variables, taken with or without negation, is called elementary.

   For example, X_ {1} X_ {2} X_ {3} is an elementary product, since it includes the various letters X_ {1} X_ {2} X_ {3}.
2. Disjunction of elementary products - DNF.
3. A DNF is minimal if it has a minimum number of letters and members.
4. The constituent unit of a function is a function that takes a unit value on only one set of arguments.

   Usually, the constituents of a unit are expressed through the product of all variables on which the function depends. SDNF - disjunction constitutional unit.
5. The rank of the work is the number of letters included in it.
6. The private part is the product obtained by dropping one or more variables.

   For example, X_ {1} X_ {2} X_ {3} X_ {4}, where X_ {1}, X_ {1} X_ {2}, X_ {1} X_ {2} X_ {3} are some proper parts .
7. If the function is zero on the sets of arguments on which the function F vanishes, then they say that is the implicant of the function F (that is, the zeros of the implicants are not less than those of the function).
8. A simple implicant is a work that itself enters into the expression of a function, but no its own part enters into the expression of a function.

   For example, : here X_ {1} is a simple implicant, and X_ {1} X_ {2} X_ {3} and X_ {1} X_ {3} are not simple.

Concept of coverage

Definition If on any set f takes the value a_ {1}, and - the value of a_ {2}, then it is said that f with its value_ {1} covers the value of a_ {2} of the function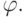

When minimizing FAL seek to get a form in which there will be fewer letters than in the original. In relation to DNF, this form is called abbreviated (Ju. DNF).

The meaning of building Juice. The DNF consists in the fact that it includes such elementary works that, with their units, cover not one unit of the original function, but several.

Thus, each elementary product included in the PDNF covers only one unit of the function.

For example :

  1 1 1 

These function units can be covered with shorter products: X_ {1} covers two units: and and which also covers two units: and i.e.

THEOREM (without a dock) :

Any FAL can only be represented in Juice. DNF, i.e. written in the form of a simple implicant disjunction .

A shortened form does not mean that this form is minimal. However, for practical implementation, this form is more convenient than perfect.

Consider the method of obtaining Juice. DNF proposed by Quine. This method, and, in particular, Quine's theorem explicitly and implicitly includes almost all minimization methods.

The original form of the function is perfect DNF.

Quine's theorem :

If in the PDNF at the beginning to perform all operations of incomplete gluing, and then all the operations of absorption, then the result will be a shortened DNF.

We show that by applying the operation of incomplete gluing, we obtain all simple implicants of the function. We introduce a deployment operation, which is the reverse of the gluing operation: this is the multiplication of each piece by the expression of the form

Let be - a simple implicant of some three variables. Then:

after repeated use of this operation, the constituents of the unit of the original function are obtained; her PDNF.

Generally speaking, this form may include several identical members, since different simple implicants can give the same constituent units. Therefore, rejecting the extra members in the DNF, we get its PDNF.

With respect to SDNF, the operation of incomplete gluing is used, since the same work, generally speaking, can be glued to several others, giving different implicants, so as not to lose the opportunity to carry out all the gluing operations, each work that participated in the gluing operation has to be left for other operations.

Example :

Thus, after performing the operation of incomplete gluing, you get not only the disjunction of a simple implicant, but also a part of the constitutional unit.

If we now carry out all the absorption operations, then in the resulting form of the function f only simple implicants will remain. Show it. Suppose, as a result of gluing operations, we get a member x that is not a simple implicant.

Then x = y * z, where z is a simple implicant, which should also be included in f, since it includes x. But z will absorb x, so x cannot enter f. This proves Quine's theorem.

Note : Note that Quine's theorem applies with respect to the SDNF function.

The procedure for obtaining juice. DNF may be as follows:

1. Perform all operations of incomplete gluing of the constituents of the unit of the original SDNF. The result is a product of (n-1) rank; the remaining non-glued constituents of the unit cannot participate in further gluing.
2. To cover all received works and the constituent unit. Some of the constituent units will be eliminated.
3. Continue until operations 1) and 2) are possible.

Example 1 :

If we apply the full bonding operation, we get:

or

or

those. we have no opportunity to further carry out the operation.

We now apply the incomplete bonding operation:

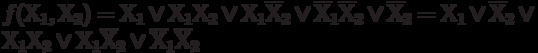
Simple implicants: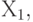

Constituent units:

Now we can carry out absorption operations:

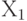absorb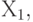s:

absorbs: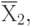

Those. abbreviated DNF

in this case, it is the minimal form.

Example 2 :

Let it be given:

Get the PDNF:

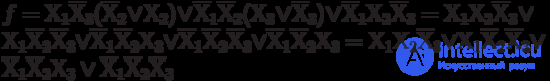
Now that you have PDNF, you can get abbreviated DNF:

Example 3 :

Two works are glued together, containing the number of variables with negation, differing by one and arranged accordingly.

Usually a piece containing 'n' letters is called a minter of a 'n' - rank.

The method of minimizing the FAL by Quine

Definition : A deadlock DNF is a disjunction of simple implicants, none of which can be excluded from the function expression.

This method of minimizing FAL is as follows:

1. Find a Juice. DNF.
2. Find all possible dead-end DNFs.
3. From the found TDNF choose the minimum.

Sometimes in Juice. DNF contains extra implicants. As already seen in the abbreviated DNF:

implicant \ overline X_ {2} X_ {3} can be excluded. Not one gluing and absorption operation can be applied to this form, since this is juice. DNF, i.e. disjunction of a simple implicant. You can use the deployment operation on X_ {1}:

Because X_ {1} X_ {3} covers X_ {1} \ overline X_ {2} X_ {3}

and \ overline X_ {1} \ overline X_ {2} covers \ overline X_ {1} \ overline X_ {2} X_ {3}, then

THEOREM :

Every minimal DNF is dead-end. The converse is not true. The proof is obvious.

This theorem implies an important corollary: In order to find the minimum DNF, you need to find all the dead-end forms and take the minimum among them.

There are several different ways to find dead-end forms.