9. methods of dividing numbers with a fixed comma in direct codes and additional (inverse) codes.

Abstract: The lecture gives methods for dividing numbers with a fixed comma in direct codes and additional (inverse) codes. Operations on floating-point numbers - multiplication, division, addition, subtraction are described.

The implementation of the division operation in a computer in a binary number system is simpler than in decimal. This is due to the fact that in determining each private number, only one sample must be made.

If the numbers X and Y are given in the direct code, and they are represented with a fixed comma, then two basic algorithms are used to perform the division:

• with shift and automatic balance recovery;
• with a divider shift and automatic recovery of the remainder.

Let: [X] _pk = sign X. x ₁ x ₂ ..x _n

[Y] _pc = sign Y. y ₁ y ₂ ..y _n

[Z] _pc = [X] _pc / [Y] _pc = sign Z. z ₁ z ₂ ..z _n

X and Y must be such that:

| Z | <1 (i.e. fixed comma )

Direct code division with shift and automatic restoring of the remainder

1. 
2. 

3. If a , then z ₀ = 1 and (z ₀ is the integer part of the result).

   If a then z ₀ = 0 and

etc.

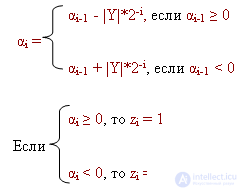
Example :

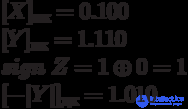
₊ 0.100 = [| X |] _dk

1.010 = [- | Y |] _dk

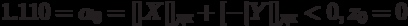
0.110 = [| Y |] _dk

1.010 = [- | Y |] _dk

0.110 = [| Y |] _dk

Answer: [Z] _pc = 1.101

Direct code division with divider shift and automatic remainder recovery

• 
• 

• If a then z ₀ = 1.

  If a then z ₀ = 0.

  

Bit grid (n + d) bits, where d = log ₂ n

Example :

  1) [X] 

  = 1.1001
 2) [Y] 

  = 1.1011
 n = 4, d = 2 

Answer: [Z] _pc = 0.1100

Example :

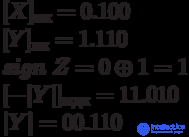
Answer: [Z] _pc = 1.101

Division in additional (reverse) codes with shift and automatic recovery of the remainder

[X] _{dk, ok} ; [Y] _{dk, ok}

The division in the OK does not apply, since the "0" in the OK has a double image. In the first measure instead of sign X is taken, and instead is taken [x] _{dk, ok}

Example :

  [X] 

  = 1.0111 
 [Y] 

  = 1.0011 
 Because  sign X = sign Y, then 

₊ 1.0111 | 1.0011

0.1101 = - [Y] _dk

______

1.0011 = [Y] _dk

______

0.1101 = + [- [Y] _dk ] _dk

______

1.0011 = [Y] _dk

______

0.1101 = + [- [Y] _dk ] _dk

______

Answer: [Z] _dk = 0.1011

This is true when 0 <= [Z] _dk = [X] _dk / [Y] _dk ] | <1.

If it is necessary to determine the quotient | [Z] _dk = [X] _dk / [Y] _dk | | <2, then do this:

[X] _dk * 2 ^-1 / [Y] _dk = z ₀ z ₁ z ₂ ... z _n , z ₀ is a sign, z ₁ is the integer part of a number.

Arithmetic operations on floating-point numbers

The basis of arithmetic operations on floating-point numbers are the principles on which operations on numbers fixed by a comma are based. At the same time there are some features.

We will conditionally assume that the orders are given in the reverse code, and the mantissas in the direct one.

Multiplication:

  X = 2 

  * sign Xx 

  x 

  ... x 

  Y = 2 

  * sign Yy 

  y 

  ... y 

  Z = X * Y = 2 

  * sign Zz 

  z 

  ... z 

The order of the operation is as follows:

1. The sign of the product is the same as when multiplying numbers with a fixed comma:
2. The order of the product is found by algebraic summation of the orders of the multiplicand and the multiplier.

3. The mantissa is found according to the rules for multiplying numbers with a fixed comma.

   The following cases are possible:

   • The mantissa of the work is an unnormalized number, since

     

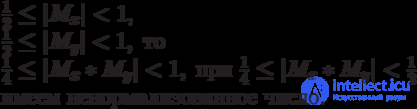
     Therefore, it is necessary to normalize to the left a maximum of only one digit .

     To this end, you need to move the mantissa to the left by one digit . This corresponds to multiplying a number by 2 ¹ . In order for the number not to double, you need to subtract one from the order.

   • When multiplying two numbers due to the limitedness of the discharge grid, you can get a number that cannot be represented in it. This corresponds to the receipt of machine infinity.

     In this case, a special feature is produced, according to which further calculations are terminated.

   • When multiplying two numbers, you can get the minimum number, which also can not be represented in the bit grid. This corresponds to the case when the resulting number should be interpreted as zero .

Division

Basically analogous to multiplication:

  X = 2 

  * sign Xx 

  x 

  ... x 

  Y = 2 

  * sign Yy 

  y 

  ... y 

  Z = X / Y = 2 

  * sign Zz 

  z 

  ... z 

The order of the operation is as follows:

1. By the well-known rules is the sign of the private
2. The order of the quotient is found as the difference between the orders of the dividend and the divisor.

3. Private figures are as follows:

   first is the whole part of the mantissa, i.e.

   If a , if a then z ₀ = 0.

The fractional part of the mantissa is the same as in fixed-point operations on numbers. This procedure follows from the fact that:

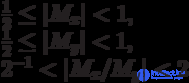
That is, it is possible to obtain a non-normalized mantissa. To normalize, the mantissa must be shifted to the right by one digit and, in order not to reduce the result by a factor of two, it is necessary to add one unit to the order.

When dividing, as well as when multiplying, it is possible to obtain a machine zero code and an infinity code.

Addition and subtraction

Both operations are performed using similar algorithms.

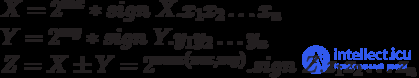
The operation is performed as follows:

1. The order difference is:
2. The alignment of the orders is made, while if the difference of orders is positive, then m _x is taken as the result order, and the mantissa M _y is shifted to the right by | m _x - m _y | discharges; If the order of digits is negative, then the mantissa M _{x is} normalized.
3. The algebraic summation of the mantis is made.
4. Normalization is performed left or right for the corresponding number of digits with the necessary order correction.

Example :

  mantissa order
 [m 

  ] 

  = 0.11 [M 

  ] 

  = 0.1010
 [m 

  ] 

  = 0.10 [M 

  ] 

  = 0.1110
 Find the order difference:
    

  00.11 = [m 

  ] 

  11.01 = [-m 

  ] 

  1 |  00.00
    | _ _-> 1

00.01 = - order difference.

  Since mx> m 

  , then:
        

  00.1010 = [M 

  ] 

  00.0111 = [M 

  ] 

  * 2 

  [Z] wet = 01.0001 - overflow
          2 

  * [Z] 

  = 00.1000 - normalization
                 max (m 

  m 

  ) = [m 

  ] 

  = 

  00.11
                               [one] 

  = 00.01
                              [m 

  ] 

  = 01.00 - order overflow

Z = .

When performing the addition operation, the following specific cases are possible, called locks :

a) When determining the order difference, it may be necessary to shift the mantissa of one of the numbers by an amount greater than the number of digits in the discharge grid. In this case, naturally, such a number can be perceived as zero, and the further addition operation can be blocked, that is, not performed.

The maximum number is taken as a result.

Example :

  [m 

  ] 

  = 0.101 [M 

  ] 

  = 0.10111101
 [m 

  ] 

  = 1.001 [M 

  ] 

  = 0.10000001 

Order difference:

  00.101 = [m 

  ] 

  00.110 = [-m 

  ] 

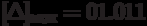- that is, this number is 11 ₁₀ , and in the discharge grid of the mantissa there are only 8 bits.

Therefore, the operation is blocked, and the result is a number:

  [m 

  ] = 0.101 [M 

  ] = 0.10111101 

A similar case may occur when the order difference is negative (negative overflow). In this case, the operation is also blocked, and the result will be a number with the maximum order.

Example :

  [m 

  ] 

  = 1.010 [M 

  ] 

  = 1.10101011
 [m 

  ] 

  = 0.110 [M 

  ] 

  = 1.11111111 

Order difference:

  11.010 = [m 

  ] 

  11.001 = [-m 

  ] 

  _______

  1 |  10.011
          one
    _______ 

10,100 =

That is, the difference in orders is less (-8).

The operation is blocked, and the result will be a number:

  [m 

  ] 

  = 0.110 [M 

  ] 

  = 1.11111111 

Decimal binary coded systems.

Sometimes computers use decimal number systems. It is beneficial to use them when the amount of input data for processing on a computer is large, the processing itself is carried out according to relatively simple programs. This results in a significant time saving, which follows from the fact that it is not necessary to do a transfer from decimal to binary and vice versa.

As a rule, the AU, which works with numbers in the decimal number system, is introduced into the equipment of such computers. Since a trigger cell with two stable states is used as the main storage element, each decimal digit is encoded by a set of binary symbols.

Conversion of numbers from the decimal system to the decimal binary-coded is performed extremely simply, bitwise and simultaneously across the entire grid:

  879.65_10 -> 1000 0111 1001, 0110 010110 ^ -2 

Similarly, a reverse translation is performed:

  0110 1001, 0101 0011 

  -> 69, 53 

There is a wide variety of decimal binary coded systems. This diversity results from the redundancy of the binary code, in which out of the 16 possible combinations in each digit, only 10 are used for the direct information purpose.

The most widely used are coding systems 8421 and 8421 ⁺³ (Stibitz code).

System 8421 is inconvenient because when performing the subtraction operation there is no direct transition from the digit of each digit to the additional code.

0000 - 0

0001 - 1

0010 - 2

0011 - 3

0100 - 4

0101 - 5

0110 - 6

0111 - 7

1000 - 8

1001 - 9

At the same time, this system has the additivity property, since the results of the addition operation over the numbers in the decimal system and over their image in the 8421 system coincide.

System 8421 ⁺³ - more interesting, because it has the property of self-completion. It is seen that the addition to 9 can be obtained by applying the bitwise inversion of the code.

0011 - 0

0100 - 1

0101-2

0110 - 3

0111 - 4

1000 - 5

1001 - 6

1010 - 7

1011 - 8

1100 - 9

In total there is A ₁₆ ¹⁰ = 2.9 • 10 ¹⁰ variants of the 10th binary-coded systems.