Lecture
Annotation: The lecture presents the minimization of incompletely defined functions, provides a synthesis of functions in Sheffer bar and Pierce arrow bases, gives approaches to the minimization of conjunctive forms.
Very often, if not in most cases, the operation of a particular device is described using an incompletely defined function, since some combinations of input signals are not given or are prohibited.
Definition An incompletely defined function is such a switching function, the values of which on some sets of arguments can be arbitrary (that is, equal to "0" or "1").
Definition Let the function f (x 1 , x 2 , ... x n ) not be defined on the "p" sets of arguments. Then a fully qualified function 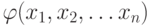 We will be considered equivalent to f (x 1 , x 2 , ... x n ), if its values on those sets on which f (x 1 , x 2 , ... x n ) is defined coincide.
We will be considered equivalent to f (x 1 , x 2 , ... x n ), if its values on those sets on which f (x 1 , x 2 , ... x n ) is defined coincide.
Obviously, there are 2 p different functions equivalent to f (x 1 , x 2 , ... x n ).
The minimization problem f (x 1 , x 2 , ... x n ) is to choose such an equivalent 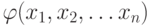 which has the simplest form.
which has the simplest form.
We introduce two auxiliary equivalent functions. 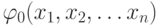 ,
, 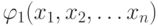 which take on forbidden argument sets the values 0 and 1, respectively.
which take on forbidden argument sets the values 0 and 1, respectively.
THEOREM . PDNF incompletely defined f (x 1 , x 2 , ... x n ) coincides with the disjunction of the shortest implicant 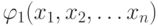 that co-cover all the constituents of the unit
that co-cover all the constituents of the unit 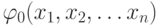 and none of which is superfluous.
and none of which is superfluous.
Example :
Let f (x 1 , x 2 , ... x n ) be given in the following table:
| f (x 1 , x 2 , ... x n ) | one | - | - | - | 0 | one | 0 | 0 | one | 0 | - | 0 | one | - | - | one |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Numeric equivalents of sets | 0 | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 | 13 | 14 | 15 |
Then
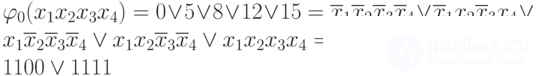 ,
,
but
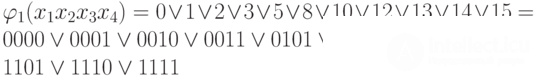
Find simple implicants 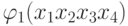
Constituent units  one one | Gluing marks | Implicants | Gluing marks | Implicants |
|---|---|---|---|---|
0000 | * | 000- 00-0 -000 | * | 00- - 00- - -0-0 |
0001 0010 1000 | * | * | ||
| * | * | |||
| * | 00-1 0-01 001- -010 1-00 | * | ||
0011 0101 1010 1100 | * | - | ||
| * | * | ten | ||
| * | * | |||
| * | * | |||
1101 1110 | * | -101 1-10 110- 11-0 | - | |
| * | ||||
* | - | eleven- - | ||
| - | ||||
1111 | * | 111- | * |
Simple implicants 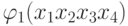
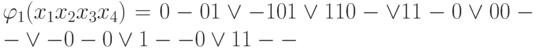
Construct an implicant matrix.
Constituent units 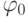 | 0000 | 0101 | 1000 | 1100 | 1111 |
|---|---|---|---|---|---|
Simple implicants 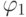 | |||||
| 0-01 | + | ||||
| -101 | + | ||||
| 110- | + | ||||
| 11-0 | + | ||||
| 00-- | + | ||||
| -0-0 | + | + | |||
| 1--0 | + | + | |||
| eleven-- | + | + |
Perform optimal coverage of the constituent unit 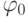 simple implicants
simple implicants 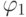 and we get the minimal form of the function f (x 1 x 2 x 3 x 4 )
and we get the minimal form of the function f (x 1 x 2 x 3 x 4 )
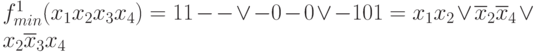
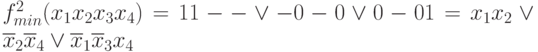
Minimization of incompletely defined functions with the help of Veitch diagrams in a visual and convenient form allows finding minimal forms.
Example :
Consider the function f (x 1 x 2 x 3 x 4 ) and find its minimal form. Fill in the Veitch diagram according to the following rules: put in the cells of the diagram units that correspond to the constituents of the unit, zeros for the absent constituents and the symbol of uncertainty - “*” (asterisk) - to the others.
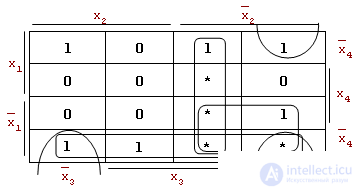
It can be seen that the cells for the constituents: x 1 x 2 x 3 x 4 , x 1 x 2 x 3 x 4 , x 1 x 2 x 3 x 4 it is advisable to “put” units instead of symbols of uncertainty, since in this case the correct rank 2 configuration, which is covered by the product x 2 x 3 .
Similarly, in the cell x 1 x 2 x 3 x 4 you need to "put" one.
So, 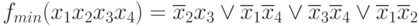 .
.
Remark Everything that has been said about minimizing the function represented in the PDNF or DNF is valid for the function specified in the CNF or CNF.
In this case, you need to find the correct configuration formed by zeros.
feight
(xone
, x2
)
| x 1 | 0 | 0 | one | one |
|---|---|---|---|---|
| x 2 | 0 | one | 0 | one |
| f 8 | one | 0 | 0 | 0 |
This function can be represented by writing down the "units":

or
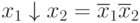
Based on the principle of superposition:
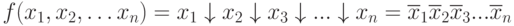
Applying the de Morgan rule:

or:
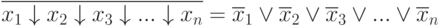
those.
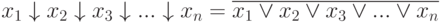
Consider some relationships for Pierce's operation:
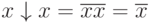

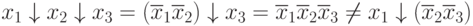 ,
,
those. Pierce operation does not have the property of associativity
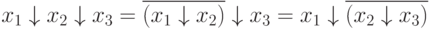
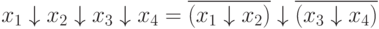
In this case, the order of operations in the formulas, where there is a Pierce operation is as follows:
Synthesis of logical functions in the Pierce basis is convenient to produce, having a function entry in the CNF.
Suppose that the FAL is given in conjunction form
f = Q 1 Q 2 Q 3 . . . Q n
Substitute the term Q i in the form:
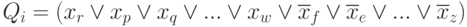
Take double negation from both sides of this equality, applying the de Morgan rule

Applying a ratio derived from the superposition principle:
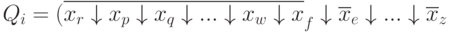
Or, applying this transformation to the original form, we get:
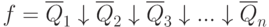
So: to move from the CNF to the Pierce basis and inversion, you need:
Example :

Remark Since in these works the number of letters does not increase, and if the initial form of the function was minimal, then the newly obtained will also be minimal (in fact, the situation is more complicated, since we are not considering a basis "  "and the other, that is"
"and the other, that is"  "and" - "- Pierce operation and inversion).
"and" - "- Pierce operation and inversion).
Fundamentally, you can get rid of the negatives by applying the ratio:  , but then it will not be possible to say that the form obtained will be minimal!
, but then it will not be possible to say that the form obtained will be minimal!
| x 1 | 0 | 0 | one | one |
|---|---|---|---|---|
| x 2 | 0 | one | 0 | one |
| f 14 | one | one | one | 0 |
Note that this function is dual with respect to f 8 , therefore all properties are essentially dual duality of the considered ones.
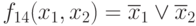 (write functions by zeros)
(write functions by zeros)
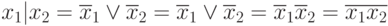
based on the principle of superposition:
x 1 | x 2 | . . . | x n = x 1 x 2 ... x n
Consider some equivalences:

x 1 | x 2 | x 3 = (x 1 x 2 ) | x 3 = x 1 | (x 2 x 3 )
x 1 | x 2 | x 3 | x 4 = (x 1 x 2 ) | (x 3 x 4 )
We formulate the rules for the transition from a DNF function to an expression using the operation "Sheffer Stroke".
Example :
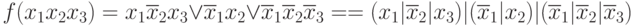
The same can be said about the minimal form.
In conclusion, it should be noted that at present the issues of the synthesis of functions in the singleton basis are of great importance, since the corresponding elements use the operation of Pierce and Schaeffer. However, the theoretical methods of synthesis are not fully developed in such detail as they were made in the basis of the “and”, “or”, or “inversion”.
As noted, in order to obtain the minimum form of the function, both MDNF and MISP should be constructed.
Consider the construction of the MCF.
Basically, the methods of obtaining MCPF are similar to the methods of obtaining MDNF and therefore we formulate only the rules for obtaining MCPF:
 ,
,
those. the function must be represented in the form of a conjunction of the missing number of disjunctive members with corresponding negatives.
deployment formulas:

. . . . . . . . . . . .
get SKNF.
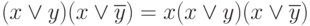
and absorption: 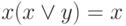 , get abbreviated CNF.
, get abbreviated CNF.
If possible, discard several members at once, act as if minimizing the function of the DNF.
Comments
To leave a comment
Digital devices. Microprocessors and microcontrollers. computer operating principles
Terms: Digital devices. Microprocessors and microcontrollers. computer operating principles