2.4 Minimizing Boolean Functions

The goal of minimization is to obtain a logical function equivalent to the given one, but containing the minimum number of corresponding logical variables. There are a lot of minimization methods, but we will consider only the most frequently used in practice.

Algebraic simplification is one of the ways to minimize logical functions, which uses theorems and the laws of Boolean algebra.

The minimization algorithm consists in finding and grouping a pair of “neighboring” sets of variables in order to reduce one variable according to the law of gluing. This process continues until not a single pair of adjacent sets remains. The final logical expression is simplified using gluing or absorption theorems.

However, algebraic simplification is usually used for simple certain functions. With a large number of variables and for incomplete functions, this method is practically unacceptable.

The Quine – McClasskey minimization is used with a large number of variables and a small number of fictitious states of Boolean functions. This is a tabular method based on sequential pasting of adjacent sets. The algorithm of this method is quite simple and therefore convenient for software implementation [10].

The minimization by the Carnot matrix method is used in cases where the original function contains no more than six to seven logical variables.

The possibilities of using Carnot matrices to minimize Boolean functions depend on the ability to select groups of cells of the matrix with the same states of functions, which are neighboring states of variables. Such groups of neighboring symmetric cells are called subcubes . Thus, a subcube is a set of matrix cells with the same function states, in which one or more variables have a constant value. The number of cells in a subcube must be equal to 2k, where k = 0, 1, 2, 3,. . . . Consequently, subcubes can be one-, two-, four-cellular, etc. When allocating a unicellular subcortical, no variable is excluded, since one cell of the matrix is ​​determined by one complete set; at allocation of two-cellular podkub one variable is excluded; with four cells, two variables are excluded, etc. Subcubes are symmetric solid or spaced rectangles. When allocating podkubov follow the following rules.

1. Matrix cells with the same function values ​​(only single or only zero) must be included in at least one subcube.

2. A subcube should unite as many cells of the matrix as possible (from a 2k series) with the same function value.

3. The dimensions of the subcube can be increased due to the inclusion of empty (fictitious) cells of the matrix.

4. The same cell of the matrix can be included in different subcubes, if it contributes to their expansion.

5. The number of podbubov should be minimal.

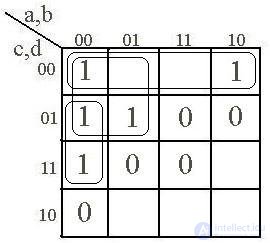
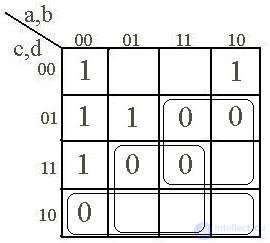
Fig. 2.2 Figure 2.3

The next step after minting podbubs is the minimization of logical formulas. Two options should be considered here:

a) the allocation of podkubov logical units;

b) the allocation of subcubes for logical zeros.

When allocating subcubes by units, the logical formula will be MDNF. The elementary minimum conjunction for each subcube is determined by variables that do not change their state in this subcube. The values ​​of the variables are recorded according to their state in the cells of the matrix. Conjunctions obtained for all subcubes disjoint, while receiving MDNF.

When allocating subcubes by zeros, the logical formula will be in the form of MCF. In this case, an elementary minimal disjunction is compiled for each subcube, and the values ​​of variables that have a constant state on this subcube are inverted. Further, elementary disjunctions are conjunctured to produce the MCF.

So, for the Boolean function known to us (Table 2.1), the Carnot matrix and the subcubes selected in them are shown in Fig. 2.2 and 2.3.

Singling out the subcubes in units, we get MDNF: Y = 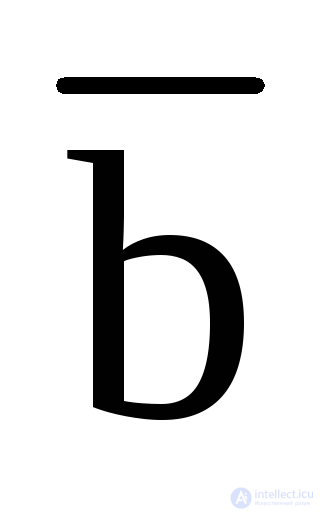d + + , the same - by zeros, we get the ICFM: Y = ( + d) ( + ) ( 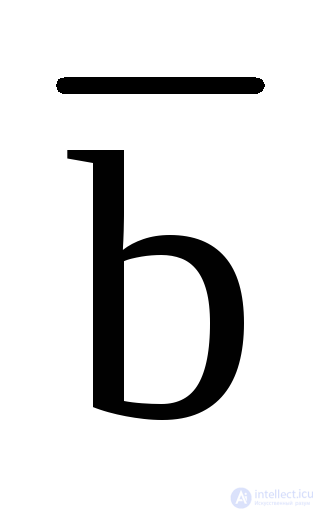+ ). Usually choose the option in which a smaller number of variables.

Control tasks

1. Convert an expression 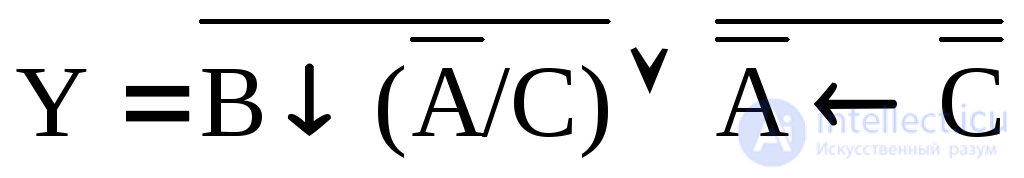in order to simplify.

2. Convert successively the left and right sides of the equation in order to prove the given identity:

.

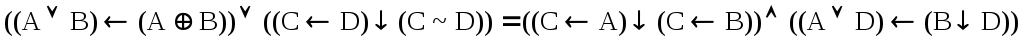3. Find the values ​​of each of the following Boolean functions for a = 1; b = 0; c = 0; d = 1: ; ; ; .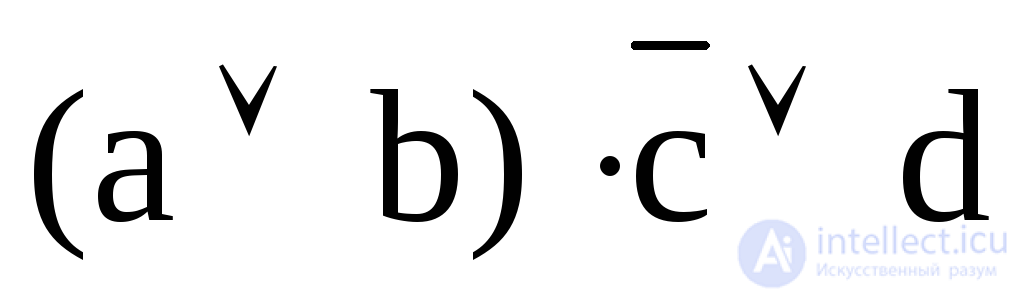

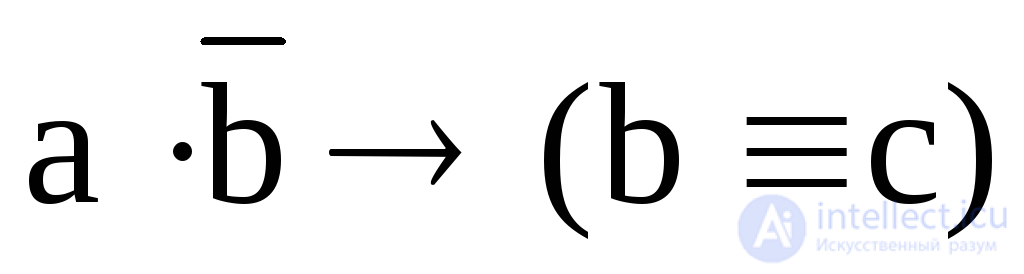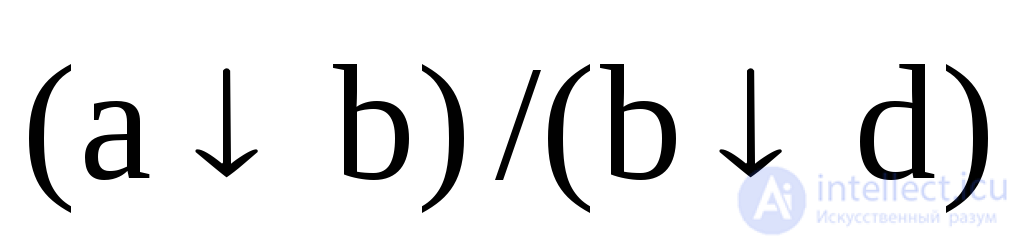4. Prove the validity of the identities:

; ; .

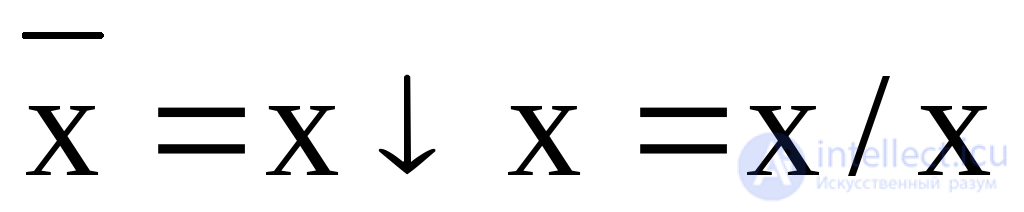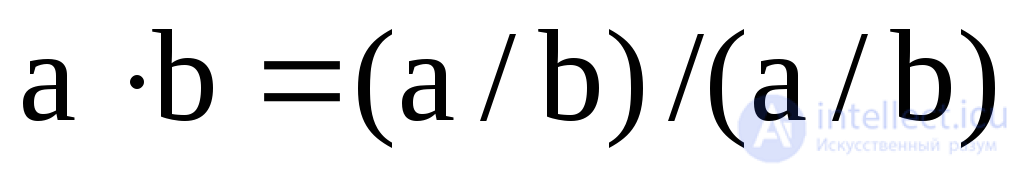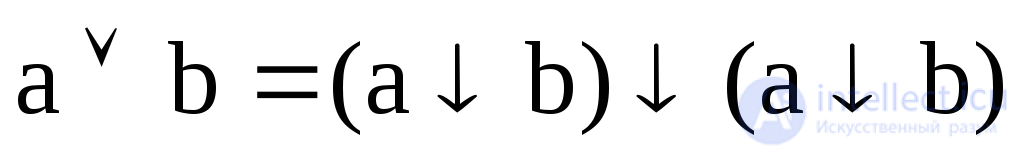5. Record all functions of two variables in perfect disjunctive and conjunctive normal forms.

6. Bring the given function to perfect disjunctive and conjunctive normal forms. .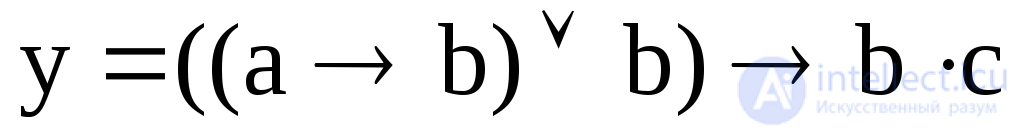

7. Convert an expression 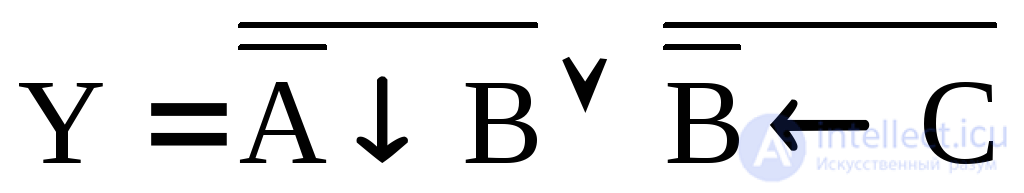, decompose the constituents of zero and one, present the state table and the Carnot matrix.

8. Logical function 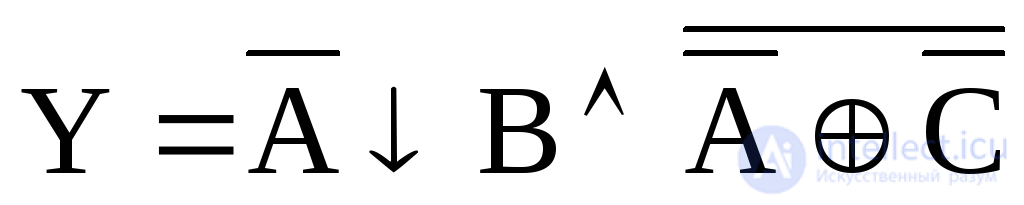transform and imagine using de Morgan's theorem using only the Webb function and only the Schaeffer prime.

9. Simplify the logical expression using the laws of Boole’s logic. Using truth tables, compare the simplified expression with the source: .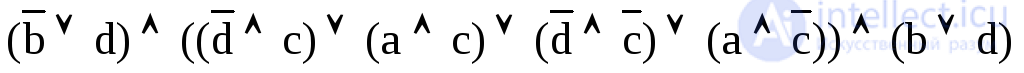

10 Analytically transform and simplify the left and right sides of the identity in order to prove it:

.

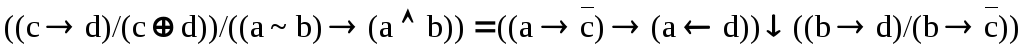11. Minimize the Boolean functions defined by decimal equivalents, using the Quine-McClassky, Gavrilov-Kopylenko methods and using Carnot matrices. Compare the results of minimization.

Y1 = {3,4,5,7,11,17,19,23,24,26,27}; YF = {1,2,6,8,10,12,13,16,21,22}.