5.6. Minimization of incomplete state machines

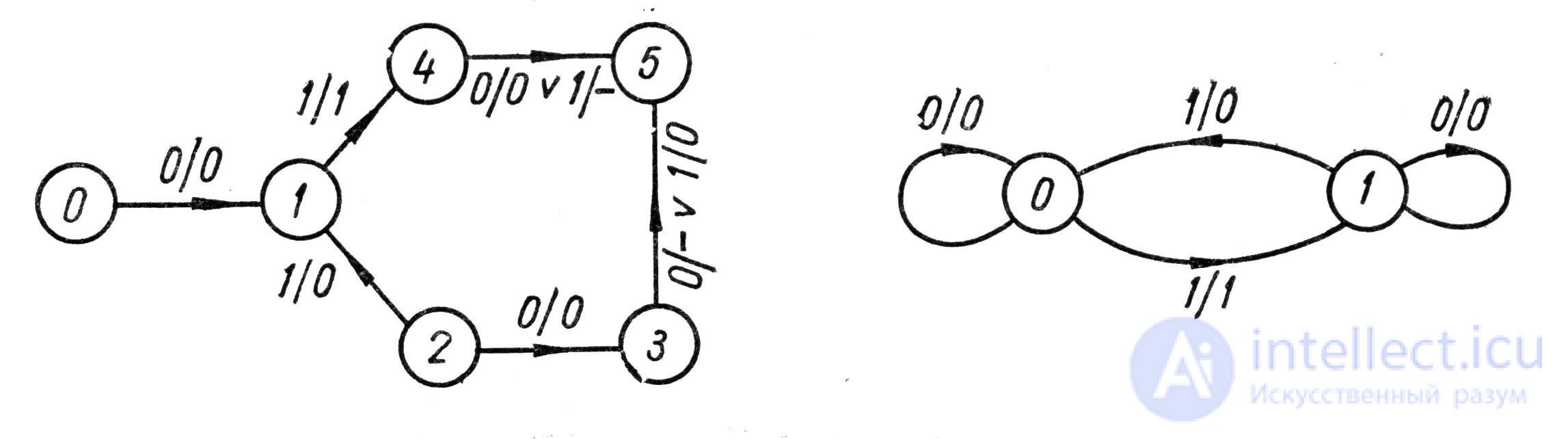
As mentioned in (5.4), the general transition table for incomplete automata contains dashes instead of states and exits for forbidden inputs, as well as instead of indeterminate exits. For example, for an incomplete automaton whose graph is shown in Fig. 5.11а, the general table of transitions - tab. 5.18.

Here, input 0 in states 1 and 5, as well as input 1 in states 0 and 5 are prohibited. In addition, in state 3 when exposed to 0 and in state 4 when exposed to 1, the outputs are not determined.

a) b)

Fig. 5.11

An input sequence is said to be valid for an automaton in the state q i , if it does not violate the restrictions on the input in any state of the automaton A and the output it generates is determined at the final cycle. On the other cycles of the input sequence, the outputs may not be defined, but the sequence of states must necessarily exist. For example, for the above automaton in state 0, the valid input sequence (0, 1, 0) generates the sequence of states {1, 4, 5} and the final output 0. At the same time, the sequence (0, 1, 1) is not valid, so as the final output is not defined.

The abbreviated form of the incomplete automaton A is such an automaton A ', which, in relation to the input sequences admissible for A, behaves at the outputs in the same way as the initial automaton A, but has a smaller number of states. An automaton A 'is said to be quasi-equivalent to an automaton A. The quasi-equivalence relation is reflexive and transitive, but not symmetric, i.e. has all the properties of the relationship of inclusion. Therefore, they also say that A ' includes A, and write A  A'. At the same time, A  A 'does not at all imply A'  A, which is sometimes expressed in words: A 'does the same and, maybe, more than A.

The problem of minimizing an incomplete automaton is reduced to finding a quasi-equivalent automaton that has the least number of states, and is solved as follows.

Table 5.19

First, on the set of states Q = { q 1 q 2 ... q r } of the original automaton determines the compatibility relation. States q i and q j is called with compatible if any input sequence admissible for these states does not generate different final outputs for initial states q i and q j , automaton. The compatibility relation is reflexive and symmetric, but not necessarily transitive. It follows that compatibility is a relation of tolerance. All states compatible with each other are combined into tolerance classes Q'0, Q'1, ..., Q'm, which form a covering of the set of states Q.

To determine compatible states, one can use a method similar to that described in (5.5). The source table contains pairs of states in which there are no different outputs for any valid input symbol. Cells corresponding to the forbidden inputs for this pair of states are filled with a dash and, with the exception of pairs, as described in (5.5), are not taken into account. So, for the automaton given by the transition table above, we have table 5.19.

The pair marked at the first step (0, 2} is the only incompatible pair in the table, as it is not contained in any other rows. Consequently, all unmarked pairs are incompatible. By constructing a tolerance matrix for compatible pairs and rearranging rows and columns in it, we have:

From here we select the tolerance classes Q'0 = {0, 1, 4, 5}, Q'1 = (0, 3, 4, 5}, Q'2 = (2, 3, 4, 5}, combining compatible with each other) states. Here, in particular, one can make sure that compatibility does not have a transitivity property, for example, pairs of states (0, 1} and {0, 3) are compatible, but states 1 and 3 do not belong to the same tolerance class and, therefore, they are incompatible.

It follows from the definition of compatibility and the method of obtaining tolerance classes that when exposed to any non-prohibited input symbol, the automaton from compatible states goes to the same or compatible states, and the outputs (if defined) will be the same. Thus, in our example, under the influence of 0, the classes Q'0 and Q'1 turn into {1.5], and Q'2 - into {3.5}; under the influence of 1, the class Q'0 turns into {4, 5}, Q'1 - into {5} and Q'2 - into {1,5}. Consequently, the initial automaton can be represented as a quasi-equivalent automaton in which the tolerance classes Q'0, Q'1, ..., Q'm correspond to the state q'0 q ' 1 ... q ' m. However, such an automaton will not always be minimal. To obtain the minimum form of the automaton, it is necessary to select the smallest number of such tolerance classes that form the coverage of the set of states Q and at the same time include the set of states following the states of each class for all non-prohibited influences. For the considered example, these requirements are satisfied by the classes Q'0, and Q'2, since Q'0 Q'2 = Q, and all sets of subsequent states {1,5}, {3,5}, {4,5} and {5} are subsets of Q'0 and Q'2. The corresponding minimum shape is shown in Fig. 5.11b, where the states 0 and 1 correspond to the classes Q'0 and Q'2.

Further simplifications relate not to the number of states, but to the structure of the sets that form the minimum coverage Q. If you can exclude some states from the selected tolerance classes so that the resulting subsets meet the above requirements, then these subsets also define another variant of the minimal form of the automaton. Thus, state 4 can be excluded from Q'0 or from Q'2, since it is included only in the set of subsequent states {4, 5}. Then we get two more variants of minimal coverages: {0, 1, 5}, {2, 3, 4, 5} and {0, 1, 4, 5}, {2, 3, 5}. But state 5 cannot be excluded from any class, although it is contained in each of them, since the sets of subsequent states {1, 5} and {3, 5} show that state 5 must be contained in both Q'0 and in Q'2.