5.5. Minimization of state machines

The transition from automaton A to equivalent is called an equivalent transformation of automaton A. Equivalent automata possess certain properties, even if they have a different number of states. In this case, an important task is the problem of minimizing the number of states of the automaton, or simply minimizing the automaton .

The minimization of the number of states of complete automata is related to the equivalence relation. Let automata A1 and A2, (these designations can refer to the same automaton) under the influence of any input sequence produce the same output sequence, that is, automata A1 and A2 in these states q i and q j indistinguishable by external exits. Such a relationship between the states of the same or two different automata has the properties of reflexivity, symmetry and transitivity, therefore, it is the equivalence relation of states. If the states are not equivalent, they are called distinguishable . Obvious justice of the following provisions:

1) q i states and q j the automaton is clearly distinguishable if the corresponding lines in the output table are distinguished;

2) q i states and q j the automaton is obviously equivalent if the corresponding lines in the transition table and in the output table are the same or become the same when replacing each number q i on q j (or vice versa).

The abstract minimization method for an automaton was proposed by Huffman. It is based on gluing equivalent states and consists in sequentially selecting the classes of equivalent states with the help of exit and transition tables. Consider the method of Hufman by example.

Let an automaton whose graph is shown in Fig. 5.10а, and the general table of transitions - tab. 5.12. It follows from this table that states from the set {0, 3, 4} are clearly distinguishable with any state from the set {1, 2, 5, 6}. Therefore, one should look for equivalent states only among the elements belonging to one of these sets. Since lines 0 and 4 are the same, and lines 1 and 5 become the same when replacing the numeral 1 by 5 (or 5 by 1) in the numerator, the pairs of states {0, 4} and {1, 5} are clearly equivalent.

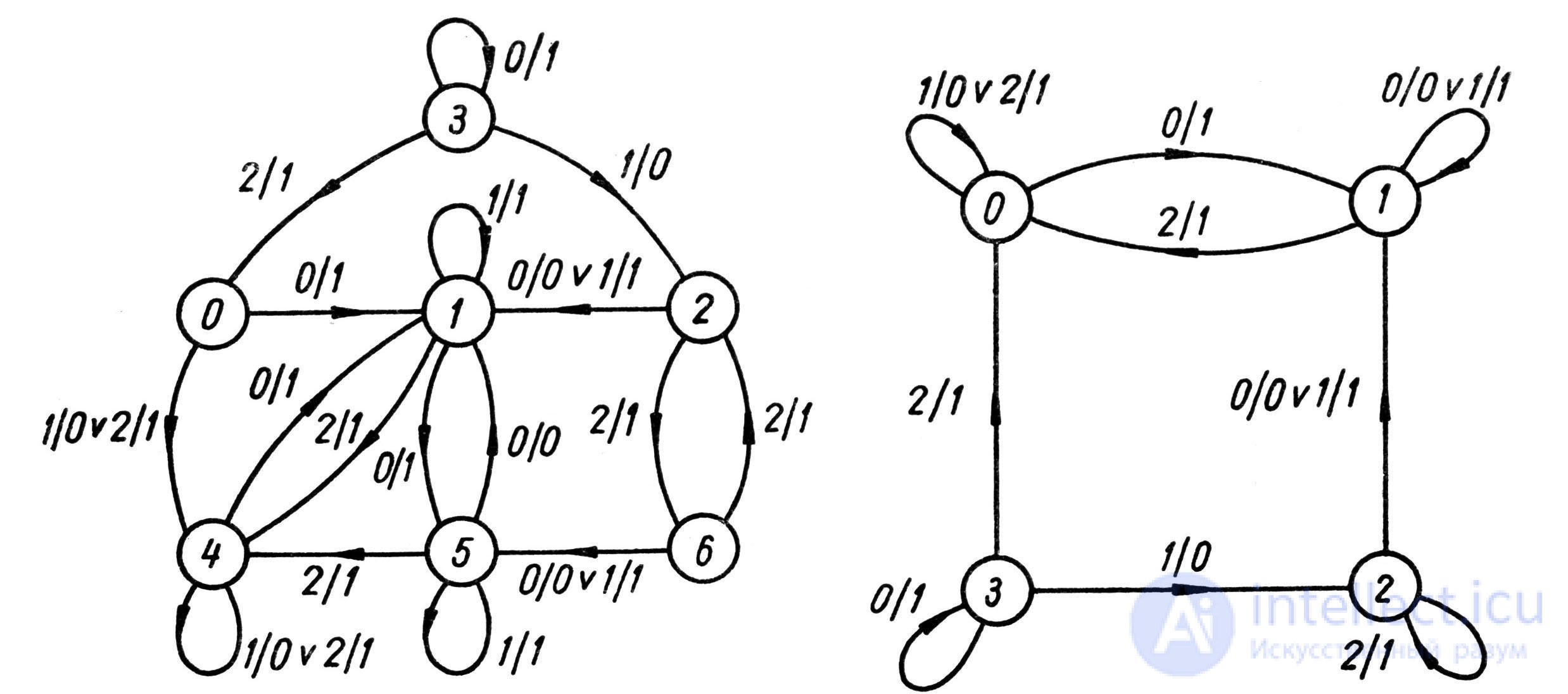
a) b)

Fig. 5.10

Table 5.12

Combining the equivalent states in the A1 automaton, we obtain an equivalent A2 automaton with a smaller number of states, which in any state cannot be distinguished from the original one by observing the signals at the outputs. Obviously, automata A1 and A2 are equivalent if each state q i automaton A1 corresponds to at least one equivalent state of the automaton A2 and if each state q j automaton A2 corresponds to at least one equivalent state of the automaton A1.

Table 5.13 Table 5.14

Equivalent states, for example, q i and q j , it is convenient to unite according to the general transition table, deleting the string q j and replacing everywhere in the numerator the numbers q j with q i . After combining pairs of obviously equivalent states, it may be possible to again detect such states, which are also combined using a similar procedure. As a result of sequential combining, we arrive at an abbreviated transition table, which corresponds to an abbreviated automaton equivalent to the initial one, but having a smaller number of states. So, for the example in question, we obtain the table. 5.13 and table. 5.14. Table 5.13 corresponds to the union of two pairs of equivalent states {0.4} and {1, 5}, and table. 5.14 - the union of one pair {2, 6}. The obtained minimum automaton contains only four states (Fig. 5.10b).

If all pairs of equivalent states of a finite automaton are known, then an equivalence relation is defined on the set Q of its states, which corresponds to a partition into equivalence classes. In this case, a state that does not have an equivalent state is an equivalence class, the only element of which is the state itself. Denote by q ' 0 q ' 1 ... q ' v are representatives of equivalence classes and, through A ', an automaton whose set of states is the family of representatives Q' = { q ' 0 q ' 1 ... q ' v }. It can be argued that automata A and A 'are equivalent (A ~ A'), and A 'has the minimum number of states, that is, it is the minimal form of the automaton.

The union of equivalent states into equivalence classes is quite simple. If q i ~ q j and q j ~ q k , then on the basis of the transitivity property it follows that q i ~ q k and, therefore, a pair { q i ~ q j } and { q j ~ q k } are included in their common equivalence class. But to identify all pairs of equivalent states, a more cumbersome procedure is required, since the set of such pairs is not exhausted by explicitly equivalent states and cannot always be fully discovered and combined in the manner outlined above.

For the equivalent partitioning of the set Q states of the automaton, a number of methods have been proposed. One of them is based on the sequential consideration of all possible pairs of states and the exclusion of those that are not equivalent. In this case, a pair of identical states { q i , q i }, which, due to the property of reflexivity, are obviously equivalent ( q i ~ q i ) are not considered. The procedure of equivalent splitting is carried out according to the table of pairs of states , which is obtained on the basis of the general automaton transition table. Since clearly distinguishable pairs of states (for such states, the rows in the output table are different) cannot be equivalent, they are not included in the pairs table. A line is assigned for each pair, a column for each input, and in the cells, based on the transition table, a pair of states is entered into which the automaton passes from this pair of states for a given input action (the order of recording the states in each pair is indifferent). Excluded pairs are marked in some way (typed in bold, underlined or labeled). The general table of transitions and the table of pairs of states of an automaton obtained from it are presented respectively as Table. 5.15 and table. 5.16.

Table 5.15 Table 5.16

Since the same rows of the output table correspond to the state sets {0, 2, 4, 6, 7} and {1, 3, 5, 8}, in the first column of the pair table only pairwise combinations of such states are included, which are one and the same the set, i.e. are not clearly distinguishable.

The elimination of pairs is based on the following position: if the state q i and q j are equivalent, then the states in which the automaton goes under any input action are equivalent. This means that in the first step, it is necessary to note those pairs that are transformed into pairs consisting of different states and not present in the first column of the table. Since the indicated pairs cannot be equivalent, the next step marks all those pairs that go into the pairs marked in the previous step, etc. The process ends when among the unmarked couples there are no such that can be noted in accordance with the stated rule. After that, the unmarked pairs are equivalent pairwise states.

In the example above, pairs (1, 8}, (3, 8} and {5, 8} are marked in the first step, {1.5} and {3, 5} in the second, {0, 4} in the third, {0, 6}, {2, 4), {2, 6}, {4,7} and {6, 7}. The unmarked pairs {0,2}, {0.7}, {1.3 are equivalent. }, {2,7} and (4,6), which form equivalence classes Q0 = (0, 2, 7}, Q1 = {1, 3} and Q2 = {4, 6). In addition, those not included in these the sets of states 5 and 8 form equivalence classes Q3 = {5} and Q4 = {8}. Denoting representatives of the resulting five classes, respectively, from 0 to 4, we obtain for the automaton under consideration a minimal form with five states and a general transition table (Table 5 .17).

Table 5.17 Table 5.18

It should be noted that an automaton whose all states are equivalent is reduced to an automaton with one state, that is, it is essentially a combinational circuit. An automaton, among which there are no equivalent states, is irreducible . If A 'is the minimal form of the automaton A, then it is unique and irreducible.