Lecture
Sets can be defined using operations on some other sets and subsets. Let given a certain set of objects, which can be described as a set
V = {a, b, c, d, e, f, g, h, i, j, k} .
Suppose that some of the objects, namely: a , b , d, and f are round, while some — b , c , d , h , and i — are painted white. In this case, it is said that the set V has two subsets A = { a , b , d , f } and B = { b , c , d , h , i } of round and white objects. One can say otherwise: the initial set is called fundamental or by the universe , and the subsets A and B are simply sets.
As a result, we get four classes of elements:
С 0 = { e , g , j , k } - elements that do not have any of the named properties,
С 1 = { a , f } - elements with only property A (round),
С 2 = { c , h , i } - elements possessing only property B (white),
С 3 = { b , d } are elements possessing simultaneously two properties.
It is convenient to depict operations on sets using a graphical Euler-Venn diagram (Fig. 1).
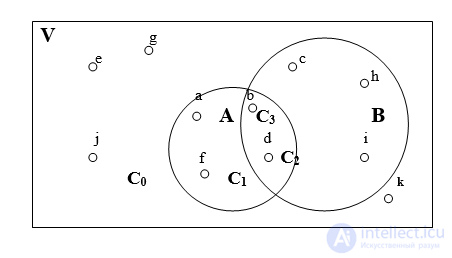
Fig. one . Euler-Venn diagram for two sets A and B
The union of the sets A = { a , b , d , f } and B = { b , c , d , h , i } let's call the set A  B = { a , b , c , d , f , h , i }. Thus, the union covers three classes of elements - C 1 , C 2 , C 3 , which are shaded in the diagram (Fig. 2). Moreover, both sets may not intersect; do not have common elements. The logical operation of combining two sets can be characterized in words: the element belongs to the set A or the set B. The fact that the element x belongs to A or B can be expressed by the formula
B = { a , b , c , d , f , h , i }. Thus, the union covers three classes of elements - C 1 , C 2 , C 3 , which are shaded in the diagram (Fig. 2). Moreover, both sets may not intersect; do not have common elements. The logical operation of combining two sets can be characterized in words: the element belongs to the set A or the set B. The fact that the element x belongs to A or B can be expressed by the formula
x A B = ( x A ) ( x B ),
Where  - a logical connection symbol or , which is called a disjunction .
- a logical connection symbol or , which is called a disjunction .
Intersection the sets A and B are called the set K = A B, containing those elements from A and B that are simultaneously included in both sets. For our example, we will have (Fig. 3):
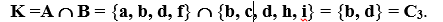
The fact that the element x simultaneously belongs to two sets A and B can be expressed by the formula
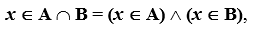
Where - the symbol of the logical connective and , which is called a conjunction.
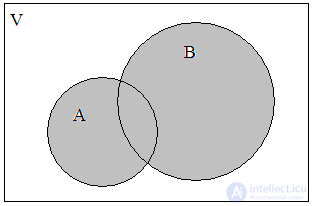
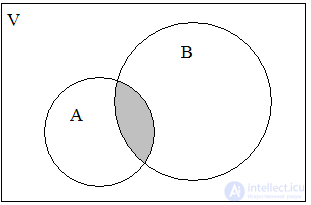
Fig. 2. A B Fig. 3. A B
Consider areas C 1 and C 3 , forming a set A (Fig. 4). Then the regions С 2 and С 0 form a set of elements that are not included in A (Fig. 5). This is referred to as  . The union or disjunction of sets A and
. The union or disjunction of sets A and  will give the whole universe V (A
will give the whole universe V (A  = V ) , and the intersection or conjunction will give us the zero set ; (
= V ) , and the intersection or conjunction will give us the zero set ; (  A = ) . So many
A = ) . So many  complements the set A to the universe V , hence the name - an additional set or addition as an operation. The operation of addition is also called inversion.
complements the set A to the universe V , hence the name - an additional set or addition as an operation. The operation of addition is also called inversion.
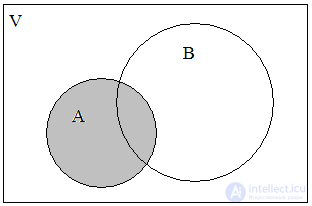
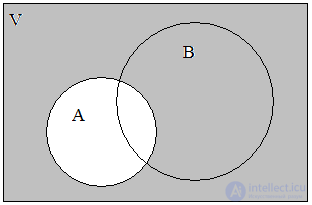
Fig. 4. A Figure five. 
After considering the inversion operation (addition), all four areas Сj on the diagram can be expressed as follows:
C 0 = 
 , C 1 = A
, C 1 = A  C 2 =
C 2 =  B , C 3 = A B.
B , C 3 = A B.
Using inversion, you can imagine any multiple operation, for example, a union:
A B = (A  ) (
) (  B) (A B) .
B) (A B) .
The operations of addition or inversion of the union and intersection of sets are called, respectively, the Pierce arrow ( D =  ) and the Schaeffer stroke ( K =
) and the Schaeffer stroke ( K = 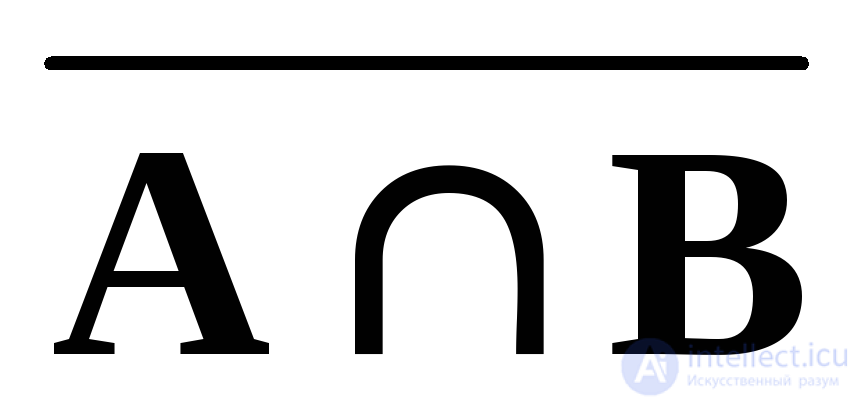 ) , which are denoted by A ↓ B and A / B respectively . The diagrams for these operations are shown in Fig. 6 and 7.
) , which are denoted by A ↓ B and A / B respectively . The diagrams for these operations are shown in Fig. 6 and 7.
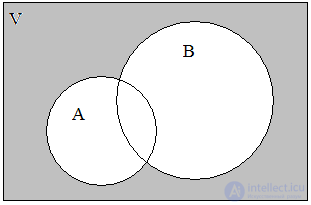
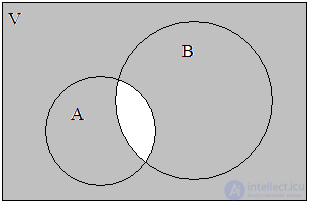
Fig. 6. A ↓ In Fig. 7. A / B
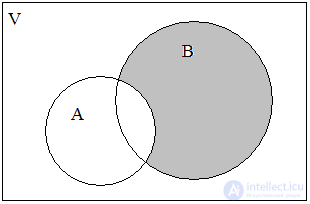
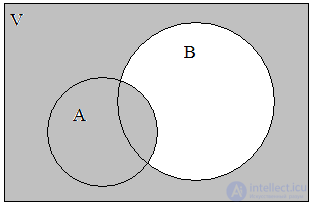
Fig. 8. ( In ← A ) Fig. 9. (B → A)
The difference between the sets B and A is the set of those elements of the set B that are not included in the set A (Fig. 8). Such an operation is also called prohibition A and is denoted ( B ← A ). For our case, this will be the C 2 region.
At the same time ( B ← A ) =  v .
v .
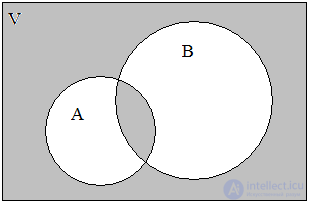
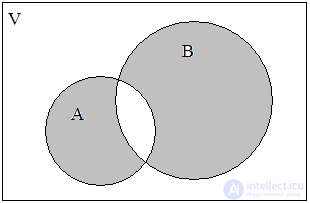
Fig. 10. ( A B) Fig. 11. ( A B)
An addition to the ban is the implication A. In the Euler-Venn diagram, this is a partial inclusion of the set B in the set A (Fig. 9). Denoted by such an operation (B → A) . At the same time (B → A) = A  .
.
bc
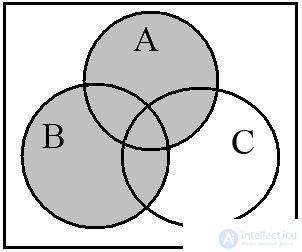
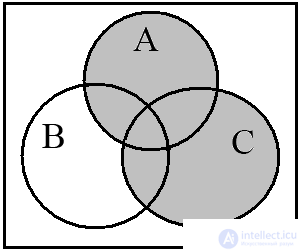
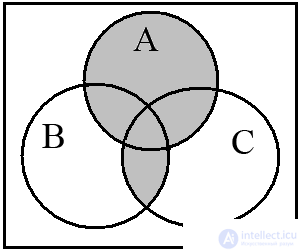
Fig. 12. (A B) (A C)
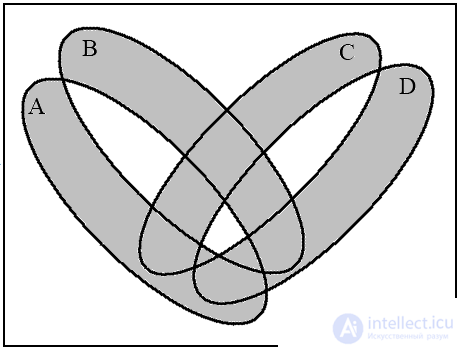
a ( A B ) b (( A B ) → ( C D ))
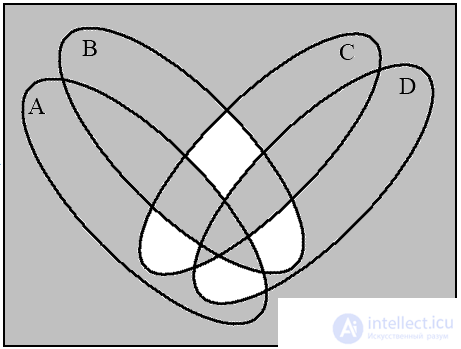
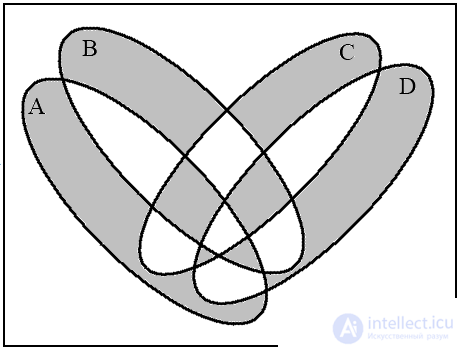
c (( A B ) / ( C D )) d (( A B ) → ( C D ))
(( A B ) / ( C D ))
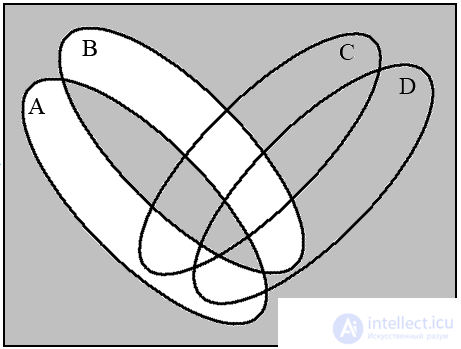
Fig.13. Venn diagrams for operations on four sets
The prohibition B (A ← B) = A is determined similarly.  and implication B (A → B) =
and implication B (A → B) =  v .
v .
It remains to cite two mutually complementary operations — a symmetric difference or an inequality and equivalence or equivalence.
Equivalence is determined by those elements of the sets A and B , which are common to them, as well as elements that are not included in either A or B. In our case, these will be the C 0 and C 3 regions (Fig. 10). Denotes the equivalence of A B or A ~ B.
A ~ B = ( 
 ) (A B) .
) (A B) .
Inequality is the union of two differences or two prohibitions. This operation is denoted ( A B) . In this way,
( A B) = (A ← B) ( B ← A ), or ( A B) = (  B) (A
B) (A  ) .
) .
In the Euler-Venn diagram, these are the C 1 and C 2 (Fig. 11). Inequality has the name strict disjunction . This operation can be expressed by the words: “either A or B ”.
Euler-Venn diagrams quite clearly illustrate operations on three and four sets. Consider the operation (A B) (A C) and construct the Euler-Venn diagrams for three sets. The diagram in fig. 12a depicts the operation (A B), and fig. 12b - (A C) . The conjunction of these relations is illustrated in the resulting diagram in Fig. 12c.
For four sets, four Euler circles do not give a complete Venn diagram, since their intersection gives only 14 regions, but 16 is necessary. Therefore, the circles must be deformed into ellipses. Let us show by example the construction of a diagram for the expression (( A B ) → ( C D )) (( A B ) / ( C D )) .
In fig. 13 depicts four diagrams corresponding to the indicated sequence of operations. The last diagram (Fig. 13d) is the resulting one.
Comments
To leave a comment
Finite state machine theory
Terms: Finite state machine theory