6.2. Basic requirements for algorithms

1 . The first thing to note in any algorithm is that it is applied to the source data and gives the results. In technical terms, this means that the algorithm has inputs and outputs. In addition, in the course of the algorithm, intermediate results appear that are used in the future. Thus, each algorithm deals with the data - input, intermediate and output. Therefore, together with the refinement of the concept of the algorithm, it is necessary to clarify the concept of data, that is, indicate what requirements the objects must meet in order for the algorithms to work with them.

It is clear that these objects should be clearly defined and distinguishable both from each other and from “non-objects”. In many cases, it is well understood what this means: such algorithmic objects include numbers, vectors, graph adjacency matrices, formulas. With objects such as a “good book” or “meaningful statement” that any person can easily manage (but each in their own way!), The algorithm will refuse to work until they are described as data using other, more suitable objects.

In the theory of algorithms, specific finite sets of source objects (called elementary) and a finite set of tools for constructing other objects from elementary are fixed. The set of elementary objects forms the final alphabet of the source symbols (numbers, letters, etc.) from which other objects are built. Words of finite length in finite alphabets (in particular, numbers) are the most common type of algorithmic data, and the number of characters in a word (word length) is a natural unit of measurement of the amount of information processed. A more complicated case of algorithmic objects is formulas. They are also defined inductively and are also words in the final alphabet, but not every word in this alphabet is a formula. In this case, usually the main algorithms are preceded by auxiliary, which check whether the source data meets the necessary requirements. Such a check is called parsing.

2 Memory is required for data placement. Memory is usually considered to be homogeneous and discrete, that is, it consists of identical cells, with each cell containing one character of the data alphabet. Thus, the units of measurement of the amount of data and memory are consistent. In this case, the memory can be infinite.

3 The algorithm consists of individual elementary steps, or actions, and many different steps from which the algorithm is composed, of course .

4 The sequence of steps of the algorithm is determined, that is, after each step, it is either indicated which step to take next, or a stop command is given, after which the operation of the algorithm is considered complete.

5 The algorithm must meet the performance requirement, i.e., stop after a finite number of steps, indicating what is considered to be the result. In particular, anyone who presents an algorithm for solving a certain problem, for example, calculating the function f ( x ), must show that the algorithm stops after a finite number of steps (as they say, converges) for any x from the task area f . However, it is much more difficult to verify the effectiveness (convergence) than the requirements set out in paragraphs. 1–4. In contrast, convergence is usually not possible to establish by simply viewing the description of the algorithm; there is no general method for checking convergence that is suitable for any algorithm A and any data x .

6 It is necessary to distinguish: a) the description of the algorithm (instruction or program); b) the mechanism for implementing the algorithm (for example, a computer), which includes means for starting, stopping, implementing elementary steps, outputting results and ensuring determinism, that is, controlling the course of the calculation; c) the process of implementing the algorithm, that is, the sequence of steps that will be generated when the algorithm is applied to specific data. We will assume that the description of the algorithm and the mechanism for its implementation are finite (memory, as already mentioned, may be infinite, but it is not included in the mechanism). The requirements for the finiteness of the implementation process coincide with the performance requirements (see clause 5).

Consider the following problem: given a sequence P of n positive numbers (n is a finite but arbitrary number); it is required to order them, that is, to construct a sequence R, in which these same numbers are arranged in ascending order. Almost immediately, the following simple way of solving it comes to mind: we scan P and find the smallest number in it; delete it from P and write it out as the first number of R; again we turn to P and find the smallest number in it; we assign it to the right to the obtained part of R, and so on, until all numbers are crossed out in P.

A natural question arises: what does “and so on” mean? For greater clarity, let us rewrite the description of the solution in a clearer form, breaking it up into steps and indicating transitions between steps.

Step 1 . We are looking for the smallest number in P.

Step 2 . We find the found number on the right of R (at the initial moment R is empty) and delete it from R.

Step 3 . If there are no numbers in P, then go to step 4. Otherwise, go to step 1.

Step 4 . The end. The result is to consider the sequence R constructed to this moment.

Many will find such a description sufficiently clear (and even too formal) to use it clearly to get the desired result. However, this impression of clarity rests on some implicit assumptions, to which we are accustomed to correctness, but which are not difficult to break. For example, what does “sequence of numbers” mean? Is such a sequence ; ; 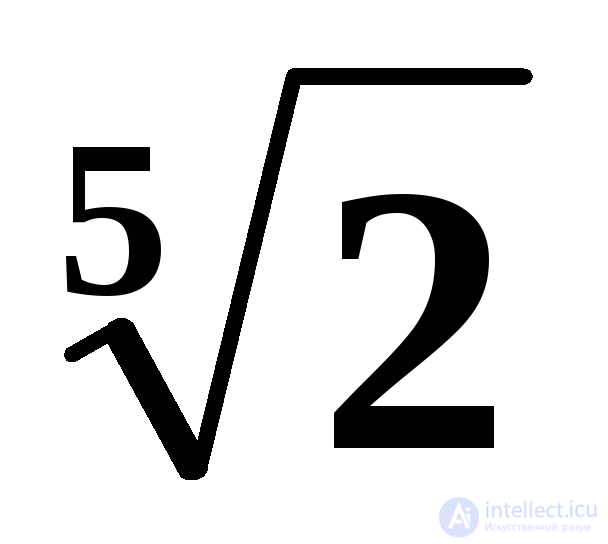(1,2) π? Obviously, yes, but in our description nothing is said of how to find the smallest number among such numbers. It does not tell at all about how to look for the smallest numbers; it seems that it is assumed that we are talking about numbers represented as decimal fractions and what is known how to compare them.

Therefore, it is necessary to clarify the data presentation forms. After all, for each representation there is its own alphabet (which, in addition to numbers, may include commas, brackets, operation and function signs, etc.) and its own way of comparing numbers (for example, the method of decimal conversion), while the finiteness of the alphabet requires fixing it is predetermined, and the finiteness of the algorithm description allows to include in it only a predetermined fixed number of comparison methods. Fixing the representation of numbers as decimal fractions also does not solve all problems. Comparison of 10 - 20-bit numbers can no longer be considered an elementary action: one cannot immediately say which number is greater: 908115577001.15 or 32899901467.0048. In machine algorithms, the representation of a number still requires further clarification: it is necessary, first, to limit the number of digits (digits) in a number, since it depends on how many memory cells the number will occupy, and second, agree on how to place the decimal point in a number, i.e., choose a representation in the form of a number with a fixed or floating point, since the methods of processing these two representations are different. Finally, anyone who has dealt with programming will note that in step 1, two things are required: the smallest number itself (to write it in R) and its place in P, i.e. its address in the part of the memory where P (to cross it out of P), and therefore you need to have the means to indicate this address.

Thus, even in this simple example, a simple analysis shows that the description, which looks quite clear, is still far from the algorithm. We are faced with the need to clarify almost all the basic characteristics of the algorithm, which were noted earlier: the alphabet of the data and the form of their representation, the memory and the placement of the elements P and R in it, the elementary steps (since step 1 is clearly not elementary). In addition, it becomes clear that the choice of the mechanism of implementation (say, a person or a computer) will also affect the very nature of the specification: a person has memory requirements, data presentation and elementary steps much weaker and “enlarged”, some minor details clarify yourself.

Perhaps, only two requirements to the algorithms in the above description are met sufficiently (they create the impression of clarity). The convergence of the algorithm is fairly obvious: after performing steps 1 and 2, either the work ends, or one number is deleted from P; therefore, exactly after n executing steps 1 and 2, all numbers will be deleted from P and the algorithm will stop, and R will be the result. In addition, determinism is not in doubt: after each step it is clear what to do next, if we take into account that here and in the future the generally accepted agreement is used - if the step does not contain instructions for further transition, then we perform the step following it in the description.