6.5. Turing Machine

In essence, the algorithm is a mechanical process of information processing. When executing an algorithm in an intuitive sense, we can use potentially unlimited memory, remembering the necessary information in the process of executing the algorithm as necessary, for example, making notes on a piece of paper. At the same time, the main limitation of a finite automaton is the finiteness of the number of its states, and therefore its memory. It can be assumed that this is why the finite state machine cannot be used as a model of a device that executes arbitrary algorithms.

If we add to the KA model the ability to memorize arbitrarily large amounts of information, then its capabilities for executing algorithms will expand and we will get an automaton with more extensive capabilities for information transformation. Alan Turing in 1936 defined the concept of an algorithm, based on the concept of an automatically operating machine, and proposed a formal model of a calculator, which is the result of simply adding potentially infinite memory to a finite state machine. He proposed a formal model of such a device that simulates the actions of a person solving a problem, guided by some algorithm. This device was called the Turing machine.

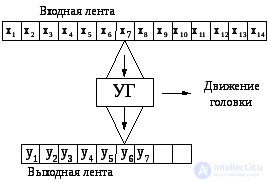
Fig.6.3

Consider the difference between a Turing machine and a simple model of a finite state machine. A finite state machine can be thought of as a device with a finite number of internal states Q = { q 1 , q 2 , ..., q k}, operating with two tapes: an input with a finite alphabet X = { x 1 , x 2 , ... , x n} and output with the final alphabet Y = { y 1 , y 2 , ..., y m } (fig. 6.3). The state machine works in cycles. On each clock cycle, it reads a symbol from the input tape cell being viewed with a certain input head, changes its state and prints some character of the output alphabet into the output tape monitored cell, after which its two read and write heads are moved one position to the right. The description of the functioning of a finite automaton can be considered as its program, which is actually an enumeration of the arguments and the corresponding values ​​of the partially defined transition function and outputs of the automaton δ: Q × X → Q '× Y.

Man has a finite memory, and in this sense it can be represented by a system with a finite number of states. The initial information to the algorithm is usually represented in the form of a finite sequence of characters (in the form of a word in the final dictionary). When executing the algorithm, the human calculator uses additional memory (which can be potentially infinite, such as sheets of paper) to record information, and this record is produced by it sequentially, character by character. In calculations, a person can return to the previously recorded information, erase some information, etc. Thus, the elementary operations during the execution of the algorithm can be considered recording and erasing a symbol, as well as shifting attention from one section of the recording to another.

The formal model proposed by Turing consists of: 1) a control device that can be in one of the states that form a finite set Q = { q 1 , q 2 , ..., q k}; 2) tapes divided into cells, in each of which finite alphabet characters X = { x 1 , x 2 , ... , x n} can be written; 3) devices for accessing the tape, i.e. the reading and writing head, which is shifted by a cell to the left or to the right or remains in place. The formal model proposed by Turing differs from the finite state machine in two aspects: it has one infinite work tape with which it reads and where it writes symbols, and a read / write head that can move along the work tape in any direction (see Fig. 6.4).

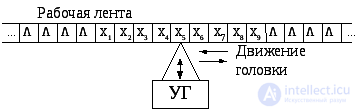
Fig.6.4

Each cell of an unrestricted tape can store only one character of the alphabet X, called the external alphabet of the machine. The work of the machine takes place in cycles. At each cycle, a single cell is viewed and the readable symbol x i is replaced by another x j , which is determined by the state of the machine q v at a given clock point from the set of its possible states Q ( i = j means that the symbol does not change; we will erase the character as empty symbol Λ). In addition, the subsequent state of the machine is generated q v +1 and a tape control command that prepares the next cell for viewing at the next cycle. There are only three such commands in the Turing machine: R - look at the cell next to the right, L - look at the cell next to the left, and E - continue to look at the old cell. The set of symbols Q = { q 1 , q 2 , ..., q k} and D = {R, L, E} forms the inner alphabet of the machine. Among the states of the control device MT, the initial state q 1 and the final stop state , which will be denoted by the symbol "!" In the initial state of the machine is before work; hitting the final state, the car stops.

The description of the functioning of the MT can be considered its program, which is represented by a finite set of arguments and the corresponding values ​​of the partially defined transition function and outputs δ: Q × X → Q '× X' × D.

The Turing machine has one final working alphabet X, in which the input and output characters do not differ, since the output character printed on the tape can be read by the machine in subsequent cycles. For convenience, it is usually assumed that the alphabet X also contains an empty symbol Λ, which fills all the cells of the working tape to the left and right of the final string of “significant” characters at the beginning of work.

The complete state of the Turing machine, by which it is unambiguously possible to determine its further behavior, is determined by its internal state, the state of the tape (that is, the word written on the tape) and the position of the head on the tape. The complete state will be called a configuration , or a machine word, and denoted by a triple α1 q v α2, where q v is the current internal state, α1 is the word to the left of the head, and α2 is the word formed by the symbol read by the head, and characters to the right of it, moreover, to the left of α1 and to the right of α2 all the cells of the tape are filled with empty symbols Λ.