4.2. Basic definitions of graph theory

The concept of a graph is used for the mathematical description of such situations when there are two sets, say V and X, and the elements of the set X play the role of bundles connecting pairs of elements of the set V.

For the precise definition of a graph, let us recall the concept of a predicate. Let P (x, y, z) be a triple predicate, so-called. “Ordered triple” of elements that are in some respects R. Then the exact definition of the graph is that it is a collection of two sets and a predicate indicating which pair of elements of the first set is connected by one or another element of the second set. It is considered that a graph G (X; V; P) is given if the set V ≠  and the set X are given, moreover (V  X ≠ ), and the three-place predicate P defined on all such ordered triples of elements v i , v j and x , for which v i  V, v j  V and x  X. Moreover, the elements of the set V are called vertices of the graph, and the elements of the set X are edges. The statement P ( v i ; x ; v j ) reads like this: an edge x connects a vertex v i with a vertex v j , or connects an ordered pair v j v j vertices.

Predicate P is called a graph incidentor . Otherwise, we can say that a graph is a collection of two sets V and X, between the elements of which the incidence relation is defined , each element x  X is incident to exactly two elements v i  V and v j  V.

Graph image: Graphs, as already noted in the examples, there is a way to "visualize" the connections between certain objects, which are represented as graph vertices. The vertices of the graph are depicted in the form of circles (sometimes in the form of points), and the edges of the graph (connection) - in the form of lines connecting the vertices.

x x 1 x 2

v i v j v i v j

but. b.

Fig. 4.2

It is said that the edge x connecting the vertices v i and v j is incident to these vertices, and the vertices themselves are incident. If the order of the vertices is not significant, i.e. If the graph's incidentor can be written as P ( v i ; x ; v j ) and P ( v j ; x ; v i ), then x is considered an undirected edge, and the graph is called a undirected graph, or neo-graph . In this case, the vertices incident to the edge are equal (Fig. 4.2a).

Often the connections between objects are characterized by a well-defined orientation. For example, on some streets only one-way car traffic is allowed, the positive directions of currents are set in the connecting wires of an electric circuit, relations between people can be determined by subordination or seniority. Oriented links characterize the transition of a system from one state to another, different relations between elements, for example, numbers (inequality, divisibility).

If such a ratio is determined by a graph, then the order of the vertices in such a graph is significant. In this case, the vertices incident to each edge are unequal and the incidentor must be written uniquely [P ( v i ; x ; v j )]. The edge x is called an oriented edge or an arc of a graph, coming from the vertex v i and entering the vertex v j , and the graph is called oriented or digraph. In this case, v i is called the initial vertex (beginning), and v j - the final vertex (end) of the arc x . The direction of the arc is indicated by an arrow. If the initial vertex masters the final vertex, i.e. edge or arc of a graph is incident to the same vertex, then such an arc is called a loop (Fig. 4.2b ) . In this case, the graph is called a loop graph, or pseudograph.

The lines representing edges or arcs of the graph may intersect, but the intersection points are not vertices. Graphs can be infinite, but we will consider finite graphs, i.e. with a finite set of their elements. Each edge of the graph is incident to exactly two vertices. A graph is called simple if each pair of vertices is connected by only one edge (Fig. 4.3a). If in a graph at least one pair of vertices connects several edges, then such a graph is called a multigraph (Fig. 4.3b).

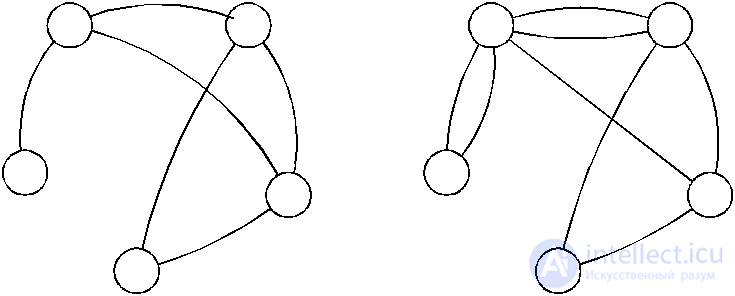
a) b)

Fig. 4.3

In a multigraph, different edges can be incident to the same pair of vertices, in this case they are called multiple (Fig. 4.4a). An orgraph may also have multiple edges (Fig. 4.4b), as well as edges that are incident to the same vertices, but running in different directions (Fig. 4c).

a B C)

Fig. 4.4

If a pair of vertices is connected by two or more arcs, then such arcs are called parallel. In this case, two arcs, equally directed with respect to a given vertex, are called strictly parallel, and differently directed - non-strictly parallel. It is clear that non-strictly parallel arcs that reflect the orientation of the connection in both directions are essentially equivalent to an unoriented connection and can be replaced by an undirected edge. Thus, each undirected graph can be associated with a digraph with the same set of vertices, in which each edge is replaced by two arcs having opposite directions. This correspondence is called canonical. An example of canonical correspondence is shown in Fig. 4.5.

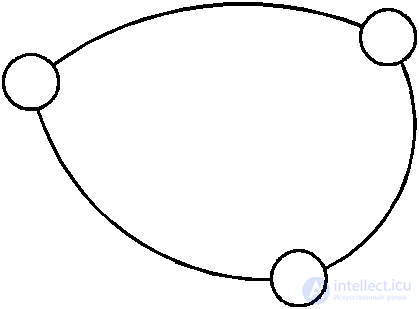
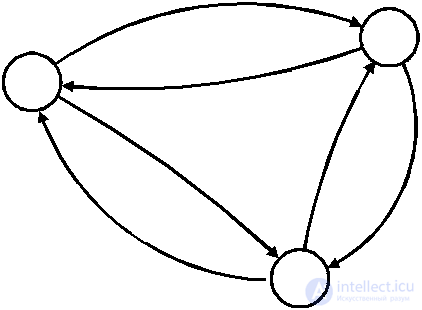
Fig. 4.5

A graph that contains both edges and arcs is called mixed . Any undirected or mixed graph can be transformed into an oriented replacement of each edge by a pair of weakly parallel arcs. If we change the directions of all arcs of the digraph to the opposite, then we obtain the digraph inverse to the original one.

If a vertex is not incident to any edge, then it is called isolated. A graph in which all vertices are isolated is called empty, or a null graph (Fig. 4.6).

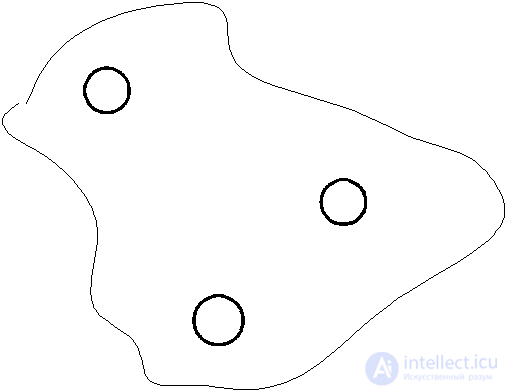
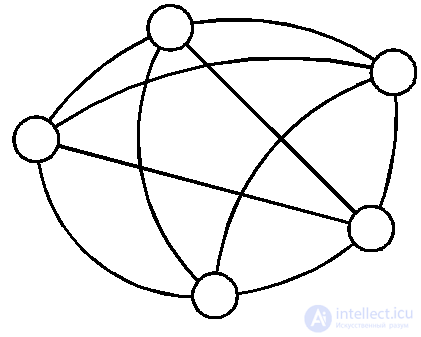
Fig. 4.6 Figure 4.7

For a simple graph, there is another extreme case where all possible connections connecting all vertices are edges. Such a graph is called complete (Fig. 4.7).

A graph is called flat (planar) if it can be laid in a plane so that its edges do not intersect anywhere.

The local degree of a directed graph G at a given vertex v i is the value of ρ ( v i ), equal to the total number of edges and arcs entering and exiting from this vertex. For a digraph, the local degree is determined by the formula

ρ ( v i ) = ρ + ( v i ) + ρ– ( v i ),

where ρ + ( v i ) is a positive half-degree (the sum of outgoing arcs),

ρ– ( v i ) - negative half-degree (sum of incoming arcs).

If in the graph the local powers of each vertex are equal to the same number - m , then such a graph is called a homogeneous graph of degree m . This graph is also called regular . A complete graph with n vertices is always homogeneous of degree n - 1, and an empty graph is homogeneous of degree 0. Any complete graph can be homogeneous.