2. Boole Logic 2.1. Boolean functions

The apparatus of Boolean logic, or else the algebra of logic , operates with logical variables that can take only two values: 0 and 1. Logical variables define a certain logical relationship, which is commonly called a Boolean function . The set of all Boolean functions and operations on them forms a Boolean algebra or algebra of logic. Boolean functions, or otherwise functions of the algebra of logic (FAL), can also take only two mutually exclusive values ​​0 and 1. When formally considering the laws of Boolean algebra, logical variables are usually denoted by lowercase Latin letters or assigned to them by identifiers.

Logical values ​​0 and 1 cannot be interpreted as numbers, arithmetic operations cannot be performed on them, since the algebra of logic is not an algebra of numbers, but an algebra of states. Nevertheless, in Boolean algebra, logical actions are performed on variables, which determine the nature of logical functions. The basic logical actions correspond to the simplest operations on sets: inversion , or negation, disjunction , or logical addition, and conjunction , or logical multiplication. Based on these three logical actions, all arbitrarily complex logical functions are constructed. In this case, the functions of one and two variables that play a very important role in Boolean algebra should be emphasized. With the help of these functions, using the principle of superposition, any logical function of any complexity of any number of variables can be described.

The principle of superposition is that each argument of a logical function can be a function of other logical variables, namely: if there is a function f { x 1; x 2; x 3}, then it is possible that x 1 = ( x 4, x 5).

Boolean functions of one variable are only four.

1. Zero ( const ”0”) F = X  = 0 - the value of the function is zero, whatever the value of the input variable.

2. Inversion (not) F = - the value of the function is the inverse of the value of the input variable.

3. Repetition (yes) F = X - the function value repeats the value of the input variable.

4. Unit ( const "1") F = X  = 1 - the value of the function is equal to one for any value of the input variable.

Of all the functions of two variables, ten are independent and depend both on variable a and on variable b. Moreover, the functions Y5, Y6 differ from the corresponding Y7, Y8 only by the order of the arguments. Thus, only eight of the 16 boolean functions of the two variables are original.

1. Y1 = a  b 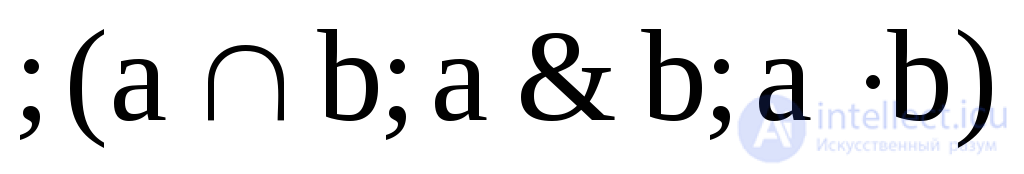- conjunction , logical "and";

2. Y2 = a  b 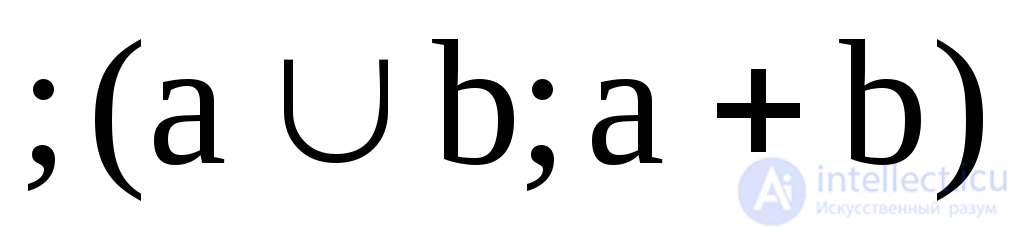- disjunction , logical "or";

3. Y3 = a / b 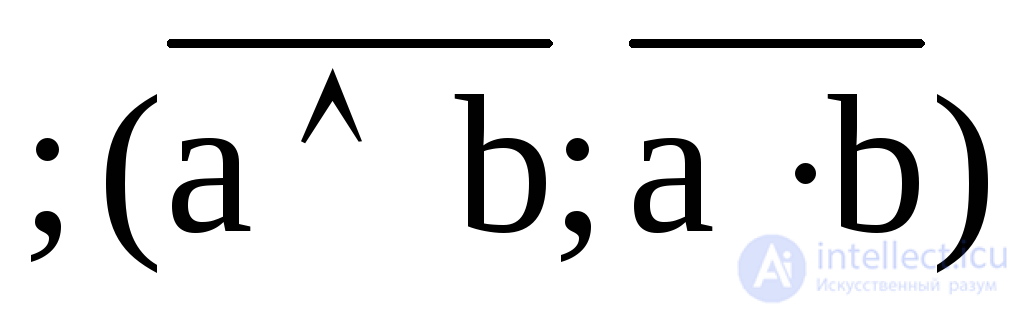- Sheffer's stroke , logical "and-not";

4. Y4 = a  b 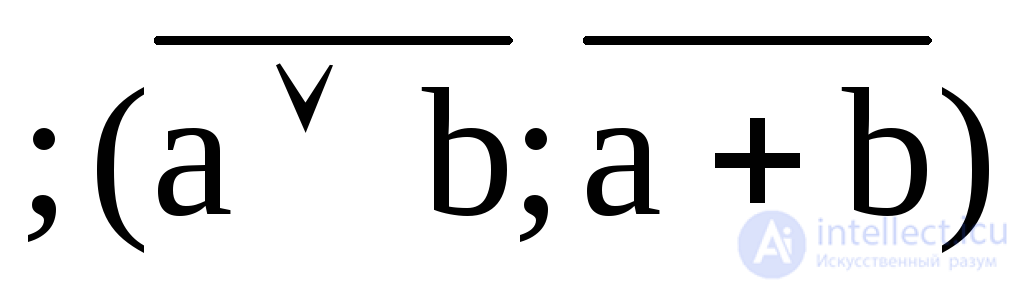- Pierce's arrow (Webb function), “or - not”;

5. Y5 = a b 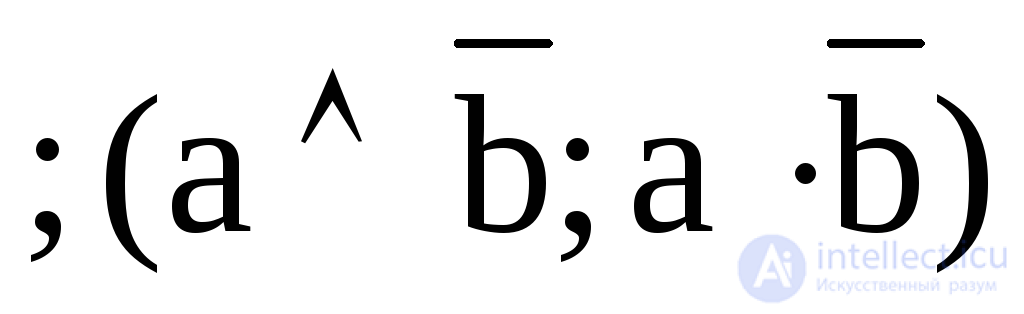- ban b, “a, but not b”;

6. Y6 = a b 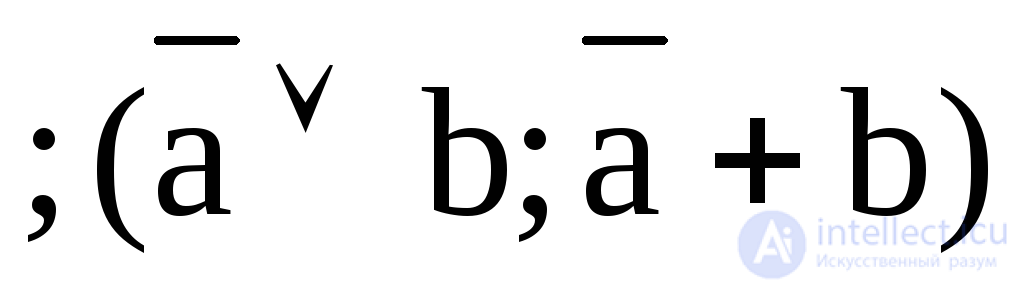- implication b, “if a, then b”;

7. Y7 = ba 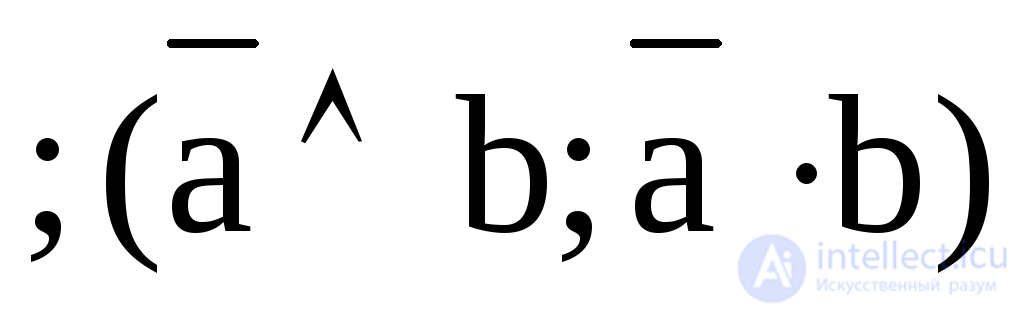- prohibition a, “b, but not a”;

8. Y8 = ba 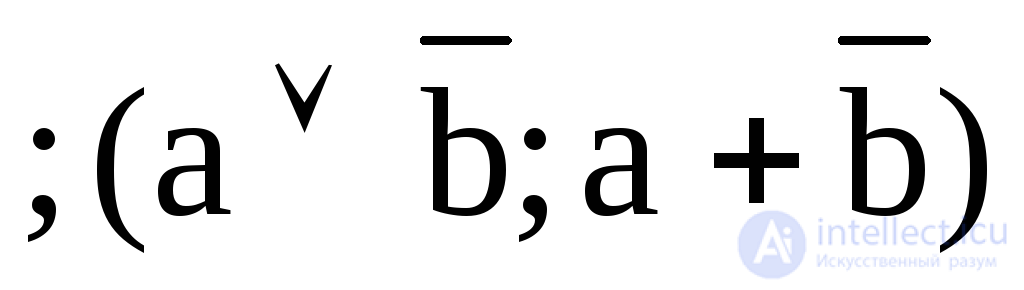- implication a, “if b, then a”;

9. Y9 = a  b 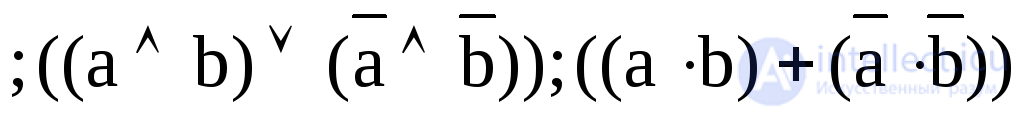- equivalence

equivalence;

10. Y10 = a  b 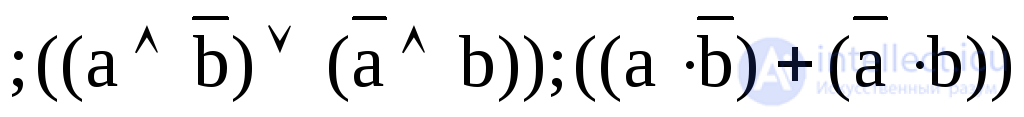- inequality ,

"Modulo 2".

2.2. The postulates and basic laws of Boolean algebra

Boolean algebra, like any mathematical science, is based on several axioms, or postulates. 

1. If x ≠ 1, then 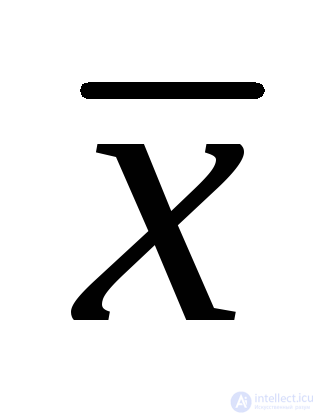= 0; if x ≠ 0, then 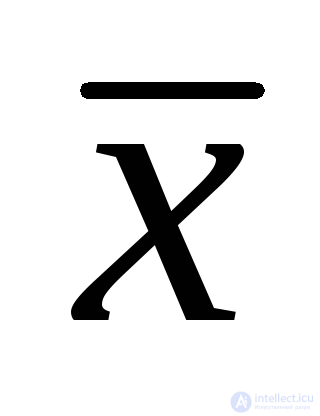= 1 (mutual exclusion axiom).

2. 0  0 = 0; 0  0 = 0.

3. 0  1 = 0; 0  1 = 1; (1 0 = 0; 1  0 = 1).

4. 1  1 = 1; 1  1 = 1.

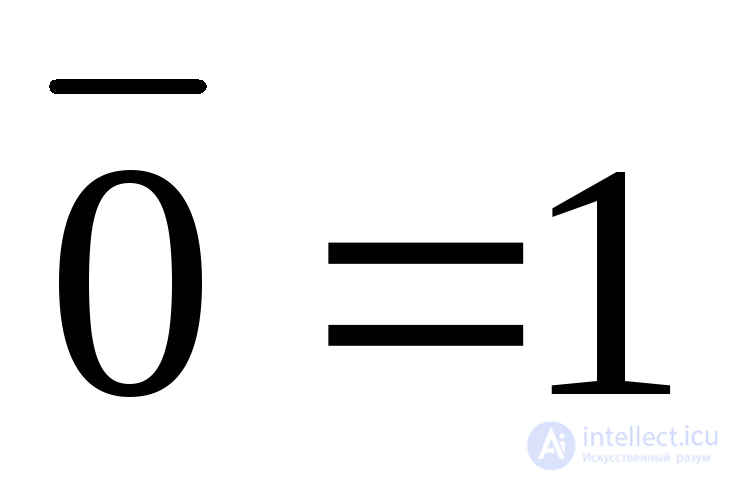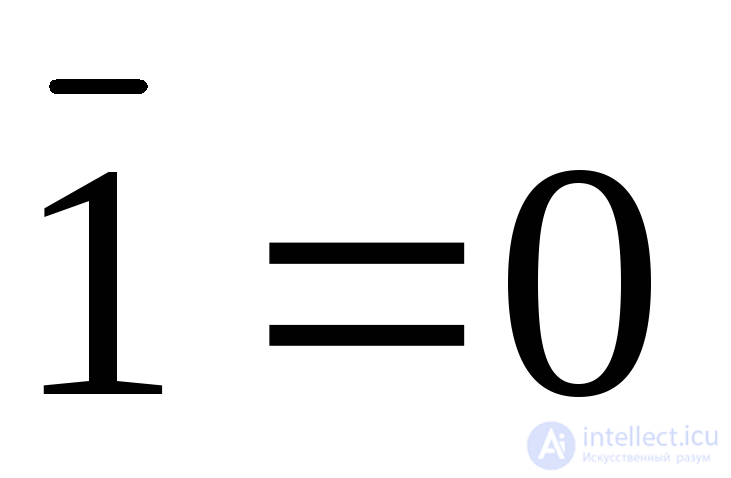5. ; (inversion).

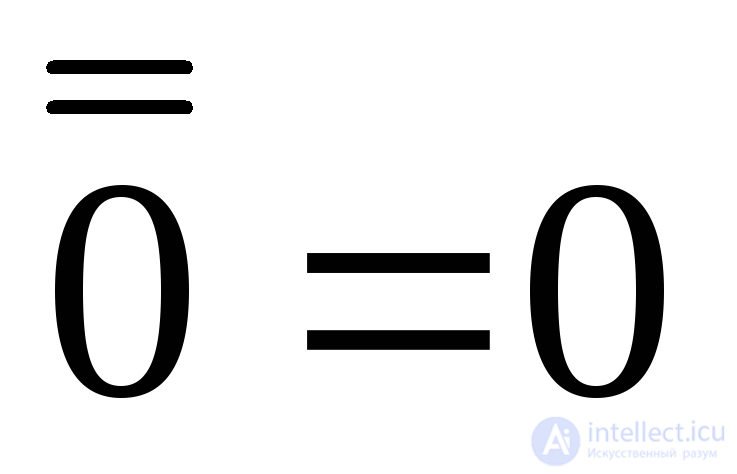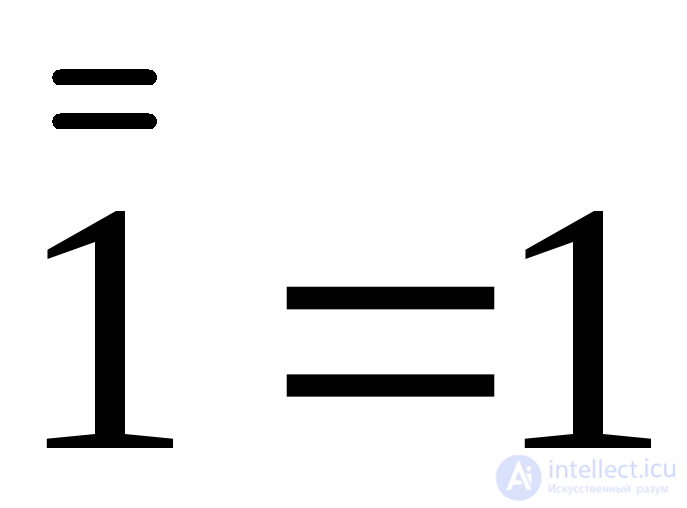6. ; (double inversion).

As the basic laws of Boolean algebra most often use the following (laws and theorems are given without proof).

1. A zero set: 0  a = 0; 0  a  b …  x = 0;

0  a = a

2. The universal set : 1  a = a;

1  a = 1; 1  a  b  c …  x = 1;

3. Idempotency (repetition): a  a  a …  a = a;

a  a  a  ...  a = a;

4. Additionality (contradictions): a  = 0; a  = 1;

5. Double inversion : = a;

6. Commutativity ( commutative ): a  b = b  a;

a  b = b  a;

7. Associativity (combinational): a  (b  c) = (a  b) c;

a  (b c) = (a  b)  c;

8. D istributivity (distributive): a  (b  c) = (a  b) (a  c);

a  (b c) = (a  b) (a  c);

9. Absorption : a  (a b) = a;

a  (a b) = a;

10. Bonding : (a  b)  (a 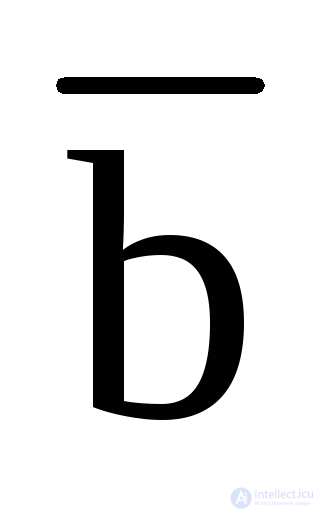 ) = a;

(a  b)  (a 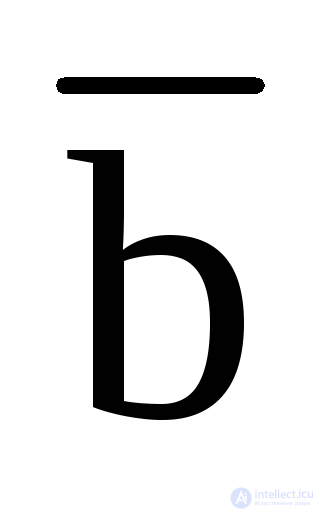 ) = a;

a  (  b) = a  b;

a  (  b) = a  b;

11. Inversions (theorem de Morgán): ;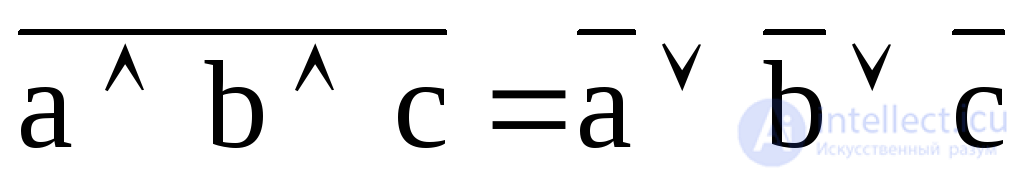

;

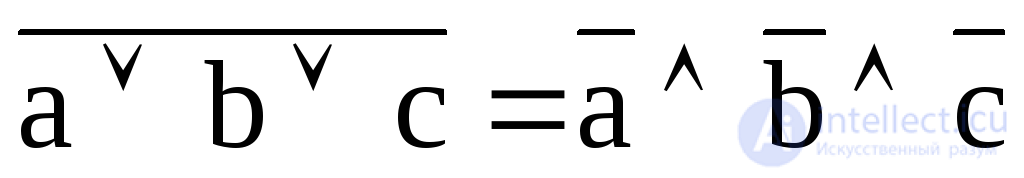12. Shannon's theorem : in order to obtain the inversion of some PLL, it is necessary to take the inversions of the variables and replace the disjunction operations with conjunctions and vice versa:

if there is Y = f (a, b, c, ..., x, , ), then = f ( , , ..., ,,  ) ..

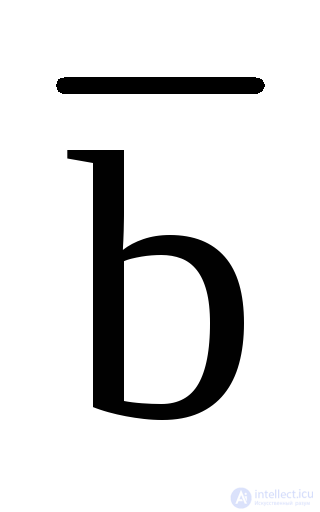
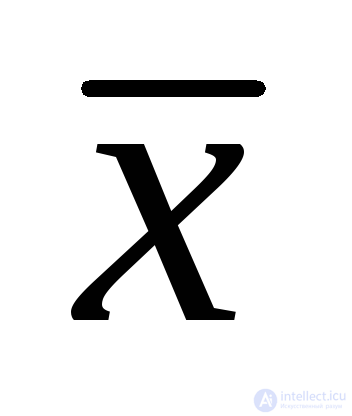13. Decompositions : f (a, b, c, ..., x) = [a  f (1, b, c, ..., x)]  [  f (0, b, c, ..., x)];

f (a, b, c, ..., x) = [a  f (0, b, c, ..., x)]  [  f (1, b, c, ..., x)].

The laws and theorems of Boolean algebra are necessary to transform and simplify logical functions, to prove the identity and equivalence of functions, as well as to represent Boolean functions in various forms.