3.2. Predicates and Quantifiers

From a logical point of view, binary objects that we considered in the algebra of logic (Boolean) are statements that can be true or false. Formulas are compound statements, the truth of which is determined by the truth of their elementary statements (A, B or C) and logical operations on these elementary statements (inversion, conjunction, disjunction, implication, etc.).

Predicate - this is a functional statement. Predicate logic is an extension of propositional logic by using predicates as logical functions. These functions are somewhat different from boolean functions. The Boolean function is homogeneous , i.e. for it, the range of values ​​of the function and the range of changing the arguments by type are the same — logical (either true or false ). For predicates, the range of the function is logical, and the range of changing the arguments is objective, hence the conclusion that this function is non-uniform.

Thus, the function P that takes one of the values ​​(0 or 1) and whose arguments can take any number of values ​​from an arbitrary set M will be called the predicate P in the subject domain M. The number of arguments of the predicate P ( x 1 , x 2 , ..., x n ) is called its order.

We give examples of predicate functions. Suppose there are a number of simple statements:

P1 = x 1 > A, P2 = x 2 > A, ..., Pn = x n > A.

Instead of the statements P1, P2, ..., Pn, you can enter a single predicate P ( x ) for which the variable x would take values ​​from the domain - x = { x 1 , x 2 , ..., x n }, and the predicate function itself would be written :

P ( x ) = " x > A".

Now we will change the original series of statements to another:

P1 = x 1 > y 1 , P2 = x 2 > y 2 , ..., Pn = x n > y n .

Here you can enter the double predicate P ( x, y ) = "x> y" with the additional subject area y = { y 1 ,, y 2 , ..., y n }.

We introduce the triple predicate P (x, y, z), which, say, means that “x is the sum of y and z ". If any variable is given a specific value, say x = 5, then the triple predicate will turn into a double P (5 , y , z) = P ¢ (y , z) = "5 is the sum of y and z.

For x = 5 and y = 3 we get a single predicate:

Р (5 , 3 , z) = Р¢ (3 , z) = Р Р (z) = "5 is the sum of 3 and z.

Finally, if we add the condition z = 2, then the original predicate becomes a zero-place predicate (constant or expression), which in this case takes the true value:

Р1 = Р (5,3,2) = "5 is the sum of 3 and 2" = 1.

But it could happen that z = 1, then there would be a false statement: Р0 = Р (5,3,1) = "5 is the sum of 3 and 1" = 0.

Thus, when the variable xi is replaced by the subject constant ai, the n-local predicate P ( x 1 , ..., x i , ..., x n ) is transformed into ( n - 1) -done predicate P ( x 1 , ..., a i , ..., x n ). By assigning specific values ​​to all the arguments of the predicate function, we thereby obtain the predicate constant.

The functional nature of the predicate entails the introduction of another concept - the quantifier . Let P ( x ) be a predicate defined on some set “M”. The statement: “for all x  M the value of P ( x ) is true” is denoted by the symbol  x and is called the quantifier of generality (“ All ” ). Another saying: “there is at least one meaning x  M, for which P ( x ) is true ”is called the quantifier of existence and is denoted by the symbol  x ( “ Exist ” ). By exposing quantifiers to predicates, we kind of strengthen or weaken their action.

On the other hand, the expression  x P ( x ) = 1 means that the conjunction of all values ​​of the predicate function is 1:

 x P ( x ) = P ( x 1 )  P ( x 2 )  P ( x 3 )  ··· = 1.

Similarly, the existence quantifier before the predicate  x P ( x ) = 1 means that the disjunction of all values ​​of the predicate function is 1:

 x P ( x ) = P ( x 1 )  P ( x 2 )  P ( x 3 )  ··· = 1.

Both quantifiers can be expressed one through the other on the basis of the law of De Morgan:

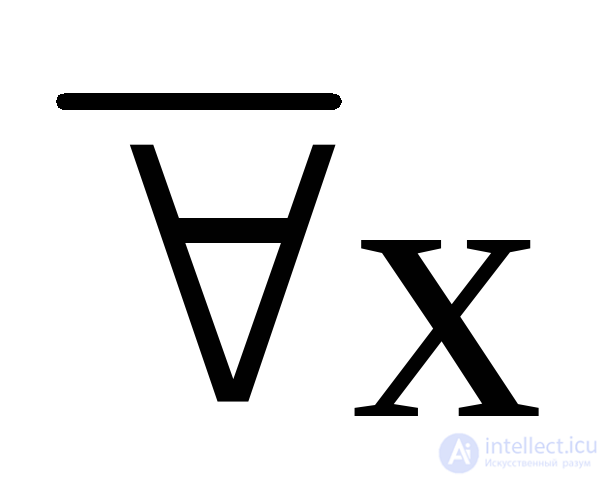P ( x ) = 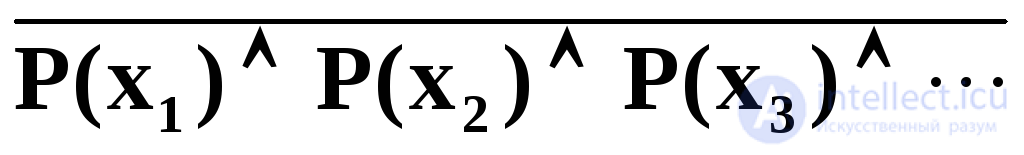= ( x 1 )  ( x 2 )  ( x 3 )  = x ( x )

 x P ( x ) = 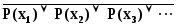= ( x 1 )  ( x 2 )  ( x 3 )  · = x ( x ).

From here

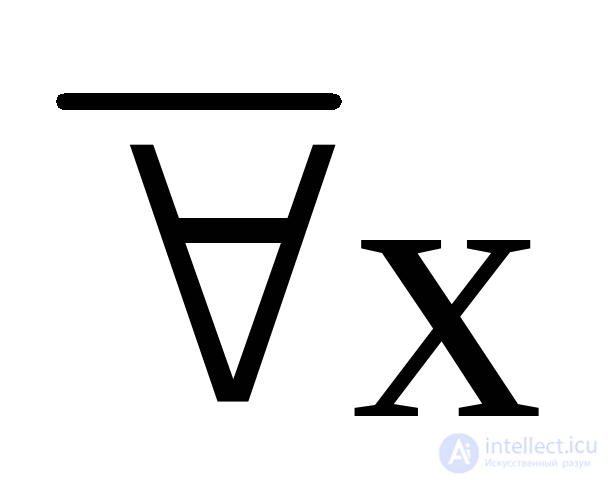
( x ) =  x P ( x ) and ( x ) =  x P ( x ).

The transition from P ( x ) to  x P ( x ) or to  x P ( x ) is called the binding of the variable x , as well as hanging the quantifier on the variable x . The variable on which the quantifier is hung is called a bound variable; unbound variable is called free. A free variable is an ordinary variable that can take any value from the set M.

If the expression P ( x ) is a variable statement depending on the value of x , then the expressions  x P ( x ) or  x P ( x ) do not depend on the variable x and, for fixed values ​​of P and M, they turn the single predicate into a statement.

You can hang quantifiers on multiple predicates, and in general on any logical expressions. The expression on which the quantifier is hung is called the quantifier scope . Hanging a quantifier on an n-place predicate reduces the number of free variables in it, turning it into an (n - 1) -space predicate. If we hang k quantifiers on an n-seater predicate, then it turns into a (n - k) -space predicate.

For example, let P ( x ) = " x be an even number." Then the statement  x P ( x ) is true on any set M of even numbers and is false if M contains at least one odd number. The statement  x P ( x ) is true on any set containing at least one even number, and false on any set of odd numbers.

Consider the double predicate P ( x , y ) = " x ≥ y " on the sets M. Hanging the quantifier  x ( x ≥ y ), we obtain a single predicate from y - "For all x from the set M, the statement" x ≥ y "is true . If M is a set of positive numbers, then this predicate is true at a single point with y = 0. If we hang a predicate on the second variable  x  y ( x ≥ y ), then we get the truth only on a set consisting of one element.

The main task of predicate logic is to establish the truth of predicate identities and logical consequences. Let us prove, for example, the distributivity of a quantifier  x with respect to a conjunction and a quantifier  x with respect to disjunction, i.e.

 x (P1 ( x ) P2 ( x )) =  x P1 ( x )   x P2 ( x ).

Let the left part of the expression be true for some P1 and P2, then for any a  M true P1 ( a )  P2 ( a ), therefore P1 ( a ) and P2 ( a ) are simultaneously true for any a. Therefore, the right side of the expression is also true.

If the left side is false, then for some a  M either P1 ( a ) or P2 ( a ) is false, and therefore either  x P1 ( x )  or  x P2 ( x ) is false, that is, the right part is false.

The identity is proved similarly.

 x (P1 ( x ) P2 ( x )) =  x P1 ( x )   x P2 ( x ).

However, if a community quantifier is used in conjunction with a disjunction, and the existence quantifier is used with a conjunction, then there will be a logical consequence

 x (P1 ( x ) P2 ( x ))  x P1 ( x )  x P2 ( x ).

And similarly

 x (P1 ( x ) P2 ( x ))  x P1 ( x )  x P2 ( x ).

Control tasks

1. There is a geometry theorem about three perpendiculars: "The straight line drawn on the plane perpendicular to the projection of the oblique, perpendicular to the most oblique." Whether this theorem is equivalent to the following assertions (У1): "A straight line drawn on a plane is not perpendicular to an inclined one, not perpendicular to its projection" and (U2): " A straight line drawn on a plane is perpendicular to an inclined, perpendicular to its projection" .

Note: Select in each statement simpler statements, namely: let statement (A) be: "The straight line on the plane is perpendicular to the inclined one" , saying (B) will be: "The straight line is perpendicular to the projection of the oblique one . " Then the structure of complex statements - theorems and statements В1 and У2, - can be represented by logical formulas: АВ,  and VA. To solve the problem, it is now sufficient to verify the equivalence of the corresponding formulas.

2. Suppose that the following theorem is true: “ The Petri net is consistent and invariant only if it is alive and limited ”. How to prove this theorem? Determine which of the following statements are consequences of this theorem:

a) Petri net is limited only if it is invariant ;

b) the inconsistency of the Petri net is a sufficient condition for its lack of vitality and limitations;

c) if the Petri net is not coordinated, then it cannot be non-living, but at the same time limited.

3. (The case of recidivists). Three recidivists, A, B and C, are suspected of a crime. The following facts are irrefutably established:

a) if A is guilty and B is innocent, then C participated in the case ;

b) C never acts alone ;

c) And never goes to work with C ;

d) no one except A, B and C is involved in the crime, but at least one of these three is guilty .

Is it possible on the basis of these facts to charge the B? Against B or C? Against A?

4. Write in the form of a predicate statement:

a) “ If two objects from M possess the property P, then they are the same” ;

b) “ At least one student solved all the problems ”;

c) “ Every task was solved by at least one student.”

5. Using the predicates, express the following statements and their negations: a) “ One and only one object has the property P ”;

b) “ At least two objects possess property P” .

6. Express with the help of predicates the following statements:

1. All elements of the array b [ j : k ] are zero.

2. Not a single element of the array b [ j : k ] is non-zero.

3. some elements of the array b [ j : k ] are null .

4. all zero elements of array b [0: n - 1] are in b [ j : k ] .

5. array b values [0: n - 1] are arranged in ascending order.

7. Predicates are defined on the set of natural numbers: P (x) = "the number x is divisible by 8" and Q (x) = "x is an even number". Read the following statements and find out their truth:

a)  xP (x); e) ;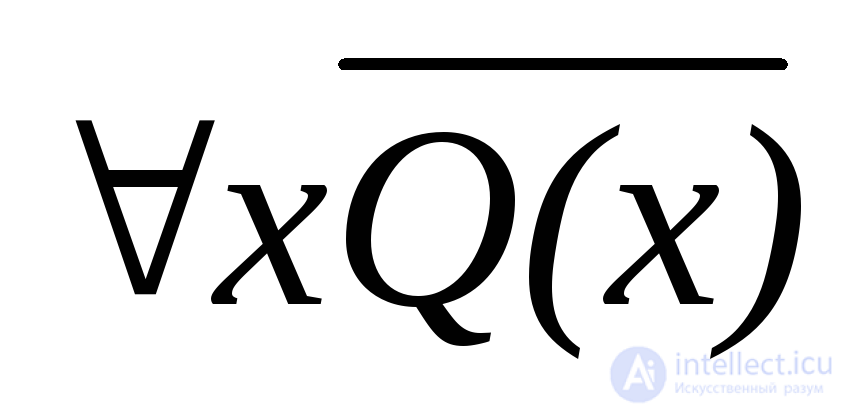

b)  xP (x); e)  x (P (x) Q ( x ));

c)  x Q ( x ); g)  x ( Q ( x )  P (x));

d) 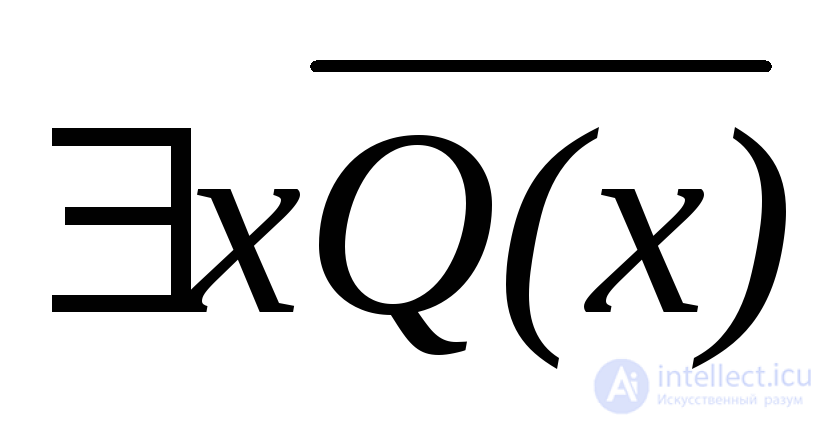; h)  x ( Q ( x )  P (x)).