Lecture
Lecture questions:
1. Comprehensive quality indicator
2. Calculation of the indicator based on weighted average arithmetic values of properties
3. Calculation based on weighted geometric properties
A comprehensive assessment of the quality level involves the use of
The development of complex indicators of sets of properties. This is
Tod is used in cases where it is necessary to most accurately assess
quality of complex products. The need for the "convolution" of all
indicators of properties in order to obtain one complex
indicator is determined by practical feasibility.
Comprehensive indicator of the combination of properties of K depends
from the "weighted" parameters of the properties taken into account
ki i. from indicators of individual properties, taking into account their weight, significance
for K. Therefore, K = f ( k i), where
ki is a quantity characterizing the size of the i -th property, taking into account its significance;
i = 1, 2, 3, ..., p ; where n is the total number of properties taken into account.
Requirements for an integrated indicator
qualities are:
1) representativeness - the representation in it of all the
new product characteristics, by which its
honor;
2) the monotony of changes in the complex indicator
the quality of the product when changing any of the single indicators
quality at fixed values of other indicators;
3) criticality (sensitivity) to varying para-
meters. This requirement is that the integrated display
The quality manager must respond in a coordinated manner to changes in each
from individual indicators. Comprehensive indicator is
the function of evaluating all indicators of properties, and its sensitivity
determined by the first derivative of this function. Value com
plex indicator should be especially sensitive in those
In cases where a single indicator goes beyond
allowable limits. At the same time, a comprehensive quality indicator
should significantly reduce its numerical value;
4) normalization - the numerical value of the complex
the indicator concluded between the greatest and least significant
relative quality indicators. This requirement
normalization determines the scale of the scale
rhenium complex indicator;
5) comparability
(comparability) of the results
full quality assessment is ensured by the uniformity of
Dov their calculations, in which indicators of the properties should be
razheny in dimensionless quantities.
Conversion of natural dimensions to dimensionless (reduced
d) units of measurement is carried out by appropriately
conversion.
For example, a linear dependence of the form is often used:
q = wx P,
where q is the value of the indicator in dimensionless numbers, in points or parts;
P - value of the indicator in physical units;
w is the conversion factor.
The use of linear dependence simplifies the conversion
single indicator, expressed in natural units
measurements in a dimensionless measure. However, in a number of cases
Tea needs to accept non-linear function dependency
q = f ( P )
. The formula for this relationship is derived from
or observing the nature of the change in P.
The level of product quality, determined by the complex
method is the ratio of the complex indicator
the properties of the estimated object (Kotz) to the corresponding indicator of the base sample ( K ots
bases), i.e .: Yk = Kotz / Kbaz
Comprehensive indicator of the combination of different properties
K must take into account the significance (weight) of each of them, i.e.
take into account the degree of influence of the values of individual properties on the final
indicator
(level) quality. Quantitative characteristic
The significance of this indicator among other indicators is
weight coefficient. When finding the value of the complex
value of the aggregate characteristics of the properties necessary
parameter value of each of the many properties of "weigh",
those. multiply by the appropriate weight coefficient.
With a comprehensive method of quality assessment determine
the so-called weighted average of the aggregates of all
taken into account properties.
If the values of the properties taken into account are proportional to the influence
on the final quantitative assessment of quality, then the value of K
find as a weighted average arithmetic by the formula:
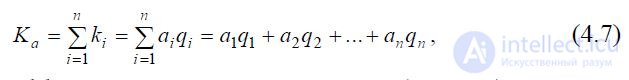
Where
ai is the weight coefficient of the i- th parameter (property);
qi is the dimensionless quantity of the ith property;
n - the number of considered properties.
The quality level of the estimated object, determined by the weighted arithmetic indices of the aggregates
The properties of Ka.oc and Ka.oc are:
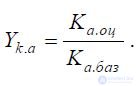
Another formula for calculating Yk.a is also known:
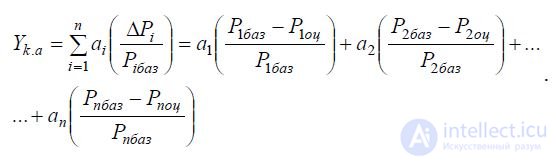
Subject to restrictions on the limiting values
properties, and considering their importance, it is recommended that
read the weighted arithmetic values of such properties
according to the formulas:
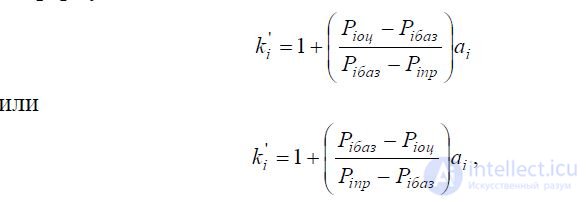
Where
P iпр - the limiting value of the parameter of the i -th property;
ai is the weight coefficient of the i -th property.
If all indicators of properties have limitations
on their limiting values, the assessment (level) of the quality of the object
find the weighted average of the arithmetic values of aggregate indicators of properties as
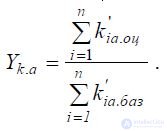
Another way to find a quantitative assessment of the quality
complex method is that initially
find the relative values of the levels of all units considered
individual and generalized indicators of properties (if there is a generalized
indicators of property groups), that is, calculate Yi ( i = 1, 2, 3 .... n properties). Knowing the meanings of all
Yi, find the corresponding values of Yk, i.e. Y.a. or Ykg
Consequently, a comprehensive indicator of the level of quality
determined by weighted average arithmetic values
separate levels of properties, calculated by the formula:
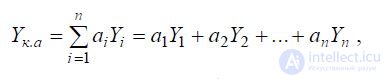
Where
ai is the weight coefficient of the i -th index of the level of the corresponding properties;
Yi is a relative indicator of the i -th property of the evaluated and base objects (samples).
If the influence of the properties taken into account on the value of K
non-linear, power dependence, then calculate
weighted average of these properties
formula:
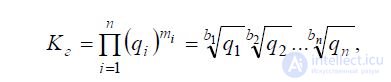
where m i = 1 / b - weight coefficient;
 - the number of evaluated quality indicators;
- the number of evaluated quality indicators;
bi is the denominator of the number of the i -th weight index (degree, root);
qi is the dimensionless (reduced by the conversion coefficient w ) value of the parameter of the i -th property;
n - the number of considered properties.
The calculation of the level of quality for "geometrically weighted"
indicators of sets of properties carried out according to the formula:
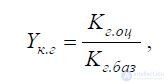
Where
Kgc - geometric index of the evaluated sample;
Kg base is the geometric index of the base sample.
Weighted average geometric complex display
the body of quality (quality level) is calculated by the formula:
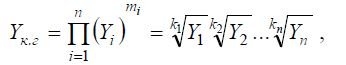
Where
mi is the weight coefficient of the i- th property;
ki is the denominator of the number of the i -th weight index (degree, root);
Yi- level of property i ;
n - the number of considered properties.
Comments
To leave a comment
Qualimetry reliability and quality
Terms: Qualimetry reliability and quality