Lecture
Let the function y = f ( x ) ≥ 0 be continuous (and therefore integrable) on the segment [ a, b ] (Fig. 13). The integral sum S n with f ( x ) ≥ 0 is equal to the area of the figure composed of rectangles with sides f (ξ i ) · h i . Consequently, the limit of the sequence S n as h → 0 is equal to the area S of the curvilinear trapezium, i.e. figures bounded by the line y = f ( x ) , axis OX and straight lines x = a, x = b : 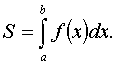
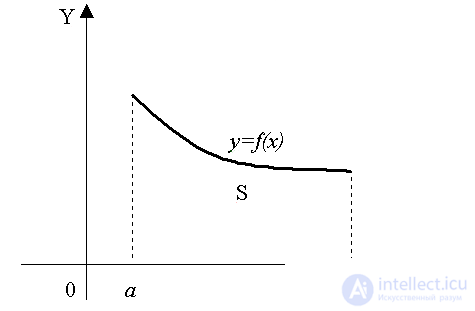
Fig. 13
Comments
To leave a comment
Mathematical analysis. Integral calculus
Terms: Mathematical analysis. Integral calculus