Lecture
Example N 1
Find the indefinite integral:
Decision.
Answer:
Example N 2
Find the indefinite integral:
Decision.
Answer:
Example N 3
Find the indefinite integral:
.
Decision.
To integrate this function, it is necessary to make a change of variable 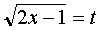 .
.
We got the wrong fraction. Select the integer part in it, dividing the polynomial standing in the numerator by the denominator polynomial by a corner.
Answer:
Example N 4
Find the indefinite integral:
Decision.
We got an irregular fraction; we single out the integer part in it, dividing the polynomial in the numerator into a denominator polynomial by a corner:
Answer:
Example N 5
Find the indefinite integral:
Decision.
Answer:
Example N 6
Find the indefinite integral:
Decision.
Answer:
Example N 7
Find the area of the figure bounded by the lines:
Decision.We construct a figure on the OXY plane bounded by y 1 = 4 - x 2 - by a parabola and y 2 = 2 - x - by a straight line (Fig. 16).
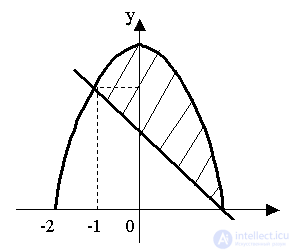
Fig. sixteen
Find the intersection points of the functions y 1 and y 2 :
Since 4 - x 2 ≤ 2 - x on the segment [-1; 2], the area S of this figure is calculated as follows:
The answer is 4.5 .
Example N 8
Find the length of the arc curve 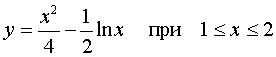 .
.
Decision.
Answer: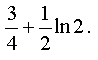
Example N 9
Find the length of the arc curve 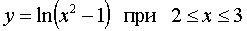 .
.
Decision.
The arc is explicitly specified. 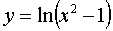 , the limits of integration are given 2 ≤ x ≤ 3, we make the integral
, the limits of integration are given 2 ≤ x ≤ 3, we make the integral
Answer: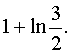
Example N 10
Find the length of the astroid arc
.
Decision.
The curve is set parametrically, therefore, its length L is calculated as follows:
The answer is: 4.5
Example N 11
Find the volume of the body obtained by rotating around the OX axis of the figure, which is limited by parabolas y = 3 - x 2 , y = x 2 + 1.
Decision.
We construct a figure on the plane of the OXU , bounded by parabolas y = 3 - x 2 , y = x 2 + 1 (Fig. 17).
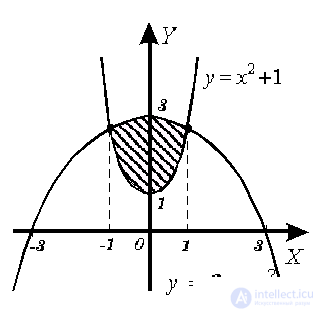
Fig. 17
Find the intersection points of the curves:
.
Then
Answer: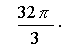
Example N 12
Change the order of integration:
Decision.
We build the integration domain D , which consists of two areas - D 1 and D 2 (Fig. 18):
Area D 1 is bounded by a semicircle 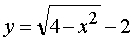 and straight lines y = 0, x = 2.
and straight lines y = 0, x = 2.
The domain D 2 is bounded by the straight lines y = x - 4, y = 0, x = 2.
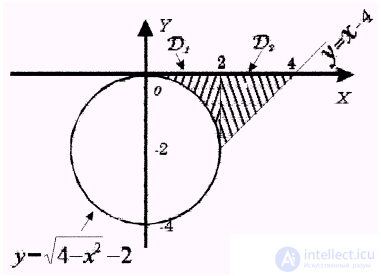
Fig. 18
Region D is correct in the direction of the axis of the shelter . The largest value of y in the domain D is the number y = 0, and the smallest y = -2. From the equation 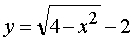 Express x through y :
Express x through y :
Function 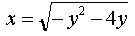 sets the left boundary of the domain D. From the equation y = x - 4 we express x through y : x = y + 4. The function x = y + 4 sets the right boundary of the domain D. Therefore, the domain D is given by the inequalities:
sets the left boundary of the domain D. From the equation y = x - 4 we express x through y : x = y + 4. The function x = y + 4 sets the right boundary of the domain D. Therefore, the domain D is given by the inequalities: 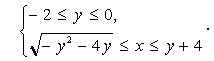
Now we change the order of integration in the double integral:
Answer:
Example N 13
Find the area of the figure bounded by lines 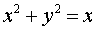 ,
, 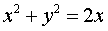 ,
, 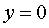 ,
, 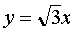 .
.
Decision.
Let's build a shape D bounded by given lines (fig. 19):
- circle centered at a point
radius
;
- a circle with a center at the point (1; 0), radius 1;
- OX axis;
- straight with the slope
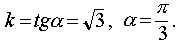
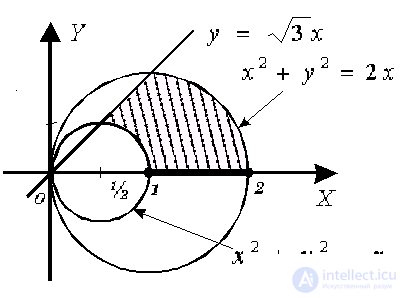
Fig. nineteen
Expressing circles in polar coordinates:
we conclude that the domain D can be given by the inequalities: 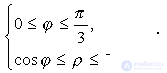
Find the area S of the area D according to the formula of the area of the figures in polar coordinates:
Answer: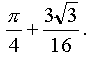
Example N 14
Calculate the volume of the body bounded by the surfaces 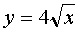 ,
, 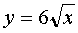 ,
, 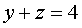 ,
, 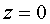 .
.
Decision.
The body is bounded by parabolic cylinders, which form parallel to the axis OZ : 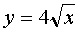 ,
, 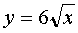 ; coordinate plane
; coordinate plane 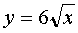 ; and the plane z = 4 - y . Let us depict the body (Fig. 20) and its projection (Fig. 21) in the DCS plane in the figures .
; and the plane z = 4 - y . Let us depict the body (Fig. 20) and its projection (Fig. 21) in the DCS plane in the figures .
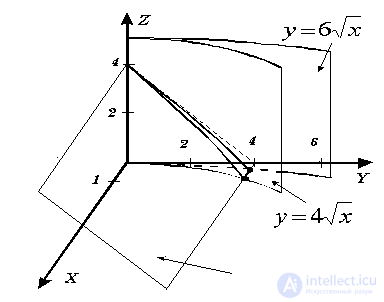 | 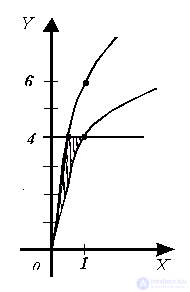 |
| Fig. 20 | Fig. 21 |
The basis of a given body is the domain D , given by the inequalities: 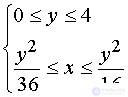 .
.
Find the volume V of the body using a double integral:
First we find the inner integral:
Then we find the external integral:
Answer: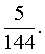
Comments
To leave a comment
Mathematical analysis. Integral calculus
Terms: Mathematical analysis. Integral calculus