Lecture
Let the function f ( x, y ) be defined inside some domain D and on its boundary. Divide the domain D into n partial domains D 1 , D 2 , ..., D n . We denote their areas by σ 1 , σ 2 , ..., σ n . The largest chord (the segment connecting the two points of the boundary of the region) of each of the regions is called its diameter. Let h denote the diameter, the largest of all n diameters. In each partial region, we take the point ( P 1 ( x 1 ; y 1 ) in the region D 1 , P 2 ( x 2 ; y 2 ) in the region D 2 , etc.). We make the integral sum:
Let n tend to infinity so that h tends to zero.
The final limit of the sequence S n (if it exists) as h → 0 , which depends neither on the method of dividing the domain D , nor on the choice of the points P 1 , P 2 , ..., P n , is called the double integral of the function f ( x, y ) and is denoted by 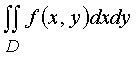 .
.
The function f ( x, y ) is called an integrable function on the domain D. The region D is called the region of integration .
A continuous function on a closed domain is integrable on this domain.
Comments
To leave a comment
Mathematical analysis. Integral calculus
Terms: Mathematical analysis. Integral calculus