Lecture
Integrals with infinite limits and integrals of functions with infinite discontinuities on the integration interval are called improper integrals .
The improper integral of the function y = f ( x ) in the range from a to + ∞ is determined by the equality 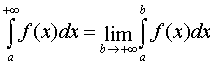 .
.
If this limit exists and is finite, then the improper integral converges; if the limit does not exist (or is equal to infinity), then the improper integral diverges .
Similarly, the following improper integrals are calculated:
If the function y = f ( x ) has an infinite discontinuity at the point 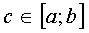 and continuous for a ≤ x <c and c <x ≤ b , then
and continuous for a ≤ x <c and c <x ≤ b , then 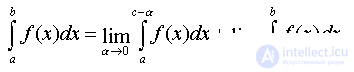 .
.
The improper integral of a function that has an infinite discontinuity on the integration interval is called convergent if both limits exist: 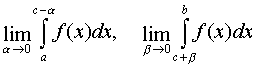 and divergent if at least one of these limits does not exist (or is equal to infinity).
and divergent if at least one of these limits does not exist (or is equal to infinity).
Comments
To leave a comment
Mathematical analysis. Integral calculus
Terms: Mathematical analysis. Integral calculus