Lecture
At the stage of research and design of systems for constructing and implementing machine models (analytical and simulation), the statistical test method (Monte-Carlo) is widely used, which is based on the use of random numbers, that is, possible values of a certain random variable with a given probability distribution. Statistical modeling is a method of computer-generated statistical data on the processes occurring in the system being modeled. To obtain estimates of interest for the characteristics of the simulated system S, taking into account the effects of the external environment E, statistical data are processed and classified using the methods of mathematical statistics.
The essence of the method of statistical modeling. Thus, the essence of the method of statistical modeling is reduced to the construction for the process of functioning of the system under study S of a certain modeling algorithm that simulates the behavior and interaction of elements of the system, taking into account the random
input effects and effects of the external environment E, and the implementation of this algorithm using software and hardware of a computer.
There are two areas of application of the method of statistical modeling :
1) to study stochastic systems;
2) to solve deterministic problems.
The main idea, which is used to solve deterministic problems by statistical modeling, is to replace a deterministic problem with an equivalent circuit of a certain stochastic system, the output characteristics of the latter coincide with the result of solving a deterministic problem. Naturally, with such a replacement, instead of an exact solution of the problem, an approximate solution is obtained and the error decreases with increasing number of tests (realizations of the modeling algorithm) N.
As a result of the statistical modeling of the system S, a series of particular values of the unknown quantities or functions are obtained, the statistical processing of which makes it possible to obtain information about the behavior of a real object or process at arbitrary points in time. If the number of realizations N is sufficiently large, then the results of modeling the system acquire statistical stability and with sufficient accuracy can be taken as estimates of the desired characteristics of the process of functioning of the system S.
An example of a deterministic problem is the problem of calculating a one-dimensional or multidimensional integral by the method of statistical tests.
The theoretical basis of the method of statistical modeling of computer systems is the limit theorems of probability theory. The sets of random phenomena (events, magnitudes) obey certain regularities, allowing not only to predict their behavior, but also to quantify some of their average characteristics, which show a certain stability. Characteristic patterns are also observed in the distributions of random variables, which are formed by adding up a multitude of effects. The expression of these regularities and stability of the average indicators are the so-called limit theorems of the theory of probability, some of which are given below in a formulation suitable for practical use in statistical modeling. The fundamental value of limit theorems is that they guarantee high quality of statistical estimates with a very large number of tests (implementations) N. Practically acceptable quantitative estimates of system characteristics in statistical modeling can often be obtained with relatively small (using a computer) N.
1. Chebyshev inequality .
For non-negative function 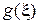 random variable
random variable 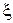 and any K> 0 inequality holds
and any K> 0 inequality holds
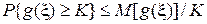
In particular, if 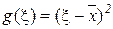 and
and 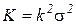 (Where
(Where 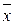 - average;
- average; 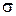 - standard deviation),
- standard deviation),
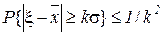 .
.
2. Bernoulli's theorem. If N independent tests are carried out, in each of which some event A is carried out with probability p , then the relative frequency of occurrence of the event m / N at 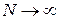 converges in probability to p , that is, for any
converges in probability to p , that is, for any 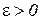
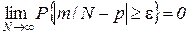 ,
,
where m is the number of positive test outcomes.
3. The Poisson theorem. If N independent tests are carried out and the probability of the occurrence of event A in the i- th test is equal to 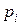 , then the relative frequency of occurrence of the event m / N at
, then the relative frequency of occurrence of the event m / N at 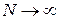 converges in probability to the average of the probabilities
converges in probability to the average of the probabilities 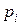 i.e. for any
i.e. for any 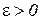
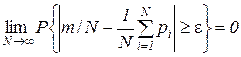 .
.
4. Chebyshev theorem . If the N independent tests are observed values 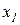 , ...,
, ..., 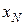 random variable
random variable 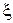 then at
then at 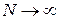 the arithmetic mean of the values of a random variable converges in probability to its expectation a, i.e. for any
the arithmetic mean of the values of a random variable converges in probability to its expectation a, i.e. for any 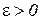
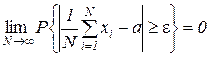 .
.
5. The generalized Chebyshev theorem. If a 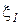 , ...,
, ..., 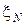 - independent random variables with mathematical expectations
- independent random variables with mathematical expectations 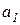 , ...,
, ..., 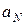 and dispersions
and dispersions 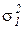 , ...,
, ..., 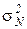 bounded above by the same number, then
bounded above by the same number, then 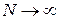 the arithmetic mean of the values of a random variable converges in probability to the arithmetic mean of them
the arithmetic mean of the values of a random variable converges in probability to the arithmetic mean of them
mathematical expectation:
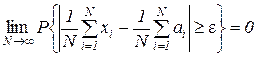 (*)
(*)
6. Markov's theorem . The expression (*) is also valid for dependent random variables. 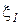 , ...,
, ..., 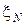 , If only
, If only
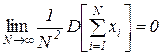 .
.
The set of theorems establishing the stability of averages is usually called the law of large numbers.
7. Central limit theorem . If a 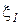 , ...,
, ..., 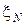 - independent identically distributed random variables having expectation a and variance
- independent identically distributed random variables having expectation a and variance 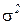 then at
then at 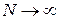 amount distribution law
amount distribution law 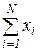 unlimited approaches to normal:
unlimited approaches to normal:
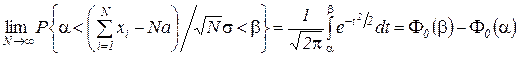 .
.
Here is the probability integral
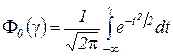 .
.
8. Laplace theorem. If in each of the N independent trials event A appears with probability p , then
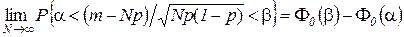
where m is the number of occurrences of event A in N trials. The Laplace theorem is a special case of the central limit theorem.
Comments
To leave a comment
Theory of Reliability
Terms: Theory of Reliability