INDICATORS OF RELIABILITY OF NON-REPAIRED OBJECTS

Such objects work until the first failure. For assessing the reliability of such objects, the probabilistic characteristics of a random variable — time to failure T are used. By time, we understand the duration or amount of work of an object, measured in hours, kilometers, cycles, etc.

A complete characteristic of any random variable is its distribution law, i.e. the relationship between the possible values ​​of a random variable and the probabilities corresponding to these values.

Reliability indicators include:

reliability function p (t);

distribution density of up to failure time f (t);

failure rate l (t).

The reliability function is a function that expresses the probability that T — a random time between failures of objects — will be more than a given time (0, t), counted from the start of operation, i.e.

p (t) = P {Tіt}.

Here are some obvious properties of p (t):

1) p (0) = 1, i.e. you can consider the trouble-free operation of only those objects that were operational at the time of inclusion;

2) p (t) is a monotonically decreasing function of a given operating time t;

3) p (t) ®0 with t® + Ґ, i.e. any object over time will fail.

Along with p (t), the unreliability function is used.

q (t) = 1-p (t) = P {T <t}.

It characterizes the probability of failure of an object in the interval (0, t). The unreliability function is a distribution function of a random variable T; this function is sometimes denoted F (t).

Fig.1.2. The reliability functions p (t) and unreliability q (t) of the object.

In many tasks, the probability of failure-free operation is used as an indicator of reliability — the probability that no object fails to occur within a given operating time. In this case, the conditional probability p (t ₁ , t ₂ ) of trouble-free operation during the operating time from t ₁ to t ₂ is usually meant, provided that at t _{1 the} object was operational. This conditional probability can be determined by the reliability function.

Consider two intervals (0, t ₁ ) and (t ₁ , t ₂ ). The event, consisting in trouble-free operation during the interval (0, t ₂ ), is a combination of two events:

1) the object worked smoothly on the interval (0, t ₁ );

2) remaining operable by the time t _{1, the} object worked smoothly on the interval (t ₁ , t ₂ ).

Therefore, according to the multiplication rule

p (t ₂ ) = p (t ₁ ) p (t ₁ , t ₂ ),

Consequently,

p (t ₁ , t ₂ ) = p (t ₂ ) / p (t ₁ ) (1.1)

Thus, the conditional probability of failure-free operation on the interval (t ₁ , t ₂ ) is equal to the ratio of the values ​​of the reliability function at the beginning and end of the interval.

For small time intervals, the values ​​of p (t ₁ , t ₂ ) will be close to unity. Therefore, along with p (t), other indicators of reliability are used, for example, the density of the distribution of time to failure

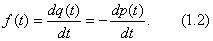
The density of distribution of time to failure f (t) is the differential form of the law of time distribution to failure. The density f (t) is a non-negative function, with

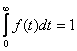
In accordance with (1.2), the reliability function and the unreliability function are related to f (t) by the relations

The value f (t) dt characterizes the probability of failure for the interval of operation (t, t + dt) of an object taken at random from a set of identical objects. It is not known whether this object is operational at the beginning of the interval (i.e. at time t) or has failed before. This is not always convenient; therefore, in practice, the failure rate l (t) is often used — the conditional probability density for the failure of an unrepairable object, provided that no failure has occurred before this time.

The conditional probability of failure of an object during the operating time (t, t + dt) under the assumption of its trouble-free operation until time t is usually expressed by the formula

z = l (t) dt,

failed objects are excluded from consideration at time t.

And

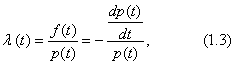
Solving equation (1.3) with the initial condition p (0) = 1 gives the formula for the reliability function

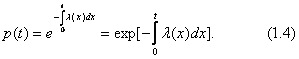
When l = const, formula (1.4) is significantly simplified:

p (t) = exp (-lt). (1.5)

As indicators of the reliability of non-repairable products, the numerical characteristics of random operating time to failure are also used. They are usually easier to determine from experimental data than p (t), l (t), f (t). The most frequently used mean time to failure (expected value of time to failure).

According to the definition of the mathematical expectation of a continuous non-negative random variable, by performing some transformations we obtain the average time to failure

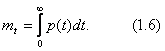
When l = const we have:

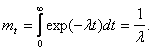
Substituting the value t = m _t = 1 / l into (1.5), we obtain that when l = const, the mean time to failure can be understood as the time t = m _t , during which the object remains operable with probability p (m _t ) = exp (-1) "0.37

The values ​​of m _t are usually calculated by experimental

data on failures of elements in the initial period of their operation.

In practice, two conditional averages are of interest.

operating time of non-repairable objects:

1) average useful life 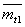provided that when

the achievement of operating time t ₁ all remaining workable

facilities are being decommissioned;

2) the average duration of the work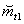

provided that the object worked smoothly on the interval

(0, t ₁ )

And m _t = 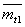+ 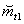p (t ₁ ).

When l = const we have: 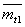= m _t [1-exp (-lt ₁ )];

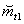= m _t = 1 / l.

This ratio is illustrated in Figure 1.1.