Content
Introduction
Recurrent relations for the calculation of a fixed spectral reference signal
Hörzel Algorithm
An example of the use of the algorithm of Goertzel
findings
Introduction
Earlier we considered the discrete Fourier transform (DFT) and its properties, as well as fast Fourier transform algorithms (FFT). We found that the FFT algorithms can significantly save computational resources when calculating the DFT. However, it is often necessary to calculate not the entire DFT, but only a fixed number of spectral samples. For example, such a task arises when decoding DTMF signals. In this case, the use of FFT algorithms may not be effective, since in order to obtain a single spectral reference, it will be necessary to calculate the entire DFT.
In this article, we will consider the Goetzel algorithm for calculating the discrete Fourier transform, which has found wide application in decoding DTMF signals. This algorithm allows you to effectively calculate the fixed spectral DFT samples without the need to calculate all the DFTs. As will be shown below, the Goetzel algorithm is a DFT implementation in the form of an IIR filter, which simplifies its hardware implementation.
Recurrence ratio for calculating a fixed spectral sample of the signal
Expression for discrete
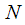
- point Fourier transform of the signal
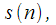
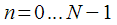
has the form:
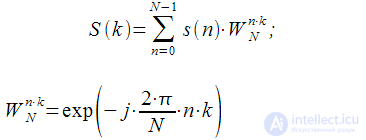 | (one) |
Turn factors
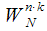
have the following property:
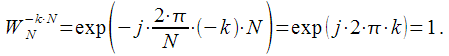 | (2) |
Thus, multiplying the expression (1) by
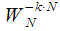
does not change the result:
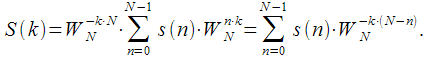 | (3) |
We write the amount (3):
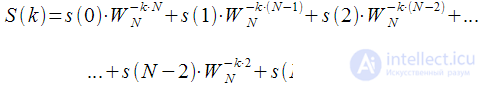 | (four) |
Denote
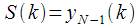
for a fixed number of spectral reference
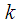
besides, we put in (4)
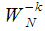
for brackets and get:
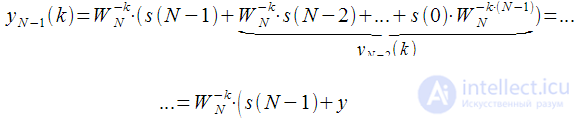 | (five) |
Inside the brackets in expression (5) can be identified
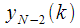
in which you can also endure
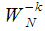
for brackets:
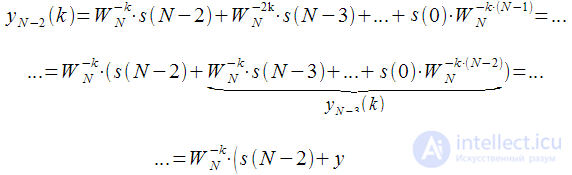 | (6) |
Now got what
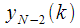
can be obtained through
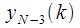
in which you can again
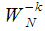
take out the brackets. Thus, we have obtained a recurrent relation for calculating
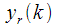
at any step
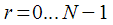
through
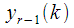
obtained in the previous step for a fixed number of spectral reference
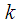
:
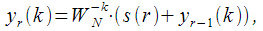 | (7) |
Where
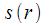
- counting the input signal with the number
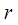
. This recurrence relation in step number
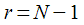
leads us to
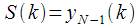
i.e. on
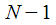
step, we get the spectral count with the number
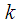
. After analyzing (7), it can be noted that the recurrence relation can be interpreted as a difference equation of an IIR filter with a complex coefficient
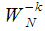
The structural diagram of which is shown in Figure 1.
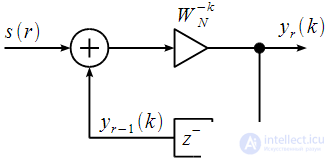
Figure 1: Block diagram of an IIR filter that implements the calculation of the spectral count with number k
Denoting by
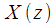
and
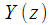
z - images
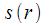
and
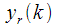
accordingly, the expression (7) can be represented as:
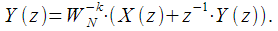 | (eight) |
From (8) you can get the transfer characteristic of the IIR filter
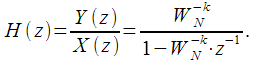 | (9) |
Now is the time to analyze what all the previous arguments have led us to.
Let me remind you that we fixed the number of the spectral reference
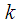
and transformed the DFT expression for one fixed spectral reference to the recurrence relation, which allows us to
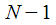
step to get the value of the desired
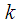
th spectral reference
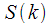
. In this case, all intermediate values of the recurrence relation
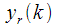
we are not interested, but only interested
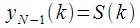
. This is important and will be useful to us in the future. Then we treated the recurrence relation as a difference IIR filter equation with a transfer characteristic (9). As a result, we received a “sophisticated filter” with a complex coefficient
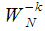
whose application on
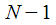
-th iteration at the output gives
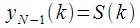
. With fixed
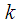
value of the complex coefficient
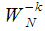
always on.
Hörzel Algorithm
To calculate a single spectral reference
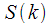
when using IIR filter required
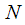
complex multiplications and additions, which does not give any advantages in comparison with the DFT calculation "in the forehead" according to expression (1).
However, the reduction of calculations can be obtained by multiplying the numerator and denominator of the transfer characteristic IIR filter (9) by
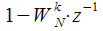
:
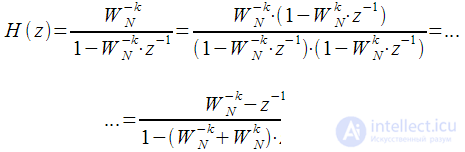 | (ten) |
Consider in more detail the amount:
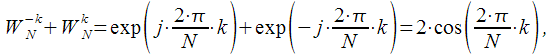 | (eleven) |
then (10) taking into account (11) we can write down:
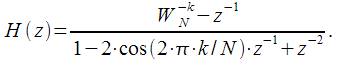 | (12) |
The block diagram of the IIR - filter of the second order corresponding to (12) is shown in Figure 2 (the block diagrams of the IIR filters were discussed in detail here), where
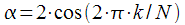
.
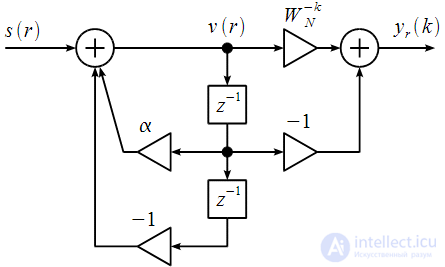
Figure 2: IIR block diagram - 2nd order filter
Note that
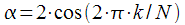
- the real coefficient, respectively, of the multiplication in the recursive branch of the filter became real, and multiplication by -1 can be ignored. We have one complex coefficient left
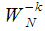
in the numerator of the transfer characteristic. But we found that intermediate values
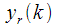
we are not important, respectively multiplied by
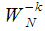
can only be on
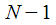
iterations when calculated directly
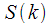
because of intermediate values
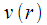
it will not affect in any way. Thus, applying a second order filter allows you to calculate
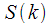
for fixed
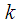
using
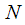
multiplications, but not complex, but real, which leads to a reduction of calculations by 2 times (one complex multiplication requires two real ones), plus one complex multiplication by
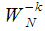
on the last iteration when calculating directly
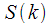
.
Based on Figure 2, the spectral count
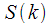
equals:
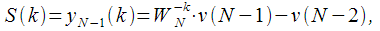 | (13) |
Where
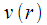
- intermediate values (see figure 2), which are calculated iteratively:
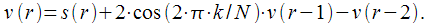 | (14) |
Thus, the algorithm is reduced to an iterative calculation.
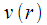
according to (14), after which the last two values
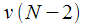
and
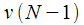
used to calculate the spectral reference
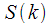
.
An example of the use of the algorithm of Goertzel
Let be
source signal
shown in Figure 3.
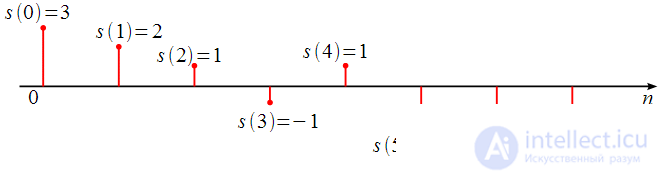
Figure 3: Source Signal
Calculate with the help of the algorithm of Goertzel spectral reading
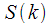
with number

. Pre-calculate the coefficient
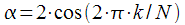
and
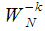
:
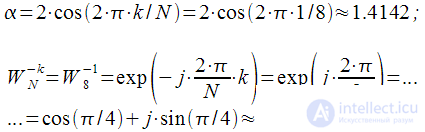 | (15) |
As the initial conditions for the calculation, we specify:
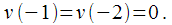 | (sixteen) |
Make an iterative calculation
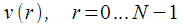
according to (14):
 | (17) |
Then, according to expression (13), you can get the values for the spectral reference:
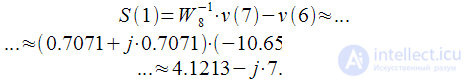 | (18) |
You can independently verify that the value obtained
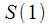
fully consistent with the result of the DFT.
Below is the source code of the program in the C language, which calculates the spectral reference.
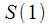
according to the considered example.
#include <stdio.h>
#include <stdlib.h>
#define _USE_MATH_DEFINES
#include <math.h>
int main () {
// initial data
int N = 8; // points DFT
int k = 1; // number of spectral count
// source signal
double s [8] = {3, 2, 1, -1, 1, -2, -3, -2};
// array of intermediate results
double v [8] = {0, 0, 0, 0, 0, 0, 0, 0};
// alpha parameter
double a = 2 * cos (2 * M_PI * k / N);
// swivel set W_N ^ -k
double wr = cos (2 * M_PI * k / N); // real part
double wi = sin (2 * M_PI * k / N); // imaginary part
// account v [-1] = v [-2] = 0
v [0] = s [0];
v [1] = s [1] + a * v [0];
// iterative calculation of the array v according to (14)
for (int i = 2; i <n; i ++)
v [i] = s [i] + a * v [i-1] - v [i-2];
// real and imaginary parts of the spectral reading S (1) according to (13)
double SR = v [N-1] * wr-v [N-2];
double SI = v [N-1] * wi;
// print the result
printf ("S (% d) =% .4f% +. 4fj \ n", k, SR, SI);
system ("Pause");
return 0;
}
findings
The filter shown in Figure 2 implements the calculation of the spectral count with the number
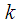
. To implement the calculation of all
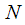
spectral samples, you must put in parallel
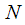
such filters. The advantage of the Herzler algorithm is that each spectral sample is calculated independently of the others, and you do not need to count all the DFTs for several samples. This is widely used for decoding DTMF signals when analyzing the amplitude of several harmonics of a signal. But the Gozel algorithm also has a flaw. To calculate a single spectral reference is required
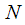
iterations, with intermediate values
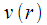
, except for the last two, do not carry useful information, but they have to count. The Goertz Algorithm is not attractive for the calculation of all spectral samples of the DFT due to its high computational complexity. The fast Fourier transform algorithms are much better suited for calculating the “full” DFT.
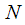 - point Fourier transform of the signal
- point Fourier transform of the signal 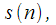
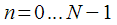 has the form:
has the form: 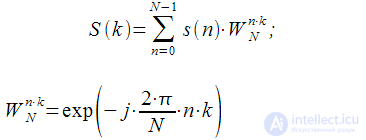
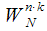 have the following property:
have the following property: 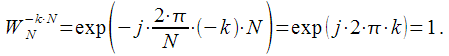
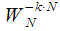 does not change the result:
does not change the result: 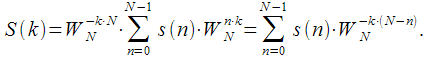
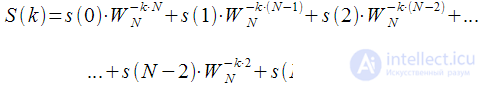
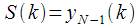 for a fixed number of spectral reference
for a fixed number of spectral reference 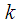 besides, we put in (4)
besides, we put in (4) 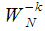 for brackets and get:
for brackets and get: 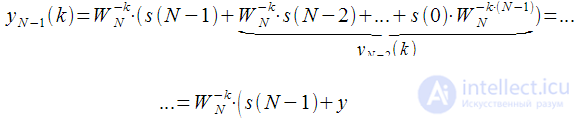
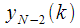 in which you can also endure
in which you can also endure 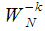 for brackets:
for brackets: 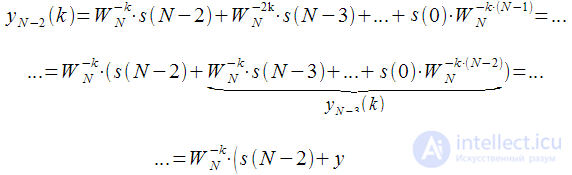
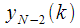 can be obtained through
can be obtained through 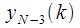 in which you can again
in which you can again 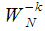 take out the brackets. Thus, we have obtained a recurrent relation for calculating
take out the brackets. Thus, we have obtained a recurrent relation for calculating 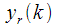 at any step
at any step 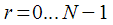 through
through 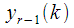 obtained in the previous step for a fixed number of spectral reference
obtained in the previous step for a fixed number of spectral reference 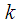 :
: 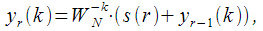
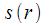 - counting the input signal with the number
- counting the input signal with the number 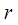 . This recurrence relation in step number
. This recurrence relation in step number 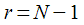 leads us to
leads us to 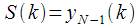 i.e. on
i.e. on 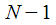 step, we get the spectral count with the number
step, we get the spectral count with the number 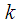 . After analyzing (7), it can be noted that the recurrence relation can be interpreted as a difference equation of an IIR filter with a complex coefficient
. After analyzing (7), it can be noted that the recurrence relation can be interpreted as a difference equation of an IIR filter with a complex coefficient 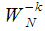 The structural diagram of which is shown in Figure 1.
The structural diagram of which is shown in Figure 1. 
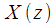 and
and 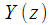 z - images
z - images 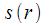 and
and 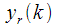 accordingly, the expression (7) can be represented as:
accordingly, the expression (7) can be represented as: 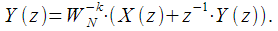
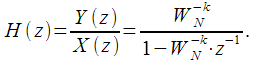
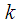 and transformed the DFT expression for one fixed spectral reference to the recurrence relation, which allows us to
and transformed the DFT expression for one fixed spectral reference to the recurrence relation, which allows us to 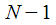 step to get the value of the desired
step to get the value of the desired 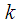 th spectral reference
th spectral reference 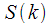 . In this case, all intermediate values of the recurrence relation
. In this case, all intermediate values of the recurrence relation 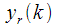 we are not interested, but only interested
we are not interested, but only interested 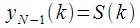 . This is important and will be useful to us in the future. Then we treated the recurrence relation as a difference IIR filter equation with a transfer characteristic (9). As a result, we received a “sophisticated filter” with a complex coefficient
. This is important and will be useful to us in the future. Then we treated the recurrence relation as a difference IIR filter equation with a transfer characteristic (9). As a result, we received a “sophisticated filter” with a complex coefficient 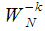 whose application on
whose application on 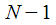 -th iteration at the output gives
-th iteration at the output gives 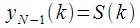 . With fixed
. With fixed 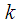 value of the complex coefficient
value of the complex coefficient 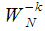 always on.
always on. 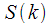 when using IIR filter required
when using IIR filter required 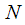 complex multiplications and additions, which does not give any advantages in comparison with the DFT calculation "in the forehead" according to expression (1).
complex multiplications and additions, which does not give any advantages in comparison with the DFT calculation "in the forehead" according to expression (1). 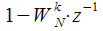 :
: 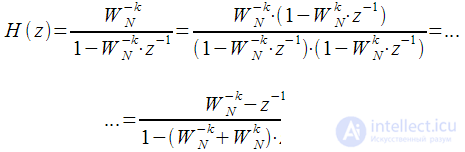
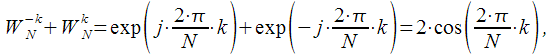
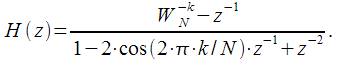
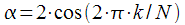 .
. 
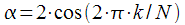 - the real coefficient, respectively, of the multiplication in the recursive branch of the filter became real, and multiplication by -1 can be ignored. We have one complex coefficient left
- the real coefficient, respectively, of the multiplication in the recursive branch of the filter became real, and multiplication by -1 can be ignored. We have one complex coefficient left 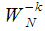 in the numerator of the transfer characteristic. But we found that intermediate values
in the numerator of the transfer characteristic. But we found that intermediate values 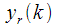 we are not important, respectively multiplied by
we are not important, respectively multiplied by 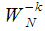 can only be on
can only be on 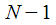 iterations when calculated directly
iterations when calculated directly 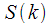 because of intermediate values
because of intermediate values 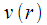 it will not affect in any way. Thus, applying a second order filter allows you to calculate
it will not affect in any way. Thus, applying a second order filter allows you to calculate 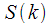 for fixed
for fixed 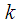 using
using 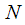 multiplications, but not complex, but real, which leads to a reduction of calculations by 2 times (one complex multiplication requires two real ones), plus one complex multiplication by
multiplications, but not complex, but real, which leads to a reduction of calculations by 2 times (one complex multiplication requires two real ones), plus one complex multiplication by 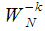 on the last iteration when calculating directly
on the last iteration when calculating directly 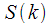 .
.  equals:
equals: 
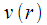 - intermediate values (see figure 2), which are calculated iteratively:
- intermediate values (see figure 2), which are calculated iteratively: 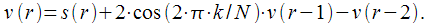
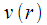 according to (14), after which the last two values
according to (14), after which the last two values 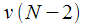 and
and 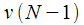 used to calculate the spectral reference
used to calculate the spectral reference 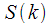 .
.  source signal
source signal  shown in Figure 3.
shown in Figure 3. 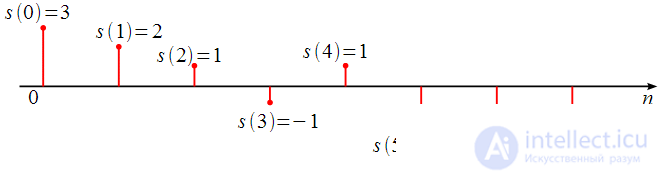
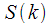 with number
with number  . Pre-calculate the coefficient
. Pre-calculate the coefficient 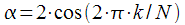 and
and 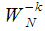 :
: 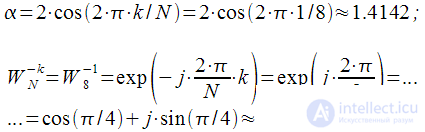
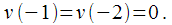
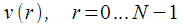 according to (14):
according to (14): 
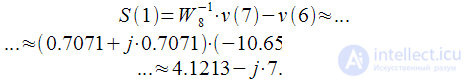
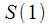 fully consistent with the result of the DFT.
fully consistent with the result of the DFT. 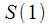 according to the considered example.
according to the considered example. 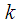 . To implement the calculation of all
. To implement the calculation of all 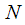 spectral samples, you must put in parallel
spectral samples, you must put in parallel 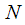 such filters. The advantage of the Herzler algorithm is that each spectral sample is calculated independently of the others, and you do not need to count all the DFTs for several samples. This is widely used for decoding DTMF signals when analyzing the amplitude of several harmonics of a signal. But the Gozel algorithm also has a flaw. To calculate a single spectral reference is required
such filters. The advantage of the Herzler algorithm is that each spectral sample is calculated independently of the others, and you do not need to count all the DFTs for several samples. This is widely used for decoding DTMF signals when analyzing the amplitude of several harmonics of a signal. But the Gozel algorithm also has a flaw. To calculate a single spectral reference is required 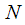 iterations, with intermediate values
iterations, with intermediate values 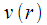 , except for the last two, do not carry useful information, but they have to count. The Goertz Algorithm is not attractive for the calculation of all spectral samples of the DFT due to its high computational complexity. The fast Fourier transform algorithms are much better suited for calculating the “full” DFT.
, except for the last two, do not carry useful information, but they have to count. The Goertz Algorithm is not attractive for the calculation of all spectral samples of the DFT due to its high computational complexity. The fast Fourier transform algorithms are much better suited for calculating the “full” DFT.
Comments
To leave a comment
Digital signal processing
Terms: Digital signal processing