Lecture
Accounting for uncertain factors, the distribution law of which is unknown, is based on the formation of special criteria on the basis of which decisions are made - the criteria of Wald, Savage, Hurwitz and Bayes-Laplace.
The model of a problem situation is:
< U, V, W >,
where U = { u i } is the set of strategies (solutions), 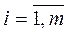 ;
;
V = { v j } is the set of states of nature, 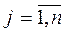 ;
;
W = | w ij | - the decision matrix, the matrix element w ij contains incomes (or losses) from the choice of the strategy u i when implementing the state of nature v j .
It is required to find the optimal strategy.
4.2.1 Wald criterion . In accordance with the criterion Wald (criterion of extreme pessimism) as the optimal strategy is chosen, guaranteeing a gain of no less than the "lower price of the game with nature":
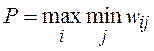 .
.
The decision rule in accordance with the Wald criterion can be interpreted as follows: the decision matrix W is complemented by one more column from the smallest results w ir of each row. Choose the option, in the row of which is the largest value of w ir of this column.
The solution chosen in this way completely eliminates the risk. This means that the decision maker cannot face a worse result than the one he or she focuses on. Whatever conditions v j meet, the corresponding result cannot be lower than P. This property forces to consider the Wald criterion one of the fundamental. Therefore, in technical tasks it is used both consciously and unconsciously. However, in practical situations, the excessive pessimism of this criterion can be very disadvantageous.
The application of this criterion may be justified if the situation in which the decision is made is characterized by the following circumstances:
about the probability of occurrence of the state of nature v j nothing is known;
with the emergence of the state v j must be considered;
only a small number of solutions are implemented;
no risk is allowed.
4.2.2. Bayes-Laplace criterion . The Bayes-Laplace criterion, unlike the Wald criterion, takes into account each of the possible consequences of all solutions:
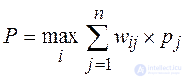 .
.
The corresponding selection rule can be interpreted as follows: the decision matrix W is complemented by one more column containing the expectation of the values of each of the rows. Selects the option in the rows of which is the largest value of w ir of this column.
The Bayes-Laplace criterion makes the following requirements for a situation in which a decision is made:
the probability of occurrence of the state v j is known and does not depend on time;
the decision made theoretically allows for an infinitely large number of realizations;
some risk is allowed with small numbers of implementations.
4.2.3. Savage Criterion . In accordance with the Savage criterion, the optimal strategy is chosen such that the risk value takes the smallest value in the most unfavorable situation :
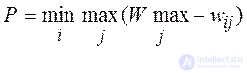 .
.
Here, the value of P can be interpreted as the maximum additional gain, which is achieved if in the state v j instead of the variant u i choose another, optimal for this external state, variant.
The selection rule that meets the Savage criterion is the following: each element of the decision matrix W is subtracted from the highest result 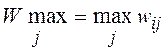 corresponding column. Differences form a matrix of residuals (risks). This matrix is replenished with the column of the largest differences w ir . Selects the option in the row which is the lowest value.
corresponding column. Differences form a matrix of residuals (risks). This matrix is replenished with the column of the largest differences w ir . Selects the option in the row which is the lowest value.
4.3.4. Criterion Hurwitz . According to the Hurwitz criterion a strategy is chosen that takes some intermediate position between extreme pessimism and optimism:
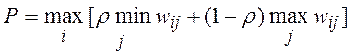 ,
,
Where 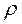 - pessimism coefficient chosen in the interval [ 0,1 ].
- pessimism coefficient chosen in the interval [ 0,1 ].
The selection rule according to this criterion is the following: the solution matrix W ij is supplemented with a column containing the weighted average of the smallest and the greatest results for each row. Select the option in the rows of which are the largest elements of w r this column.
With 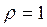 the Hurwitz criterion turns into the Wald criterion (pessimist), and
the Hurwitz criterion turns into the Wald criterion (pessimist), and 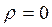 - in the criterion of a gambler. From this it is clear how important the weight factor is.
- in the criterion of a gambler. From this it is clear how important the weight factor is.  . In technical applications, choosing the right factor is as difficult as choosing the right criteria. Therefore, most often a weight factor
. In technical applications, choosing the right factor is as difficult as choosing the right criteria. Therefore, most often a weight factor 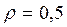 taken as a middle point of view.
taken as a middle point of view.
The Hurwitz criterion makes the following requirements for the situation in which a decision is made:
about the probability of occurrence of the state of nature v j nothing is unknown;
with the emergence of the state v j must be considered;
only a small number of solutions are implemented;
some risk is allowed.
It is difficult to give general recommendations on the choice of one or another criterion. However, we note the following: if in certain situations even minimal risk is not allowed, then the Wald criterion should be applied; if a certain risk is perfectly acceptable, then you can use the Savage criterion. It may be recommended to simultaneously apply alternate criteria. After that, among several options selected in such a way as optimal, it is necessary to select a final decision by will.
Such an approach makes it possible, firstly, to better penetrate into all internal relations of the problem of decision-making and, secondly, to weaken the influence of the subjective factor. In addition, in the field of technical problems, various criteria often lead to the same result.
Example
Justification of the repair crew. The company is resolving the issue of creating a repair crew. Based on the application of the Wald, Laplace, Savage, and Hurwitz criteria, determine the most appropriate number of brigade members. The initial data are summarized in Table 4.1, in the cells of which incomes are entered for different variants (strategies). Under the strategy refers to x - the number of members of the team and R - the number of machines that require repair.
Table4.1
Initial data
|
x \ R |
40 |
thirty |
20 |
ten |
|
five |
50 |
100 |
180 |
250 |
|
four |
80 |
70 |
80 |
230 |
|
3 |
210 |
180 |
120 |
210 |
|
2 |
300 |
220 |
190 |
150 |
1. Wald criterion. On the right is added a column of minima in rows.
|
x \ R |
40 |
thirty |
20 |
ten |
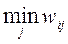 |
|
five |
50 |
100 |
180 |
250 |
50 |
|
four |
80 |
70 |
80 |
230 |
70 |
|
3 |
210 |
180 |
120 |
210 |
120 |
|
2 |
300 |
220 |
190 |
150 |
150 |
Then 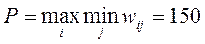 . Thus, under these conditions, the rational solution is x = 2 .
. Thus, under these conditions, the rational solution is x = 2 .
2 Laplace criterion. Consider a situation where all states of nature are equally likely. In this case, the criterion will take the form:
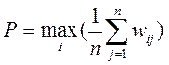
|
x \ R |
40 |
thirty |
20 |
ten |
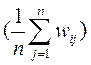 |
|
five |
50 |
100 |
180 |
250 |
145 |
|
four |
80 |
70 |
80 |
230 |
115 |
|
3 |
210 |
180 |
120 |
210 |
180 |
|
2 |
300 |
220 |
190 |
150 |
215 |
Then 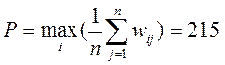 . Thus, the best solution is x = 2 .
. Thus, the best solution is x = 2 .
3. Savage Criterion . Let's build a risk matrix. Its elements are determined by the formula 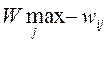 where
where 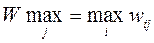 .
.
|
x \ R |
40 |
thirty |
20 |
ten |
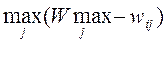 |
|
five |
300-50 = 250 |
120 |
ten |
0 |
250 |
|
four |
220 |
150 |
110 |
20 |
220 |
|
3 |
90 |
40 |
70 |
40 |
90 |
|
2 |
0 |
110 |
100 |
100 |
100 |
|
300 |
220 |
190 |
250 |
|
Then 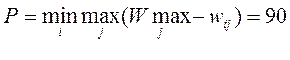 . The optimal strategy according to the Savage criterion is x = 3 .
. The optimal strategy according to the Savage criterion is x = 3 .
4. Hurwitz criterion . In contrast to the “hard” criteria used above, the Hurwitz criterion is “flexible,” since it allows varying the degree of optimism-pessimism. Thus, this criterion establishes a balance between cases of extreme optimism or pessimism, by introducing a coefficient of weight r .
We apply this criterion to our initial data, assuming r = 0.5 .
|
x \ R |
40 |
thirty |
20 |
ten |
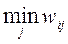 |
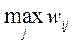 |
P |
|
five |
50 |
100 |
180 |
250 |
50 |
250 |
150 |
|
four |
80 |
70 |
80 |
230 |
70 |
230 |
150 |
|
3 |
210 |
180 |
120 |
210 |
120 |
210 |
165 |
|
2 |
300 |
220 |
190 |
150 |
150 |
300 |
225 |
In this way, 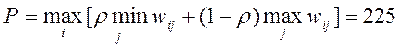 . The optimal strategy is x = 2 .
. The optimal strategy is x = 2 .
Comments
To leave a comment
Decision theory
Terms: Decision theory