2.1 Construction of scales for evaluating criteria

By their nature, the criteria are divided into quantitative and qualitative [5, p. eleven].

A criterion can be considered quantitative if it makes sense to compare its values, indicating how many or how many times one value is greater than another, and qualitative, when such comparisons are meaningless.

An example of a quantitative criterion f _i   is the mass. If a unit of mass measurement is fixed, then we can talk about how much or how much one product is heavier than another: the ratio of the weights of the products does not change after changing to another unit of measurement, that is, after converting   f _i in k * f _i . It is clear that any other transformation can lead to a change in the initial ratio of the values ​​of f _i .

The function φ is called an admissible transformation of the criterion f _i if the function φ ( f _i ) is again a criterion measuring the same property .

A set of permissible transformations Φ is associated with each criterion and it is said that the criterion has a scale of type Φ (Table 1.1).

Table 1.1

Main types of scales

Absolute scale   called a scale of the type F = { φ | φ ( z ) = z }.

Difference scale   called a scale of the type F = { φ | φ ( z ) = z + l } . An example of measurement in this scale is chronology. The transition from one calendar to another is accomplished by changing the reference point.

Scale of relationships   called a scale of the type F = { φ | φ ( z ) = k * z , k> 0} , since the ratios of the quantities k * z ₁ / k * z ₂ = z ₁ / z ₂ = C , where C is const, are preserved. Examples of measurements on this scale are measurements of mass or length.

The scale of intervals is called a scale of the type F = { φ | φ ( z ) = k * z + l , k> 0} . Here, the admissible transformations are multiplication by a positive number k and the addition of an arbitrary number l.

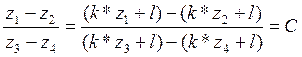where C is const.

An example of a criterion that has a scale of intervals is temperature: for measurement it is necessary to fix the scale and the origin. More often, the criteria are less stringent than the scale of intervals. These scales include all the scales listed below.

The relationship scale is the only scale with a zero point, so it is possible to carry out a quantitative comparison of the results obtained. This addition allows us to talk about the ratio (proportion) a: b for scale values a and b . For example, the respondent may be 2.5 times older, spend three times more money, fly twice as often as compared to another respondent.

An ordinal scale is a scale of the type F = { φ | z ₁ > z ₂ → φ ( z ₁ )> φ ( z ₂ )} .

Criteria having an ordinal scale are called quality criteria .

It makes sense to compare the values ​​of the quality criterion only in terms of “more”, “less” and “equal” relations - they are saved under monotonic transformations. But finding out how many times or how much one value is more than another is meaningless. A criterion with an ordinal scale naturally arises in cases where decisions are ranked. Typically, such rankings are obtained by subjective "measurements", for example, reflect the individual's opinion about the preference of decisions.

The least “strict” type of scale is the nominal scale . The essence of measurement in the nominal scale is the division of alternatives into an equivalence class according to one or another characteristic. An example of a measurement in such a scale is the classification of athletes by grade according to their skill.

Often, subjective measurements are performed in point or verbal-numeric scales . They occupy an intermediate position between quantitative and qualitative.

Verbal-numeric scales are used mainly in cases where the estimates for the criterion are subjective.

For example, the subjective nature, which is based on the experience and knowledge of an expert, carries estimates of the degree of risk, the expected competitiveness of products, the comparative significance of a particular factor, and many others.

The essence of verbal-numerical scales is that they allow to measure the degree of intensity of the criterion property, which has a subjective character.

The composition of verbal-numeric scales includes, as a rule, a meaningful description of grades of the scale and numerical values ​​corresponding to each of the grades of the scale.

As an example of a verbal - numerical scale that has a fairly wide application, we give the Harrington scale, which characterizes the degree of manifestation of the criterion property and has a universal character (Table 1.2).

Table 1.2

Harrington's Verbal Numeric Scale

Note that the numerical values ​​of the Harrington scale are derived from the analysis and processing of a large array of statistical data.

However, when evaluating management decision-making objects on criteria that allow only a subjective assessment of specialists, it is advisable to develop and use special scales reflecting the specifics of a particular criterion of a particular group of objects when making and making a management decision [6].