Lecture
Given:
a 1 , a 2 , ..., a n are alternatives , n is the number of alternatives,
P 1 , P 2 , ... P m - individual rankings of alternatives by experts, m - the number of experts.
Rankings have the form 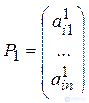 where
where
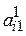 - the alternative that ranks first in the P 1 ranking,
- the alternative that ranks first in the P 1 ranking,
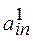 - alternative, standing on the n- th place in the ranking of P 1 .
- alternative, standing on the n- th place in the ranking of P 1 .
Alternative 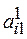 has rank 1, alternative
has rank 1, alternative 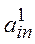 has rank n .
has rank n .
Required to find: final ranking P * , taking into account the opinion of all experts.
According to the majority rule, the number of experts who preferred each of the alternatives is calculated, and the best alternative is announced, which the best experts called the best. Let considered 5 alternatives. Their ranking, corresponding to the opinion of 10 experts, is presented in Table. 5.1:
Table 5.1
An example of ranking alternatives by experts
Expert number 1 | Expert number 2 | Expert number 3 | Expert number 4 | Expert number 5 | Expert number 6 | Expert number 7 | Expert number 8 | Expert number 9 | Expert number 10 |
A1 | A1 | A1 | A4 | A3 | A5 | A2 | A3 | A4 | A5 |
A2 | A2 | A5 | A2 | A2 | A4 | A4 | A2 | A2 | A2 |
A5 | A5 | A3 | A5 | A5 | A2 | A3 | A4 | A5 | A4 |
A3 | A4 | A4 | A3 | A4 | A3 | A5 | A5 | A3 | A3 |
A4 | A3 | A2 | A1 | A1 | A1 | A1 | A1 | A1 | A1 |
In this case, according to the majority rule, the alternative A 1 will be better, since it was called the best 3 experts (for the remaining alternatives, this number is less than or equal to 2). However, the same alternative was recognized as the worst by 7 out of 10 experts. So the recognition of the alternative A 1 best is debatable. To eliminate such shortcomings introduce additional requirements. For example, only the alternative that is considered better by at least half of the experts can become better. Under such conditions, there may not be a better alternative at all.
Condorcet was offered the following case to determine the best alternative. Each expert ranks the alternatives by preference. Based on the obtained rankings for each pair of alternatives, A i and A j are calculated S ij is the number of experts who consider A i to be more preferable than A j . If S ij > S ji , then the alternative A i is considered more preferable than A j . The best alternative is declared A i if S ij > S ji for all i ≠ j . In this case, the alternative to Condorcet is the alternative to A 2 . However, using the Condorcet principle, a paradox may arise that is a consequence of the intransitivity of collective relations. If the three experts ranked the alternatives A 1, A2, A3 as follows:
A1 A3 A2
A2 A1 A3
A3 A2 A1
then S 12 > S 21 , S 23 > S 32 , S 31 > S 13 . There is no alternative to Condorcet.
The Borda method is based on ordering alternatives based on the sum of ranks assigned to alternatives by experts [6, p. 62]. The alternatives ranked by the experts are assigned the number: the last one by preference - 0, the penultimate one - 1, etc. The method consists of 2 stages:
1. At the first stage, for each object with number k , the value of S k is determined, equal to the sum of ranks assigned to the object by all experts:
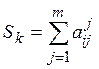 ;
;
2. at the second stage, the object's rank is determined - the larger the value of S k , the higher the place of the alternative in the sought ranking.
An example of constructing a final ranking using the method of bord
Let there be alternatives a 1 , a 2 , a 3 , a 4 and the ranking of these alternatives by experts (Table 5.2). Required to find the final ranking.
Table 5.2
Ranking criteria by experts
P 1 | a 3 | P 2 | a 2 | P 3 | a 1 | P 4 | a 4 |
a 2 | a 3, | a 3 , a 4 | a 3 | ||||
a 4 | a 4 | a 2 | a 1 , a 2 | ||||
a 1 | a 1 |
Denote the R 1 ranks obtained on the basis of alternative rankings by experts, R2 , R 3 , R 4. The process of constructing the final ranking using the Bord method is presented in Table. 5.3.
Table 5.3
Building a final ranking
Alternative | R 1 | R 2 | R 3 | R 4 | Sum of ranks S k | Place in the final ranking |
a 1 | 0 | 0 | 2 | 0 | 2 | 3 |
a 2 | 2 | 3 | 0 | 0 | five | 2 |
a 3 | 3 | 2 | one | one | 7 | one |
a 4 | one | one | one | 2 | five | 2 |
The Kemeny median search method allows finding the final ranking P , the total distance from which to all given rankings is minimal:
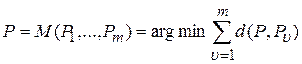 ,
,
where m is the number of experts, P 1 , ..., P m are the rankings, d (P, P u ) is the distance between the rankings [6, p. 73].
Thus, to search for a median, it is necessary to introduce the concept of the distance between rankings . It is defined using the relationship matrix. 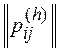 ,
, 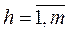 ,
, 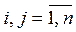 , n is the number of alternatives.
, n is the number of alternatives.
r i , r j are the ranks of the i -th and j -th alternatives in the ranking of the hth expert. Note that alternative ranks are compared the other way round, that is, the rank is r i = 1> r j = 2 (rank 1 is greater than rank 2 ) and r i = 5 < r j = 3 (rank 5 is less than rank 3 ).
Distance from arbitrary ranking P , which corresponds to the matrix, to all rankings P 1 , P 2 , ..., P m , which correspond to the matrix of pair relations 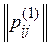 , ...,
, ..., 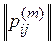 is determined by the formula:
is determined by the formula:
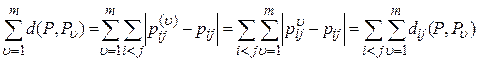 .
.
To find the Kemeny median, a loss matrix is introduced. 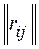 ,
, 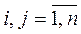 .
.
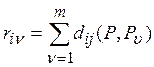 ,
,
where P is the ranking, the element of the matrix of relations p ij is equal to 1 .
At the same time, the task of finding the Kemeny median for rankings is formulated as the task of finding such an ordering of alternatives, and therefore rows and columns of the loss matrix, so that the sum of its elements located above the diagonal is minimal.
Kemeny median heuristic search algorithm
Suppose that for the initial rankings the loss matrix is defined. The search process for the final ranking consists of 2 stages.
At the first stage, a preliminary ranking of P I is built .
1st iteration . Calculate the sum of the elements of the rows of the loss matrix:
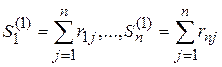 .
.
Find the minimum of them.  .
.
Alternative a i1 , put in first place in the desired ranking. Striking out in 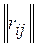 row and column with number i 1 , we get a matrix, the set of indices of rows and columns, respectively, I (1) = J (1) = {1, ..., n } \ I 1 .
row and column with number i 1 , we get a matrix, the set of indices of rows and columns, respectively, I (1) = J (1) = {1, ..., n } \ I 1 .
kth iteration . In the loss matrix 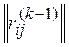 calculate the sum of the elements of the lines:
calculate the sum of the elements of the lines:
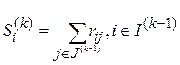 .
.
Find the minimum of them:
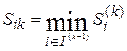 .
.
Alternative a ik , put on the k - th place in the desired ordering. Striking out in 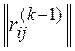 row and column with number i k , we get the matrix
row and column with number i k , we get the matrix 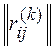 , the set of indices of rows and columns, respectively, I ( k ) = J ( k ) = {1, ..., n } \ { i 1 , ..., i k } .
, the set of indices of rows and columns, respectively, I ( k ) = J ( k ) = {1, ..., n } \ { i 1 , ..., i k } .
The algorithm terminates after the nth iteration ( I ( k ) = J ( k ) and is equal to the empty set). Sought ordering
In the second stage of the found ranking P I get the final ranking of P II , with the process of transition from ranking P I to ranking P II happens as follows: for the ranking elements P I, we successively verify the validity of relations (1)
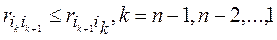 (5.1)
(5.1)
Once for some k it is broken, the alternatives a ik and a ik +1 in the ranking are interchanged, and we check the relation (5.1), starting with the alternative immediately preceding the alternative subjected to the permutation. After a finite number of steps, a P II ranking will be obtained.
An example of constructing a final ranking using the Kemeny median search method
Consider the process of constructing the final ranking on the example discussed earlier (the initial data are presented in Table 5.2).
1. Build a matrix of relations for the ranking of experts:
| 0 | -one | -one | -one | 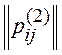 | 0 | -one | -one | -one |
one | 0 | -one | one | one | 0 | one | one | ||
one | one | 0 | one | one | -one | 0 | one | ||
one | -one | -one | 0 | one | -one | -one | 0 | ||
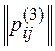 | 0 | one | one | one | 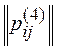 | 0 | 0 | -one | -one |
-one | 0 | -one | -one | 0 | 0 | -one | -one | ||
-one | one | 0 | 0 | one | one | 0 | -one | ||
-one | one | 0 | 0 | one | one | one | 0 |
For example, p 12 (1) = -1 , since r 1 < r 2 ( r 1 = 3, r 2 = 1 ), p 34 (2) = 0 , because r 3 = r 4 ( r 3 = 2 r 4 = 2 ).
2. The loss matrix has the following form:
0 | five | 6 | 6 |
3 | 0 | 6 | four |
2 | 2 | 0 | 3 |
2 | four | five | 0 |
For example, r 12 = d 12 ( P 1 , P 3 ) + d 12 ( P 2 , P 3 ) + d 12 ( P 4 , P 3 ) , since P 3 is a ranking, the element of the relationship matrix is p 12 (3 ) = 1 . Then r 12 = | p 12 (3) - p 12 (1) | + | p 12 (2) - p 12 (3) | + | p 12 (3) - p 12 (4) | = | 1 - (- 1) | + | 1 - (- 1) | + | 1-0 | = 5 .
3. Find a preliminary ranking of P I ( first stage ).
1st iteration . Calculate
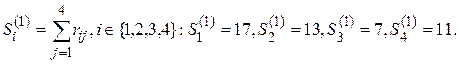
The minimum is reached at S 3 (1) . In first place in the ranking P I alternative a 3 is placed, and it is excluded from further consideration.
2nd iteration . Calculate 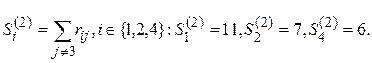
The minimum is reached at S 4 (2) . The second place in the P I ranking is the alternative to a 4 , and it is excluded from further consideration.
3rd iteration . Calculate 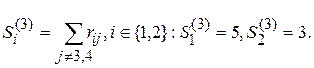
The minimum is reached on S 2 (3) . The third place in the P I ranking is the alternative to a 2 , and it is excluded from further consideration. Thus, the P I ranking is as follows:
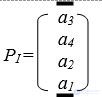
4. Find the P II ranking ( second stage ).
So, i 1 = 3, i 2 = 4, i 3 = 2, i 4 = 1. Compare 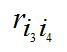 and
and 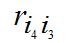 or r 21 and r 12 , Since r 21 ≤ r 12 ( 3 ≤ 5 ), the alternatives are not interchanged, go to the comparison of r 42 and r 24 . Since r 42 ≤ r 24 ( 4 ≤ 4 ) , we turn to the comparison of r 34 and r 43 . Since r 34 < r 43 ( 3 ≤ 5 ), then the found ranking
or r 21 and r 12 , Since r 21 ≤ r 12 ( 3 ≤ 5 ), the alternatives are not interchanged, go to the comparison of r 42 and r 24 . Since r 42 ≤ r 24 ( 4 ≤ 4 ) , we turn to the comparison of r 34 and r 43 . Since r 34 < r 43 ( 3 ≤ 5 ), then the found ranking

and is a P II ranking for which relations (5.1) are satisfied.
The final rankings of alternatives by the Board method and the Kemeny median search method are presented in Table. 5.5.
Table 5.5
The results of the construction of the final ranking using the method of the Board and the method of searching for the Kemeny median
Alternative | Place in the final ranking (Kemeny) | Place in the final ranking (Bord) |
a 1 | four | 3 |
a 2 | 2 | four |
a 3 | one | one |
a 4 | 3 | 2 |
The results of the work of the methods described above can sometimes vary quite strongly. The Borda method gives results that are intuitive, since it is based on the idea of averaging estimates. As for the method of searching for the Kemeny median, then, on the contrary, it can give unexpected results. To obtain the final ranking, the method uses a special estimate — the distance between the rankings. And the algorithm for obtaining the final ranking considered by us is based on heuristics — the assumption that the final ranking constructed in this way will be closest to the opinion of all experts from the point of view of the estimate introduced.
Comments
To leave a comment
Decision theory
Terms: Decision theory