7.6. GSM mobile cellular network capacity

When designing cellular mobile communication networks, it is necessary to estimate the traffic (load intensity) of the communication system, which in turn makes it possible to estimate the number of subscribers in a cell and in the network as a whole. In this connection, a cellular mobile communication system, like any telephone communication system, is an example of a queuing system with a random flow of calls (calls), a random duration of their service and a finite number of service channels (namely, physical radio channels). Taking advantage of the well-developed theory of teletraffic in telephony, we apply it to the cellular mobile communication system.

Consider the basic values ​​needed to build mathematical traffic models:

- average frequency of incoming calls (k), measured by the number of calls per unit of time ([k] = call / h, call / s); the call flow can be adequately characterized by the average frequency of incoming calls (intensity of incoming calls) X;

- the average duration of service of one call (the average duration of one call) (7), measured in units of time;

- average load intensity (traffic intensity), equal to the product

A = measured in Erlang (Earl). (7.15)

Consider the following example. Let the average frequency of incoming calls (k) = 20 calls / hour, and the average service time per call (G) = 0.2 hours, then the average traffic intensity is A = 20 * 0.2 = 4 Erlang, that is, the average load intensity equals 4 challenges. Typically, the value of average traffic A is estimated for peak hours, that is, for the hourly interval during the period of the highest load of the communication system.

Probability Characteristics in Teletraffic Theory

Arrival of calls, as well as the duration of service T (t), are random variables depending on time. Probability theory can be used to derive relations that establish a connection between three factors: the expected load; number of channels; indicator of quality of service.

The probability of receiving calls can be described by the Poisson distribution, which determines the probability of receiving ^ -calls (discrete random variable) during time t:

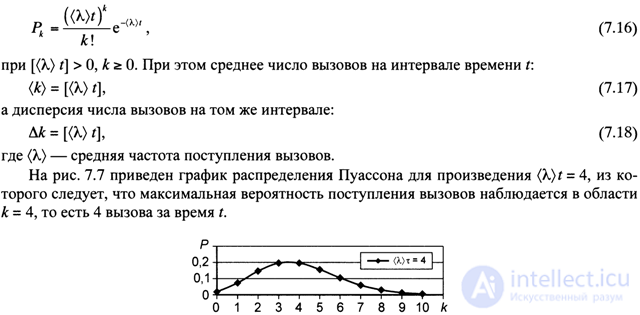
The duration of a single call service (the duration of a communication channel's employment) is a continuous random variable x (t \, whose probability distribution density is described by the exponential distribution law:

Mathematical models in cellular mobile communication systems.

In mathematical traffic models, as shown in [7.1], the following conditions are true:

- the call flow is subject to the Poisson distribution;

- call service duration is subject to exponential distribution, with different models differing from one another in what fate befalls calls arriving at times when all channels of the system are busy.

These calls can be canceled (model of the system with refusals), or stand in a queue and wait for the channel to be released indefinitely, and then serviced for the required time interval (model of the system with waiting);

- intermediate cases are possible, for example, models with expectation, but for limited time intervals.

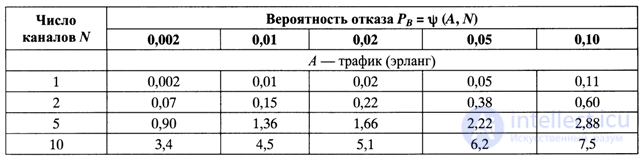
The model of a system with refusals (lost-calls-cleared conditions - conditions for dropping calls that were refused) is also called the Erlang model B. In this model, the probability of failure (that is, the probability of incoming calls at the time when all channels are busy) is defined by the expression:

where N is the number of channels, A = (X,) * (I) is traffic.

The probability that all channels are free for this model is determined by the expression:

The model of a system with expectation is called the Erlang S. model.

In this model, the probability of a delay (that is, the probability that an incoming call is not served immediately, but becomes a queue) is determined by the formula:

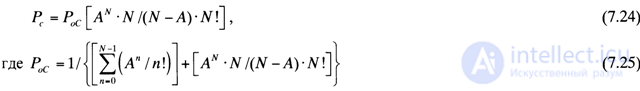
the probability that all channels are free.

Model of a system with a limited waiting time, the so-called Erlang A model or the Poisson model. In this model, the call received at the time of the employment of all channels becomes in the queue, but the waiting time does not exceed the average service time (average call duration). If during this time at least one channel is released, the call takes it to the vacated part of the average service time, and then is dropped. In such a system, the probability of failure:

When calculating the capacity of cellular mobile communication systems, the Erlang B model is usually used. This is because with small probabilities of failure, the Erlang models B and C give fairly close results, while with a probability of failure Pv> 0.1, a relatively small increase in traffic (A> 40) leads to a sharp increase in the probability of failure, that is, to a sharp deterioration in the quality of service. Therefore, the calculation of the capacity of a cellular mobile communication system is carried out for Pb values ​​ranging from 0.01 to 0.05.

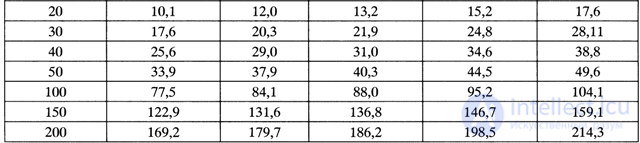
In view of the bulkiness of expression (7.20), which determines the probability of blocking a call in a system with refusals, in practice it is usually used to present it in the form of a table. 7.1 [7.4, 7.5].

Table 7.1. Erlang B model (system with failures)

Methods of using the Erlang B model for calculating the capacity of a cellular system.

Formulation of the problem. Calculate the capacity of a cellular mobile system (capacity of one cell and the entire cellular network) for given: probabilities of failure Pb, number of channels N and number of hundred tons.

The solution of the problem.

1. Since the function PB = ty (A, N) depends on the traffic L and the number of channels N, then with two known parameters there is always a third one: if, for example, PB (or selected) and N are known, then there will be a value L.

2. After determining the amount of traffic A by the formula (7.20) or from table. 7.1 (after assessing the number of calls of subscribers of the cellular network on average per hour (X \), as well as the average duration of a call (Ti)), the number of subscribers in one cell is calculated:

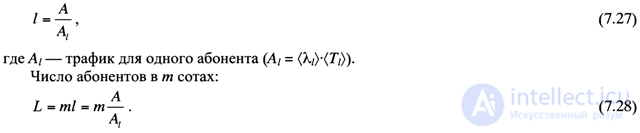
Consider a numerical example.

Formulation of the problem. Let the cellular mobile communication system consist of 51 cells, each of which uses N physical channels. Let the probability of failure (for the Erlang model B) Pb = 0.05. Suppose that during the operation of the GSM network, during peak hours, each subscriber makes an average of one call per hour, that is, (k \) = 1 call / hour. Let the average call duration of subscribers (T \) is 2 minutes, that is (T) / 1 h = 1/30 hours. In this case, the traffic of one conversation will be: At = (ki) - (Ti) = 1-1 / 30 = 0.033 Earl.

The solution of the problem.

1. With the probability of failure Pb = 0.05 in accordance with the table. 7.1 when the number of channels per cell ps = 20, the value of traffic per cell will be Ac = 15.2 Earl / cell.

2. The number of subscribers that can be served within one cell, equal to the ratio of traffic per cell to traffic per subscriber, will be: mt - AJAi = 15.2 / 0.033 = 460 subscribers.

3. The number of M subscribers serviced by the whole set of 51 cells, with the number of channels N = 20: M = 51-460 = 23490.

Such is the capacity of the considered cellular mobile communication system, calculated in accordance with the generally accepted approach for the peak hour according to the Erlang W model. Thus, in p. 7.3-7.6 were considered approximate methods used in the design of cellular mobile communication systems:

- radio coverage of the service area;

- distribution of radio frequency channels;

- calculation of the budget of radio lines;

- calculation of network capacity.

For greater completeness of the presentation of this problem, we use the recommendations of the company Nokia for the design of cellular networks, described in [7.9].